专题03 平面向量的综合应用（知识串讲+热考题型+专题训练）-2022-2023学年高一数学下学期期中期末考点大串讲（人教A版2019必修第二册）

这是一份专题03 平面向量的综合应用（知识串讲+热考题型+专题训练）-2022-2023学年高一数学下学期期中期末考点大串讲（人教A版2019必修第二册），文件包含专题03平面向量的综合应用解析版docx、专题03平面向量的综合应用原卷版docx等2份试卷配套教学资源，其中试卷共56页， 欢迎下载使用。

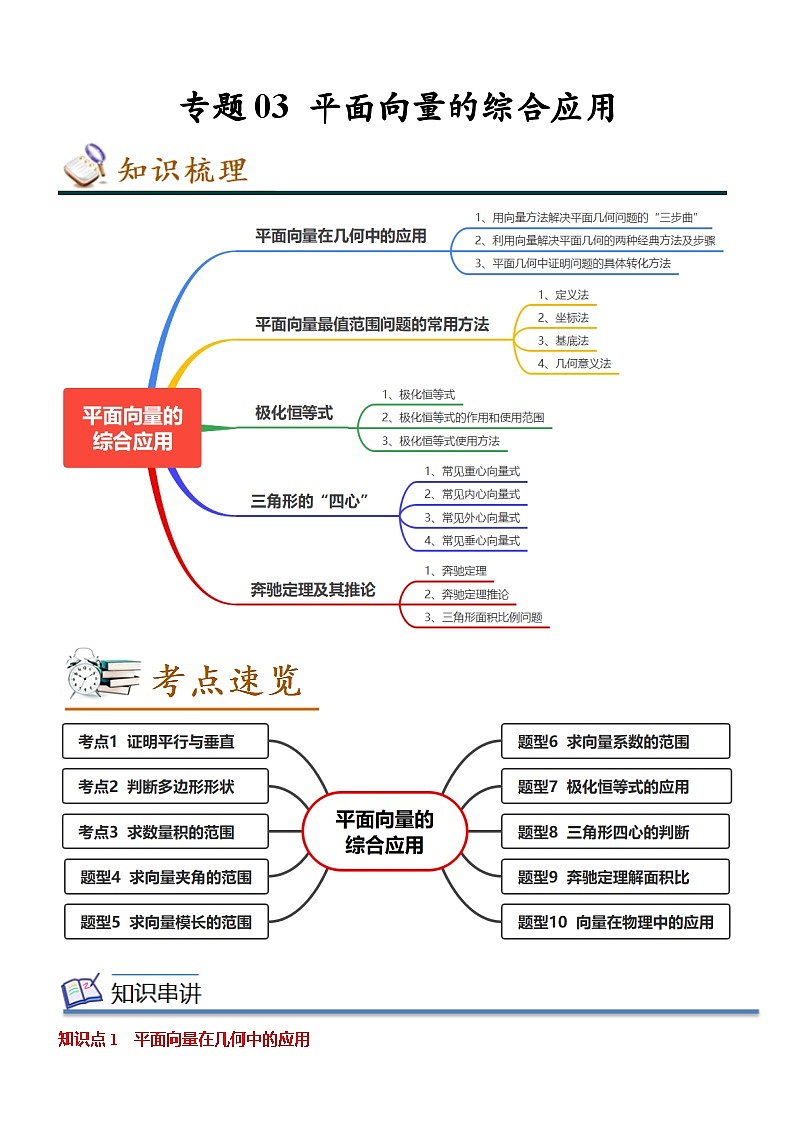
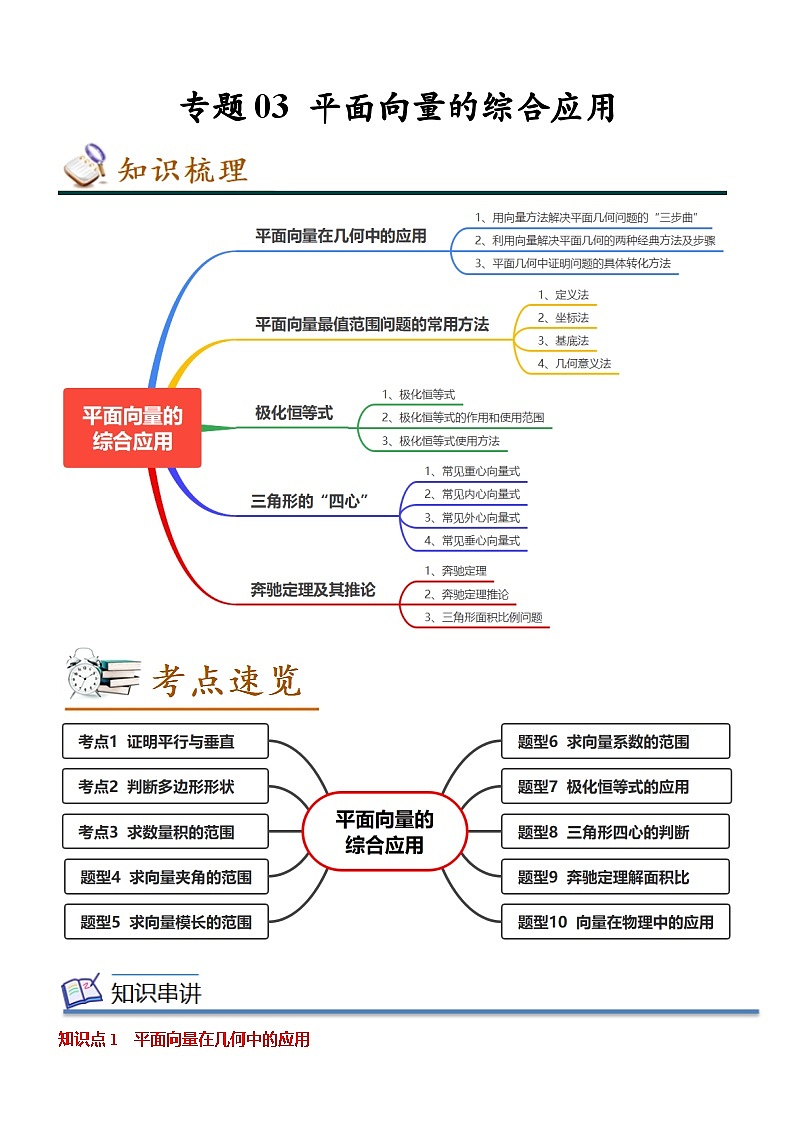
专题03 平面向量的综合应用






知识点1 平面向量在几何中的应用
1、用向量方法解决平面几何问题的“三步曲”：
（1）建立平面几何与向量的关系，用向量表示问题中涉及到的几何元素，将平面几何问题转化为向量问题；
（2）通过向量运算，研究元素之间的关系，如距离、夹角等问题；
（3）把运算结果“翻译”成几何关系。
2、利用向量解决平面几何的两种经典方法及步骤：
线性运算法
（1）选取合适的基底（一般选择夹角和模长已知的两个向量）；
（2）利用基底表示相关向量；
（3）利用向量的线性运算或数量积找到相应关系；
（4）把计算结果“翻译”为几何问题。
坐标运算法
（1）建立适当的直角坐标系（尽可能让更多的点在坐标系上）；
（2）把相关向量坐标化；
（3）用向量的坐标运算找到相应关系；
（4）利用向量关系回答几何问题。
3、平面几何中证明问题的具体转化方法
（1）证明线段，可转化为证明；
（2）证明线段，只需证明存在一个实数，使成立；
（3）证明两线段，只需证明数量积；
（4）证明三点共线，只需证明存在一个，使成立。
知识点2 平面向量最值范围问题的常用方法
1、定义法
第1步：利用向量的概念及其基本运算将所求的问题转化为相应的等式关系；
第2步：运用基本不等式求其最值问题；
第3步：得出结论。
2、坐标法
第1步：根据题意建立适当的直角坐标系，并推导关键点的坐标；
第2步：将平面向量的运算坐标化；
第3步：运用适当的数学方法如二次函数、基本不等式的思想、三角函数思想等求解。
3、基底法
第1步：利用基底转化向量；
第2步：根据向量运算化简目标；
第3步：运用适当的数学方法如二次函数、基本不等式的思想、三角函数等得出结论；
4、几何意义法
第1步：结合条件进行向量关系推导；
第2步：利用向量之间的关系确定向量所表达的点的轨迹；
第3步：结合图形，确定临界位置的动态分析求出范围。
知识点3 极化恒等式
1、极化恒等式：
（1）平行四边形模式：如下图，平行四边形ABCD，O是对角线交点．则·＝[|AC|2－|BD|2]．

（2）三角形模式：如上图，在△ABC中，设D为BC的中点，则·＝|AD|2－|BD|2．
2、极化恒等式的作用和使用范围
（1）极化恒等式的作用：
建立了向量的数量积与几何长度(数量)之间的桥梁，实现向量与几何、代数之间的互相转化。
（2）极化恒等式的适用范围：
共起点或共终点的两向量的数量积问题可直接进行转化；不共起点和不共终点的数量积问题
可通过向量的平移，等价转化为共起点或共终点的两向量的数量积问题。
3、极化恒等式使用方法
在确定求数量积的两个向量共起点或共终点的情况下，极化恒等式的一般步骤如下：
第一步：取第三边的中点，连接向量的起点与中点；
第二步：利用极化恒等式公式，将数量积转化为中线长与第三边长的一半的平方差；
第三步：利用平面几何方法或用正余弦定理求中线及第三边的长度，从而求出数量积，
如需进一步求数量积范围，可以用点到直线的距离最小
或用三角形两边之和大于等于第三边，两边之差小于第三边
或用基本不等式等求得中线长的最值(范围)。
知识点4 三角形的四心
1、常见重心向量式：设O是∆ABC的重心，P为平面内任意一点
（1）
（2）
（3）若或，，则P一定经过三角形的重心
（4）若或，λ∈[0,+∞)，则P一定经过三角形的重心
2、常见内心向量式：P是∆ABC的内心，
（1）ABPC+BCPA+CAPB=0（或aPA+bPB+cPC=0）
其中a，b，c分别是∆ABC的三边BC、AC、AB的长，
（2）AP=λABAB+ACAC，λ[0,+∞)，则P一定经过三角形的内心。
3、常用外心向量式：O是∆ABC的外心，
（1）OA=OB=OC⟺OA2=OB2=OC2
（2）OA+OB∙AB=OB+OC∙BC=OA+OC∙AC=0
（3）动点P满足OP=OB+OC2+λABABcosB+ACACcosC，λ∈0,+∞，
则动点P的轨迹一定通过∆ABC的外心.
（4）若OA+OB∙AB=OB+OC∙BC=OC+OA∙CA=0，则O是∆ABC的外心.
4、常见垂心向量式：O是∆ABC的垂心，则有以下结论
（1）OA∙OB=OB∙OC=OC∙OA
（2）OA2+BC2=OB2+CA2=OC2+AB2
（3）动点P满足，λ∈0,+∞，则动点P的轨迹一定过∆ABC的垂心
（4）奔驰定理推论S∆BOC:S∆COA:S∆AOB=tanA:tanB:tanC，tanA∙OA+tanB∙OB+tanC∙OC=0.
知识点5 奔驰定理及其推论
1、奔驰定理：O是内的一点，且，则
2、奔驰定理推论：，则
①
②，，.
由于这个定理对应的图象和奔驰车的标志很相似，我们把它称为“奔驰定理”．
3、对于三角形面积比例问题，常规的作法一般是通过向量线性运算转化出三角形之间的关系。但如果向量关系符合奔驰定理的形式，在选择填空题当中可以迅速的地得出正确答案。

考点1 证明平行与垂直

【例1】（2023春·全国·高一专题练习）在中，点，分别在线段，上，，.求证：.
【答案】证明见解析
【解析】证明：设，，则.
又，.所以，.
在中，，
所以，即与共线，故.


【变式1-1】（2023春·山东济南·高一山东师范大学附中校考阶段练习）在平面直角坐标系中，的三个顶点坐标分别为，，(且)，D为AB的中点，E为的重心，F为的外心．
（1）求重心E的坐标；
（2）用向量法证明：．
【答案】（1）；（2）证明见解析
【解析】（1）如图，

∵，，，
∴，则由重心坐标公式，得；
（2）．
易知的外心F在y轴上，可设为．
由，得，
∴，即．∴．
∴，
∴，即．


【变式1-2】（2023·高一课时练习）在中，，分别为边上的点，且．求证：．

【答案】证明见解析.
【解析】因为，
．
由且，
得，
所以.


【变式1-3】（2020·高一课时练习）如图，在正方形中，为对角线上任意一点（异于、两点），，，垂足分别为、，连接、，求证：.

【答案】见解析
【解析】设正方形的边长为，，
则，，.，

，
，即.


考点2 判断多边形形状

【例2】（2023春·北京顺义·高一北京市顺义区第一中学校考阶段练习）是所在平面内一点，满足，则的形状是（ ）
A．等边三角形 B．锐角三角形 C．直角三角形 D．钝角三角形
【答案】C
【解析】因为，
由可得，
可得，整理可得，，
所以，为直角三角形.故选：C.


【变式2-1】（2023·全国·高一专题练习）在四边形ABCD中，若，则该四边形为（ ）
A．平行四边形 B．矩形 C．等腰梯形 D．菱形
【答案】B
【解析】由得，所以，∥，
所以四边形ABCD为平行四边形，
又，所以．所以四边形ABCD为矩形，故选：B


【变式2-2】（2021春·天津西青·高一统考期末）已知非零向量与满足，且，则为（ ）
A．等腰非等边三角形 B．等边三角形
C．三边均不相等的三角形 D．直角三角形
【答案】A
【解析】都为单位向量，所以在的角平分线上，
由，得,由，得，
所以为等腰非等边三角形，故选：A


【变式2-3】（2023·全国·高一专题练习）（多选）在△ABC中，下列正确的是（ ）
A．若，则△ABC为钝角三角形
B．若，则△ABC为直角三角形
C．若，则△ABC为等腰三角形
D．已知，且，则△ABC为等边三角形
【答案】BCD
【解析】对A，即，即，可得，
不能证明△ABC为钝角三角形，故A错误；
对B，即，
解得，故，故B正确；
对C，若，则，故，
故△ABC为等腰三角形，故C正确；
对D，因为，故，即，
又，所以，故，故
同理，结合可得，
故△ABC为等边三角形，故D正确；故选：BCD


【变式2-4】（2023春·全国·高一专题练习）已知四边形ABCD的四个顶点分别为，，，．
（1）求向量与夹角的余弦值；
（2）证明：四边形ABCD是等腰梯形．
【答案】（1）；（2）证明见解析.
【解析】（1）因为，，
所以．
（2）因为，所以，即，
而，，
故不存在使，即不平行，
又，，故，
综上，四边形ABCD是等腰梯形．


考点3 求数量积的范围

【例3】（2023·全国·高一专题练习）四边形ABCD中，，，，则的最小值为（ ）
A． B． C．3 D．－3
【答案】D
【解析】延长交于，因为，，
∴，为等边三角形，
设，则，
∴，
所以当时，的最小值为.故选：D.


【变式3-1】（2022春·重庆·高一校联考阶段练习）若中，，其重心满足条件：，则取值范围为（ ）
A． B． C． D．
【答案】D
【解析】如图所示：因为，为重心，且，
所以，又，则，
在中，有，
在中，有，
两式相加得，
在中，，且，
所以.故选：D


【变式3-2】（2023春·河南·高一河南省实验中学校考阶段练习）已知正六边形ABCDEF的边长为2，P是正六边形ABCDEF边上任意一点，则的最大值为（ ）
A．13 B．12 C．8 D．
【答案】B
【解析】以正六边形ABCDEF中心O为原点建立平面直角坐标系如图，AB、DE交y轴于G、H，
则，
设，，
由正六边形对称性，不妨只研究y轴左半部分，
（1）当P在EH上时，则，，则；
（2）当P在AG上时，则，，则；
（3）当P在EF上时，则：，，
则；
（4）当P在AF上时，则：，，
则.
综上，所求最大值为12.故选：B.


【变式3-3】（2023·全国·高一专题练习）如图，单位向量，的夹角为，点在以为圆心，1为半径的弧上运动，则的最小值为______．

【答案】
【解析】以为坐标原点，分别以为轴，建立空间直角坐标系，
则，设，，
故
，
因为，所以，
故当，时，取得最小值，最小值为.
故答案为：


【变式3-4】（2023·山东泰安·统考一模）如图，在等边三角形ABC中，，点N为AC的中点，点M是边CB（包括端点）上的一个动点，则的最大值为___________.

【答案】3
【解析】以AB中点为原点，边所在的直线为轴，边的垂直平分线为轴，
建立直角坐标系，则，，，AC中点.

设，则，，.
∵在直线上，∴，
∴，
∵，∴当时，的最大值为3.
故答案为：3.


考点4 求向量夹角的范围

【例4】（2023春·天津和平·高一校考阶段练习）已知，若与的夹角为钝角，则实数λ的取值范围为___________.
【答案】且
【解析】若与的夹角为钝角，则，且与不共线，
即，得且.
故答案为：且.


【变式4-1】（2023春·重庆万州·高一重庆市万州第二高级中学校考阶段练习）若平面向量，，满足，，，，则，夹角的取值范围是（ ）
A． B． C． D．
【答案】C
【解析】设，，，以O为原点，方向为x轴正方向建立平面直角坐标系，
，，，
，，三者直接各自的夹角都为锐角，
，，，
，，即在上的投影为1，在上的投影为3，
，，如图

，
即，且
则，
由基本不等式得，，
与的夹角为锐角，，
由余弦函数可得：与夹角的取值范围是，故选：C.


【变式4-2】（2023春·安徽淮南·高一淮南第一中学校联考阶段练习）已知是单位向量，且的夹角为，若，则的取值范围为（ ）
A． B． C． D．
【答案】C
【解析】因为是单位向量，且的夹角为，
所以，
又，所以，
又，所以，所以.故选：C.


【变式4-3】（2023·全国·高一专题练习）已知与为相反向量，若，，则，夹角的余弦的最小值为______．
【答案】-1
【解析】，故，
因为，所以，又，
所以，解得：，
不妨设，，夹角为，则，
两边平方得：，
即，解得：，
因为，所以，
故，夹角的余弦的最小值为-1.


【变式4-4】（2022春·山东泰安·高一统考期中）已知，，为平面向量，，，，.
（1）求的取值范围；
（2）设与的夹角为，求的最小值.
【答案】（1）；（2）.
【解析】（1）因为，所以，
因为，所以，
设与的夹角为，
由上式可得.
又，所以.
令，与的夹角为，
所以，所以.
因为，所以，解得.
综上可得，即；
（2）因为，
所以由（1）可知：当时，的值最小，
代入，得：，
所以的最小值等于.


考点5 求向量模长的范围

【例5】（2022春·北京大兴·高一统考期末）已知向量满足，且，则的取值范围是（ ）
A． B． C． D．
【答案】B
【解析】因为，
向量满足，且，所以，
则，所以.故选：B.


【变式5-1】（2023·全国·高三专题练习）已知向量满足与的夹角为，则当实数变化时，的最小值为___________．
【答案】
【解析】如图，设，
当时，取得最小值，
过B作，即取得最小值为，
因为与的夹角为，
所以，所以．


【变式5-2】（2023秋·浙江宁波·高三期末）若单位向量满足，向量满足，则（ ）.
A． B． C． D．
【答案】C
【解析】令，
不妨，所以中点坐标为，
因为，所以C在以为直径的圆上，即，
所以，
令，
则
，
因为，
所以，
所以.故选：C.


【变式5-3】（2023春·福建三明·高一校考阶段练习）已知点是所在平面内的动点，且满足，射线与边交于点，若，，则的最小值为（ ）
A． B．2 C． D．
【答案】C
【解析】表示与共线的单位向量，表示与共线的单位向量，
的分向与的平分线一致，
，
所以点在的平分线上，即为的角平分线，
在中，，，利用正弦定理知：
同理，在中，
，其中
分析可知当时，取得最小值，即故选：C


【变式5-4】（2022春·贵州黔东南·高一统考期末）已知平面向量满足，，且，若向量，的夹角为60°，则的最大值是________
【答案】
【解析】设，，，由，，且，
可得，，
因为向量，的夹角为60°，即，
所以点C在优弧上运动，故的最大值是的外接圆的直径，
可算得，
由正弦定理，直径．故的最大值是



考点6 求向量系数的范围
【例6】（2022春·吉林长春·高一校考期中）在中，的交点为，过作动直线分别交线段于两点，若，则的最小值为_____.
【答案】
【解析】如图：由三点共线，可得存在实数，使得，
由三点共线，可得存在实数，使得，
所以，解得，
所以，
因为三点共线，所以存在实数，
使得，
所以，所以，
所以，
当且仅当，时，取等号.


【变式6-1】（2022·高一单元测试）在中，，，，是的外接圆上的一点，若，则的最小值是（ ）
A． B． C． D．
【答案】B
【解析】由余弦定理得，、
所以，所以，所以．
以AC的中点为原点，建立如图所示的平面直角坐标系，

易得A（－1，0），C（1，0），B（－，），
设P的坐标为，所以，，，
又，所以，
所以，，
所以，
当且仅当时，等号成立．故选：B．


【变式6-2】（2023春·全国·高一专题练习）在中，CA＝CB＝1，，若CM与线段AB交于点P，且满足，（,），且，则的最大值为______．
【答案】2
【解析】如图所示：

设，，因为，CB＝1，则，
，，设，则，
因为，所以，
因为，则，所以有，
即，即，
又（,），所以，
解得，当且仅当时不等式取等号.
则的最大值为2.


【变式6-3】（2022·高一单元测试）如图，在中，，，，若延长CB到点D，使，当点E在线段AB上移动时，设，当取最大值时，的值是___________.

【答案】
【解析】，
，
所以，所以，
又，所以，，
设，由于在上，所以，
又，
即，化简得，
由得，所以，
（），所以，
所以时，，．


【变式6-4】（2022春·河南郑州·高一校联考期中）在△ABC中，D为边AC上的一点，且，P为边BD上的一点，且满足（、），则下列结论正确的（ ）
A．m＋n＝1
B．mn的最大值为
C．上的最小值为7
D．的最小值为
【答案】D
【解析】因为P为边BD上的一点，所以，
因为，所以，
因为，所以，得，所以A错误，
对于B，因为、，，所以，所以，
当且仅当，即时，取等号，所以的最大值为，所以B错误，
对于C，因为,,，所以，
当且仅当时，取等号，所以的最小值为，所以C错误，
对于D， ，所以，
所以当时，的最小值为，所以D正确，故选：D


考点7 极化恒等式的应用
【例7】（2023春·江苏徐州·高一校考阶段练习）阅读一下一段文字：，，两式相减得 我们把这个等式称作“极化恒等式”，它实现了在没有夹角的参与下将两个向量的数量积运算化为“模”的运算．试根据上面的内容解决以下问题：如图，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点．

（1）若AD＝6，BC＝4，求的值；
（2）若，，求的值．
【答案】（1）；（2）
【解析】（1）
（2）设
，由（1）知 ，即 ①
,同理可得 ，即 ②
由①②解得



【变式7-1】（2023春·安徽安庆·高一安庆一中校考阶段练习）如图，BC，DE是半径为1的圆O的两条直径，F为直径BC上一点，且＝2，则·＝________.

【答案】
【解析】由题意知，，且.
又由知，，
所以

【变式7-2】（2023春·浙江宁波·高一余姚中学校考阶段练习）在三角形中，是的中点．
（1）求在上的投影向量；
（2）若，求的取值范围．
【答案】（1）；（2）．
【解析】（1）在上的投影向量的模长即，
故在上的投影向量为．
（2），
因为，，
所以，即，，
故的取值范围为.



【变式7-3】（2022春·北京·高一北京八十中校考期末）设三角形ABC，P0是边AB上的一定点，满足P0B=AB，且对于边AB上任一点P，恒有，则三角形ABC形状为___________.
【答案】C为顶角的等腰三角形
【解析】取BC的中点D，连接PD，P0D，如图所示：

，
同理，，

，设O为AB的中点，

即三角形ABC为以C为顶角的等腰三角形.


考点8 三角形四心的判断

【例8】（2023春·陕西西安·高一长安一中校考阶段练习）已知O，N，P在的所在平面内，且，且，则O，N，P分别是的（ ）
A．重心，外心，垂心 B．重心，外心，内心
C．外心，重心，垂心 D．外心，重心，内心
【答案】C
【解析】因为，
所以到的三个顶点的距离相等，所以为的外心；
设的中点为，则由得，所以为的重心；

因为，所以，则，即，
所以，同理可得，所以为的垂心.故选：C.


【变式8-1】（2023春·高一单元测试）已知O是平面上的一个定点，A､B､C是平面上不共线的三点，动点P满足，则点P的轨迹一定经过的（ ）
A．重心 B．外心 C．内心 D．垂心
【答案】C
【解析】因为为方向上的单位向量，为方向上的单位向量，
则的方向与的角平分线一致，
由，可得，即，
所以点P的轨迹为的角平分线所在直线，
故点P的轨迹一定经过的内心.故选：C.


【变式8-2】（2023春·江苏徐州·高一校考阶段练习）（多选）已知O，N，P，I在△ABC所在的平面内，则下列说法正确的是（ ）
A．若，则O是△ABC的外心
B．若，则P是△ABC的垂心
C．若，则N是△ABC的重心
D．若，则I是△ABC的垂心
【答案】ABCD
【解析】对A，根据外心的定义，易知A正确；
对B，，同理可得：，
所以P是垂心，故B正确；
对C，记AB、BC、CA的中点为D、E、F，由题意，
则，同理可得：，则N是重心，故C正确；
对D，由题意，，则I是垂心，故D正确，故选：ABCD.


【变式8-3】（2022春·辽宁沈阳·高一校联考期中）（多选）设点是所在平面内任意一点，的内角的对边分别为，则下列结论正确的是（ ）
A．若点是的重心，则
B．若点是的垂心，则
C．若，则点是的外心
D．若，则点是的内心
【答案】ACD
【解析】对于A，若点是的重心，则，，A正确；
对于B，若点是的垂心，则，即，
，B错误；
对于C，由得：与垂直，即与垂直，
又过中点，点在的中垂线上；
同理可得：点在的中垂线上，点是的外心，C正确；
对于D，，，
即，，
；
为方向上的单位向量，为方向上的单位向量，
在的角平分线上，即为的角平分线；
同理可得：为的角平分线，点是的内心，D正确.故选：ACD.


考点9 奔驰定理解面积比
【例9】（2022春·上海宝山·高一上海交大附中校考阶段练习）设为所在平面内一点，满足，则的面积与的面积的比值为（ ）
A． B． C． D．
【答案】A
【解析】设，
因为，所以，所以O为的重心，
设，
所以，
则，
所以，所以，故选：A


【变式9-1】（2023春·安徽滁州·高一安徽省滁州中学校考阶段练习）在△ABC中，O为△ABC所在平面内的一点，且，则值为（ ）
A． B． C．3 D．
【答案】A
【解析】如图所示，分别延长到，使，
以为边作平行四边形，连接，
因为，
所以，即，
设点到的距离为，因为为中点，
由几何关系可得点到的距离为，
则点到的距离为，
所以，故选：A.


【变式9-2】（2022春·广东东莞·高一东莞市东华高级中学校考期中）已知是内部（不含边界）一点，若，，则（ ）
A． B． C． D．1
【答案】A
【解析】如图，连接AD并延长交BC与点M,
设点B到直线AD的距离为,点C到直线AD的距离为,
因为，
所以设，
因为AM与向量AD共线，
设,,

所以，即，
,
所以故选：A


【变式9-3】（2023·全国·高一专题练习）点为内一点，，则的面积之比是___________.
【答案】
【解析】因为，所以，
设为中点，为中点，为三角形的中位线，则，
因为，
可得，所以三点共线，且，
则，，
分别设，
由图可知，，，
则，所以，而，所以，
所以，，
所以，
即的面积之比等于.
故答案为：.


考点10 向量在物理中的应用

【例10】（2023春·全国·高一专题练习）图为某种礼物降落伞的示意图，其中有根绳子和伞面连接，每根绳子和水平面的法向量的夹角均为．已知礼物的质量为，降落伞自身的重量为，每根绳子的拉力大小相同．则降落伞在匀速下落的过程中每根绳子拉力的大小为（ ）（重力加速度取，精确到）．

A． B． C． D．
【答案】C
【解析】设水平面的单位法向量为，其中每一根绳子的拉力均为，如图，
，在上的投影向量为，
根绳子拉力的合力；
降落伞匀速下落，，
，解得：.故选：C.


【变式10-1】（2023春·河南·高一校联考阶段练习）（多选）若平面上的三个力作用于一点，且处于平衡状态．已知，，的夹角为，则（ ）
A． B．
C．夹角的余弦值为 D．夹角的余弦值为
【答案】BC
【解析】根据题意，画出图形：的合力为.
所以.
所以.
因为，
所以，
所以夹角的余弦值为.故选：BC


【变式10-2】（2023春·湖北武汉·高一武汉外国语学校校考阶段练习）物体在力的作用下，由点移动到点，已知，力对该物体所做功的大小为__________．
【答案】
【解析】由题意得，
所以对物体做的功．


【变式10-3】（2023春·安徽合肥·高一合肥一中校考阶段练习）有一艘在静水中速度大小为10 km/h的船，现船沿与河岸成角的方向向河的上游行驶．由于受水流的影响，结果沿垂直于河岸的方向驶达对岸．设河的两岸平行，河水流速均匀．
（1）设船相对于河岸和静水的速度分别为，河水的流速为，求之间的关系式；
（2）求这条河河水的流速．
【答案】（1）；（2）河水的流速为，方向顺着河岸向下
【解析】（1）如图，是垂直到达河对岸方向的速度，是与河岸成角的静水中的船速，
则与的夹角为，
由题意知，三条有向线段构成一个直角三角形，其中，
由向量加法的三角形法则知，，即；

（2）因为，而，
所以这条河河水的流速为，方向顺着河岸向下．



1．（2023春·云南·高一校联考阶段练习）已知力作用于一物体，使物体从点处移动到点处，则力对物体所做的功为（ ）
A．9 B． C．21 D．
【答案】C
【解析】由题意，物体从点处移动到点处，可得,
因为力，所以力对物体所做的功为.故选：C.
2．（2023春·全国·高一专题练习）已知向量，，若与的夹角是锐角，则实数的取值范围为（ ）
A． B．
C． D．
【答案】A
【解析】由题意得，，
若与的夹角是锐角，则与不共线，且它们数量积为正值，
即，且，
解得，且，
所以实数的取值范围为．故选:A
3．（2023春·重庆万州·高一重庆市万州第二高级中学校考阶段练习）在中，若，则一定是（ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．以上说法都不对
【答案】D
【解析】由，即，
又，则，即为锐角，
但不能确定B、C的大小，它们中可能存在钝角或直角或都为锐角.故选：D
4．（2023春·全国·高一专题练习）P是所在平面内一点，满足，则的形状是（ ）
A．等腰直角三角形 B．直角三角形 C．等腰三角形 D．等边三角形
【答案】B
【解析】由，可得，即，
等式两边平方，化简得，，
因此，是直角三角形.故选：B.
5．（2022春·江苏苏州·高一江苏省沙溪高级中学校考期中）在平行四边形中，分别是上的点，且，（其中），且.若线段的中点为，则当取最小值时，的值为（ ）
A．36 B．37 C．21 D．22
【答案】D
【解析】,
所以
，
所以，
因为，所以，
所以当时，取得最小值，
此时，所以.故选：D
6．（2022秋·安徽阜阳·高三校联考期中）已知，，三点共圆，，且点，，满足，若，则点到点的距离的最大值为（ ）
A． B． C． D．
【答案】D
【解析】作出图形如图所示，取线段的中点．
因为，
所以，故
，故点在以为圆心，为半径的圆上，
则点到点的距离．
设，，所在圆的圆心为，
则当，，三点共线，即点在线段上，
时，取到最大值，
此时为等边三角形，故，
则点到点的距离的最大值为．故选：D.
7．（2022春·山东泰安·高一泰安一中校考期中）如图，AB为半圆的直径，点C为的中点，点M为线段AB上的一点（含端点A，B），若，则的取值范围是（ ）

A． B． C． D．
【答案】D
【解析】因为点C为的中点，，所以，
所以
，
因为点M为线段AB上的一点，所以，所以，
所以的取值范围是,故选：D.
8．（2022春·广东佛山·高一校考期中）已知，且关于的方程有实根，则与的夹角的取值范围是
A． B． C． D．
【答案】B
【解析】关于的方程有实根
设与的夹角为，则
又
又 本题正确选项：
9．（2022春·广东江门·高一江门市培英高级中学校考期中）已知在中，点在线段的延长线上，若，点在线段上，若，则实数的取值范围（ ）
A． B． C． D．
【答案】A
【解析】如图设，

，则，
则

故选：
10．（2022春·湖南邵阳·高一统考期中）在中，点满足，过点的直线与，所在的直线分别交于点，，若，，则的最小值为（ ）
A．3 B． C．1 D．
【答案】A
【解析】由题设，如下图示：，
又，，

∴，由三点共线，有，
∴，
当且仅当时等号成立.故选：A
11．（2023春·安徽马鞍山·高一马鞍山二中校考阶段练习）（多选）关于船从两平行河岸的一岸驶向另一岸所用的时间，正确的是（ ）
A．船垂直到达对岸所用时间最少
B．当船速的方向与河岸垂直时用时最少
C．沿任意直线航行到达对岸的时间都一样
D．船垂直到达对岸时航行的距离最短
【答案】BD
【解析】设船在静水中的速度为，水流速度为，船实际速度为，两岸间的垂直距离为；
对于ABC，船垂直到达对岸时，，则所用时间；
当船速的方向与河岸垂直时，所用时间；
，当船速的方向与河岸垂直时，用时最少，
且沿不同直线航行到达对岸的事件不相同，A错误，B正确，C错误；
对于D，船垂直到达对岸时，航行的距离为两岸间的垂直距离，此时距离最短，D正确.
故选：BD.
12．（2023·全国·高一专题练习）（多选）点在所在的平面内，（ ）
A．若动点满足，则动点的轨迹一定经过的垂心
B．若动点满足，则动点的轨迹一定经过的重心
C．若，，分别表示，的面积，则
D．已知三个内角，，的对边分别是，，，若，则点为的内心（内切圆圆心）
【答案】CD
【解析】对于A，设的中点为，连，如图：
因为，所以，
所以，即与共线，
所以动点的轨迹一定经过的重心，故A不正确；
对于B，由A可知，只有当时，
动点的轨迹才经过的重心，故B不正确；
对于C，因为，所以，
设、的中点分别为、，则，
所以，故C正确；
对于D，延长交于，
因为，所以，
所以，
设，，则，
因为与不共线，所以，，
所以，即，所以，即，
所以为的平分线，同理得为的平分线，为的平分线，
所以为的内心.故D正确.故选：CD
13．（2023春·安徽淮北·高一淮北师范大学附属实验中学校考阶段练习）（多选）生于瑞士的数学巨星欧拉在1765年发表的《三角形的几何学》一书中有这样一个定理：“三角形的外心、垂心和重心都在同一直线上．”这就是著名的欧拉线定理．在中，O，H，G分别是外心、垂心和重心，D为BC边的中点，下列四个选项中正确的是（ ）
A． B． C． D．
【答案】ABCD
【解析】在中，O，H，G分别是外心、垂心和重心，画出图形，如图所示．

对于B选项，根据三角形的重心性质由重心的性质可得为的三等分点，且，
又为的中点，所以，所以，故选项B正确；
对于A与C选项，因为O为的外心，为的中点，
所以，所以，∴，
∴，∴，，故选项A，C正确；
对于D，过点G作，垂足为E，∴，则，
∴的面积为；
同理，，选项D正确.故选：ABCD
14．（2023春·湖南常德·高一临澧县第一中学校考阶段练习）（多选）如图.为内任意一点，角的对边分别为，总有优美等式成立，因该图形酯似奔驰汽车车标，故又称为奔驰定理.则以下命题是真命题的有（ ）

A．若是的重心，则有
B．若成立，则是的内心
C．若，则
D．若是的外心，，，则
【答案】AB
【解析】对于A：如图所示：因为分别为的中点，
所以，，
同理可得、，所以，
又因为，所以.正确；

对于B：记点到的距离分别为，
，
因为，则，
即，
又因为，所以，所以点是的内心，正确；
对于C：因为，所以，所以，
所以，
所以，
化简得：，
又因为不共线，所以，所以，
所以，错误；
对于D：因为是的外心，，所以,，
所以，
因为，则，
化简得：，由题意知同时为负，
记，，则，
因为，所以，所以，
所以，错误.故答案为：AB.
15．（2023春·湖北武汉·高一湖北省武昌实验中学校考阶段练习）如图，在菱形ABCD中，，，若菱形的边长为6，则的取值范围为__________．

【答案】
【解析】依题意，因为在菱形ABCD中，，，
所以，
所以
，
因为，所以.
16．（2023春·全国·高一专题练习）半径为2的圆上有三点，，，满足，点是圆内一点，则的取值范围是________．
【答案】
【解析】由得，
所以四边形是平行四边形，
又，则四边形是菱形，
易得是等边三角形，
所以，
设四边形对角线的交点为E，，
由极化恒等式得，
，
所以，
因为是圆内一点，所以，所以，即.
17．（2023春·河南开封·高一校考阶段练习）已知等腰直角三角形的斜边，为三角形所在平面内任意一点，则的最小值为_________.
【答案】
【解析】以所在直线为轴，以边上的高所在直线为轴，
建立如图所示直角坐标系：

为等腰直角三角形，，所以易得，
故,，设，
则，，
则，
，
当，时，的最小值为，
18．（2023春·江苏南通·高一南通一中校考阶段练习）设点是面积为4的内部一点，且有，则的面积为__________.
【答案】
【解析】
；
设；则：,即B,C,D三点共线；
所以；；
19．（2023春·河北保定·高一保定一中校考阶段练习）如图，在平行四边形中，点是的中点，是的三等分点. ，设.

（1）用表示；
（2）如果，用向量的方法证明：.
【答案】（1），；（2）证明见解析
【解析】（1）由题意，，
；
（2）由（1）得，
所以.
20．（2023秋·辽宁·高一校联考期末）已知m>0，n>0，如图，在中，点M，N满足，，D是线段BC上一点，，点E为AD的中点，且M，N，E三点共线．

（1）若点O满足，证明：．
（2）求的最小值．
【答案】（1）证明见解析；（2）
【解析】（1）由题可知，
因为点E为AD的中点，所以．
由，则，即，
，
又所以，又三点不共线，所以．
（2）因为M，N，E三点共线，
所以可设，又，，
所以
又， 所以，所以，
所以，
当且仅当，时，等号成立．所以的最小值是．