初中数学人教版九年级上册24.1.2 垂直于弦的直径精品课件ppt

这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径精品课件ppt，共25页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，圆有哪些对称轴，垂径定理，推导格式等内容，欢迎下载使用。

1. 进一步认识圆，了解圆是轴对称图形.2.理解垂直于弦的直径的性质和推论，并能应用它解决一些简单的计算、证明和作图问题. （重点）3.灵活运用垂径定理解决有关圆的问题. （难点）
连接圆上任意两点的线段叫做弦.
(2)圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合．
(1)在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点所形成的图形叫做圆．
圆上任意两点间的部分叫做弧.
你能通过折叠的方式找到圆形纸片的对称轴吗？在折的过程中你有何发现？什么是轴对称图形？我们学过哪些轴对称图形？
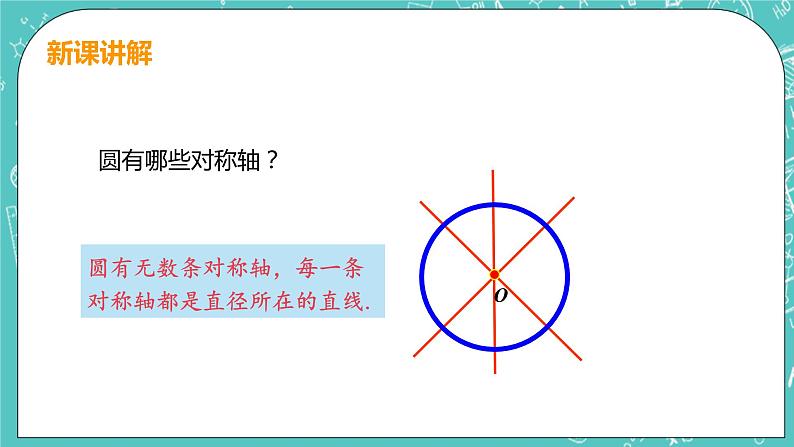
知识点1 圆的对称性
　 用纸剪一个圆，沿着圆的任意一条直径所在的直线对折，重复做几次，你发现了什么？由此你能得到什么结论？
发现：圆是轴对称图形，任何一条直径所在直线都是它的对称轴．　
圆有无数条对称轴，每一条对称轴都是直径所在的直线.
1 求证：圆是轴对称图形，任何一条直径所在的直线都是圆的对称轴.
导引：要证明圆是轴对称图形，只需证明圆上任意一点关于直径所在直线(对称轴)的对称点也在圆上.
证明：如图，设CD是⊙O的任意一条直径，A为⊙O上点C,D以外的任意 一点.过点A作AA′⊥CD，交⊙O于点A′，垂足为M，连接OA，OA′. 在△OAA′中，∵OA=OA′, ∴△OAA′是等腰三角形. 又AA′⊥CD，∴AM=MA′. 即CD是AA′的垂直平分线. 这就是说，对于圆上任意一点A， 在圆上都有关于直线CD的对称点A′，因此⊙O关于直线CD对称. 即圆是轴对称图形，任何一条直径所在直线都是圆的对称轴.
知识点2 垂径定理
2 如图，AB是⊙O的一条弦，直径CD⊥AB，垂足为E.你能发现图中有哪些相等的线段和劣弧? 为什么?
答：线段: AE=BE
垂直于弦的直径平分弦，并且平分弦所对的两条弧.
垂径定理的几个基本图形：
如果把垂径定理（垂直于弦的直径平分弦，并且平分弦所对的两条弧）结论与题设交换一条，命题是真命题吗？
①过圆心 ；②垂直于弦；③平分弦（非直径）；④平分弦所对的优弧 ； ⑤平分弦所对的劣弧.在一个圆中，一条直线只要满足上面五个条件中的任意两个，都可以推出其他三个结论(知二推三).
“不是直径”这个条件能去掉吗？如果不能，请举出反例.
平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧.
3 赵州桥（如图）是我国隋代建造的石拱桥，距今约有1 400年的历史，是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形，它的跨度（弧所对的弦的长）为37 m，拱高（弧的中点到弦的距离）为7.23 m，求赵州桥主桥拱的半径（结果保留小数点后一位）.
分析：解决此问题的关键是根据赵州桥的实物图画出几何图形.
在Rt△OAD中，由勾股定理，得OA2=AD2+OD2，即R2=18.52+（R-7.23）2. 解得R≈27.3.因此，赵州桥的主桥拱半径约为27.3 m.
由题设可知AB=37，CD=7.23，
在圆中有关弦长a，半径r，弦心距d（圆心到弦的距离），弓形高h的计算题时，常常通过连半径或作弦心距构造直角三角形，利用垂径定理和勾股定理求解.
涉及垂径定理时辅助线的添加方法
弦a，弦心距d，弓形高h，半径r之间有以下关系：
d+h=r
如图，AB是圆O的弦，半径OC⊥AB于点D，若圆O的半径为5，AB=8，则CD的长是( )
A.2B.3C.4D.5
一条直线满足:①过圆心;②垂直于弦; ③平分弦（不是直径）; ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其他三个结论（“知二推三”）
垂直于弦的直径平分弦，并且平分弦所对的两条弧
两条辅助线：连半径，作弦心距
构造直角三角形，利用勾股定理计算或建立方程.
1.如图，⊙O的弦AB垂直于半径OC，垂足为D，则下列结论中错误的是( )A.∠AOD=∠BOD B.AD=BD C.OD=DC D.AC=BC2.半径为5的⊙O内有一点P，且OP=4，则过点P的最长弦的长是 ，最短弦的长是 .
3.如图，一条公路的转弯处是一段圆弧AB，点O是这段弧的圆心，AB＝300m，C是AB上一点，OC⊥AB，垂足为D，CD＝45m，求这段弯路的半径.解：设半径为r.∵OC⊥AB，∴AD=BD= AB=150m.在Rt△ODB中，OD2+BD2=OB2，即(r-45)2+1502=r2, 解得r=272.5m.因此，这段弯路的半径为272.5m.
4.如图，两个圆都以点O为圆心.求证：AC=BD.证明：过O作OE⊥AB，垂足为E，连接OA,OC,OD,OB,则AE=BE，CE=DE，∴AE-CE=BE-DE，即AC=BD.
如图，AB和CD分别是⊙O上的两条弦，圆心O到它们的垂线段分别是OM和ON，如果AB＞CD，OM和ON的大小有什么关系？为什么？