数学九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆公开课课件ppt

这是一份数学九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆公开课课件ppt，共25页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，弦的概念，弧的概念，∠AOB为圆心角等内容，欢迎下载使用。

1.理解圆心角的概念，掌握圆的中心对称性和旋转不变性. 2.探索圆心角、弧、弦之间关系定理并利用其解决相关问题. （重点） 3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义. （难点）
连接圆上任意两点的线段叫做弦.
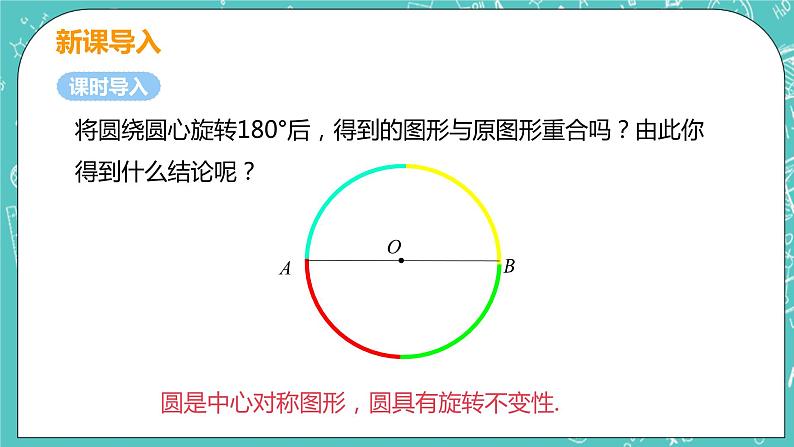
圆是中心对称图形，圆具有旋转不变性.
将圆绕圆心旋转180°后，得到的图形与原图形重合吗？由此你得到什么结论呢？
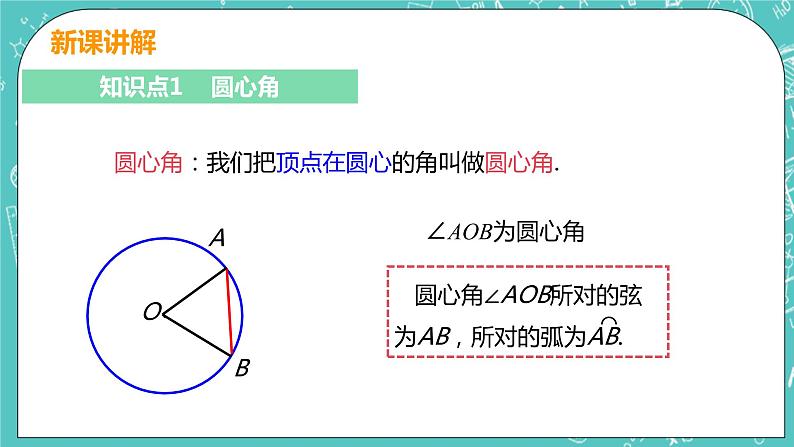
知识点1 圆心角
圆心角：我们把顶点在圆心的角叫做圆心角.
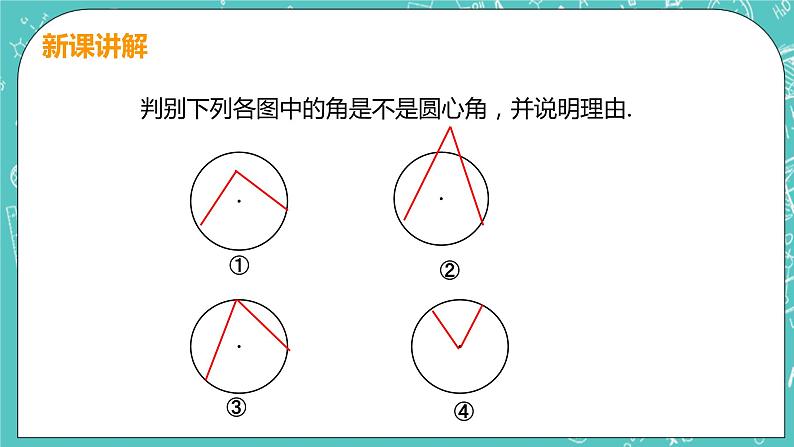
判别下列各图中的角是不是圆心角，并说明理由.
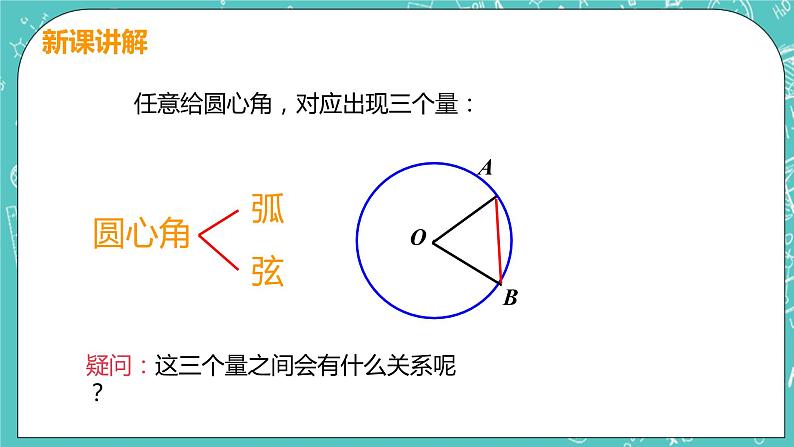
任意给圆心角，对应出现三个量：
疑问：这三个量之间会有什么关系呢？
1.下面四个图形中的角，是圆心角的是(　　)
2. 如图，AB为⊙O的弦，∠A＝40°，则AB所对的圆 心角等于(　　) A．40° B．80° C．100° D．120°
知识点2 圆心角与所对的弧、弦之间的关系
1 如图，将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置，你能发现哪些等量关系？为什么？
∵ ∠AOB=∠A1OB1
如图，⊙O与⊙O1是等圆，∠AOB =∠A1OB1=60°，请问上述结论还成立吗？为什么?
在同一个圆中，如果圆心角相等，那么它们所对的弧相等，所对的弦相等．
弧、弦与圆心角的关系定理
定理“在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等”中，可否把条件“在同圆或等圆中”去掉？为什么？
在同一个圆中，如果弧相等，那么它们所对的圆心角相等，所对的弦相等．
弧、弦与圆心角关系定理的推论
在同一个圆中，如果弦相等，那么它们所对的圆心角相等，所对的弧相等．
∴ AB=AC．△ABC是等腰三角形.
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB＝∠BOC＝∠AOC.
2 如图，在⊙O中， AB=AC ，∠ACB=60°，求证∠AOB=∠BOC=∠AOC.
弦、弧、圆心角的关系定理
①要注意前提条件；②要灵活转化.
1.如图，AB是⊙O的直径，BC=CD=DE,∠AOE=72°，则∠COD的度数是( )A．36° B．72° C．108° D．48°2.如图，已知AB是⊙O的直径，C、D是半圆上两个三等分点，则∠COD= .
3.如图，在⊙O中，AB=AC，∠C=75°，求∠A的度数.解：∵AB=AC，∴AB=AC.∴∠B=∠C=75°，∴∠A=180°-∠B -∠C=30°.
4.如图，在⊙O中，AD=BC，求证：AB=CD.证明：∵AD=BC.∴AD=BC.∴AD+AC=BC+AC,即CD=AB.∴AB=CD.
如图，在⊙O中，弦AB与CD相交于点E，AB=CD．(1)求证：△AEC≌△DEB；(2)点B与点C关于直线OE对称吗？试说明理由．
(1)证明：连接AD.∵AB=CD, ∴AB=CD. ∴AB-AD=CD-AD.即BD=AC. ∴BD=AC.在△ADB和△DAC中，∴△ADB≌△DAC(SSS).
∴∠ABD＝∠DCA.在△AEC和△DEB中，∠DCA＝∠ABD,∠AEC＝∠DEB,AC=BD,∴△AEC≌△DEB(AAS).