九年级上册24.1.4 圆周角优质课件ppt

这是一份九年级上册24.1.4 圆周角优质课件ppt，共28页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，OAOC，∠A∠C，解∠1∠2等内容，欢迎下载使用。

1.理解圆周角的概念，会叙述并证明圆周角定理. 2.理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题. （重难点） 3.理解掌握圆周角定理的推论及其证明过程和运用. （难点）
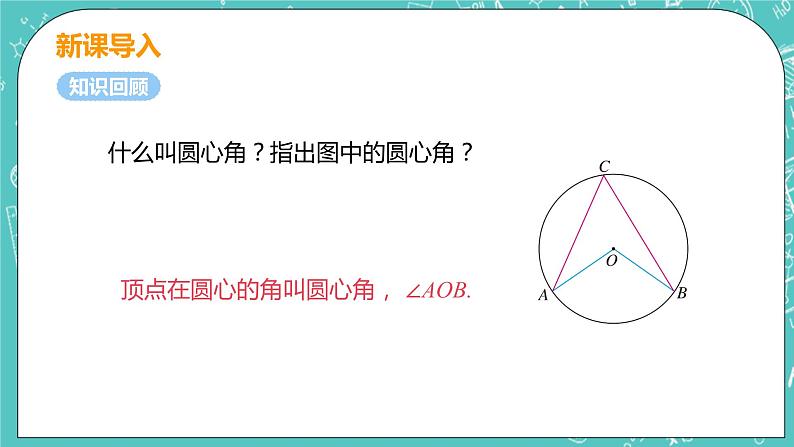
什么叫圆心角？指出图中的圆心角？
顶点在圆心的角叫圆心角， ∠AOB.
如图，∠ACB的顶点和边有哪些特点?
∠ACB的顶点在☉O上，角的两边分别交☉O于B，A两点.
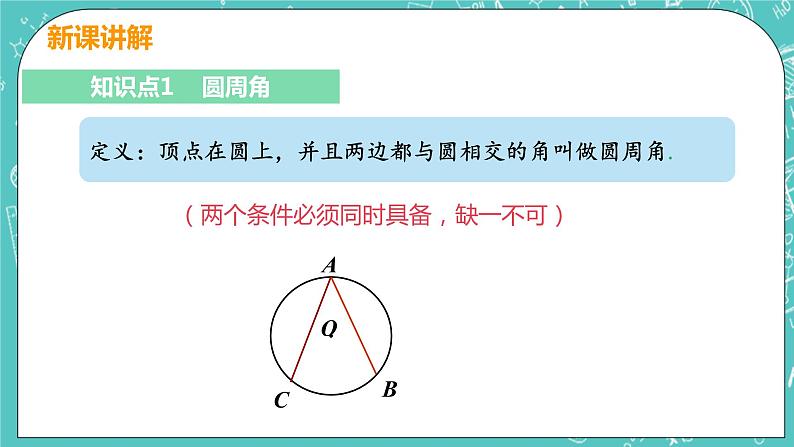
知识点1 圆周角
定义：顶点在圆上，并且两边都与圆相交的角叫做圆周角.
（两个条件必须同时具备，缺一不可）
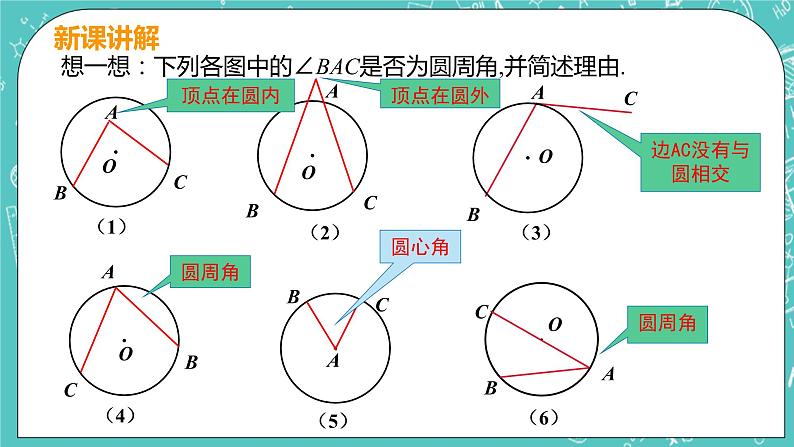
想一想：下列各图中的∠BAC是否为圆周角,并简述理由.
知识点2 圆周角定理及其推论
想一想：1.图中圆心角∠BOC与圆周角∠BAC存在怎样的数量关系.
2.是不是所有的圆心角和圆周角都符合这个数量关系呢？需要满足什么样的条件呢？
（1）当圆心O在∠BAC的一边上时（特殊情形）
∠BOC= ∠ A+ ∠C
（2）圆心O在∠BAC的内部时
（3）当圆心O在∠BAC的外部时
圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.
推论1 同弧或等弧所对的圆周角相等.
想一想：怎样证明等弧所对的圆周角相等呢？通过一道题目来探讨一下.
如图，点A、B、C、D在同一个圆上，AC、BD为四边形ABCD的对角线.
推论2半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径.
想一想：如图，点A，B，C，D在同一个圆上，AC，BD为四边形ABCD的对角线.
若AC是半圆，∠ADC = ，∠ABC = .
1 如图，⊙O的直径AC为10cm，弦AD为6cm.（1）求DC的长；
（2）若∠ADC的平分线交⊙O于B, 求AB、BC的长．
在Rt△ABC中，AB2+BC2=AC2，
(2)∵ AC是直径,∴ ∠ABC=90°. ∵BD平分∠ADC,∴∠ADB=∠CDB. 又∵∠ACB=∠ADB ,∠BAC=∠BDC . ∴ ∠BAC=∠ACB, ∴AB=BC.
知识点3 圆内接四边形及其性质
如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.
2 如图，四边形ABCD为⊙O的内接四边形，⊙O为四边形ABCD的外接圆.
猜想：∠A与∠C, ∠B与∠D之间的关为 .
∠A+ ∠C=180º，∠B+ ∠D=180º
圆内接四边形的性质：圆内接四边形的对角互补.
∵∠A＋∠DCB＝180°，
∠DCB＋∠DCE＝180°.
3 如图，∠DCE是圆内接四边形ABCD的一个外角，∠A与∠DCE的大小有何关系？
4 如图，AB为⊙O的直径，CF⊥AB于E，交⊙O于D，AF交⊙O于G. 求证：∠FGD＝∠ADC.
证明：∵四边形ACDG内接于⊙O，∴∠FGD＝∠ACD.又∵AB为⊙O的直径，CF⊥AB于E，∴AB垂直平分CD，∴AC＝AD，∴∠ADC＝∠ACD，∴∠FGD＝∠ADC.
在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等.
90°的圆周角所对的弦是直径.
1.顶点在圆上，2.两边都与圆相交的角（二者必须同时具备）.
半圆或直径所对的圆周角都相等，都等于90°（直角）
圆内接四边形的角的“三种关系”：
1.对角互补，若四边形ABCD为⊙O的内接四边形，则∠A＋∠C＝180°，∠B＋∠D＝180°.2.四个内角的和是360°，若四边形ABCD为⊙O 的内接四边形，则∠A＋∠B＋∠C＋∠D＝360°.3.任一外角与其相邻的内角的对角相等，简称圆内接四边形的外角等于其内对角．
1.下列四个图中，∠x是圆周角的是( )
2.如图，⊙O中，弦AD平行于弦BC，∠AOC=78°，求∠DAB的度数．解：∵AD∥BC， ∴∠DAB=∠B. 又∵∠B= ∠AOC=39°. ∴∠DAB=39°.
3.如图，⊙O的半径为1，A,B,C是⊙O上的三个点，且∠ACB=45°，求弦AB的长.解：连接OA、OB.∵∠ACB=45°,∴∠BOA=2∠ACB=90°.又OA=OB, ∴△AOB是等腰直角三角形.
4.如图，已知EF是⊙O的直径，把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上，斜边AB与⊙O交于点P，点B与点O重合；将三角形ABC沿OE方向平移，使得点B与点E重合为止．设∠POF=x°，则x的取值范围是 ．
如图，BC为半圆O的直径，点F是BC上一动点(点F不与B、C重合)，A是BF上的中点，设∠FBC=α，∠ACB=β．(1)当α=50°时，求β的度数;(2)猜想α与β之间的关系，并给予证明.