





- 九年级数学人教版上册 第24章 圆 24.1 圆的有关性质 24.1.3 弧、弦、圆心角 课件 课件 10 次下载
- 九年级数学人教版上册 第24章 圆 24.1 圆的有关性质 24.1.4 圆周角 课件 课件 10 次下载
- 九年级数学人教版上册 第24章 圆 24.2 点和圆、直线和圆位置关系 24.2.2课时1 直线和圆的位置关系 课件 课件 9 次下载
- 九年级数学人教版上册 第24章 圆 24.2 点和圆、直线和圆位置关系 24.2.2课时2 切线的判定和性质 课件 课件 9 次下载
- 九年级数学人教版上册 第24章 圆 24.2 点和圆、直线和圆位置关系 24.2.2课时3 切线长定理及三角形的内切圆 课件 课件 9 次下载
初中数学人教版九年级上册24.2.1 点和圆的位置关系精品ppt课件
展开1.理解并掌握点和圆的三种位置关系. (难点)2.理解不在同一直线上的三个点确定一个圆及其运用. (重点) 3.了解三角形的外接圆和三角形外心的概念.4.了解反证法的证明思想.
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
问题: 观察下列图片.是一个小朋友玩飞镖游戏时在靶子上留下的小孔,这些小孔和这些同心圆是什么关系呢?
知识点1 点和圆的位置关系
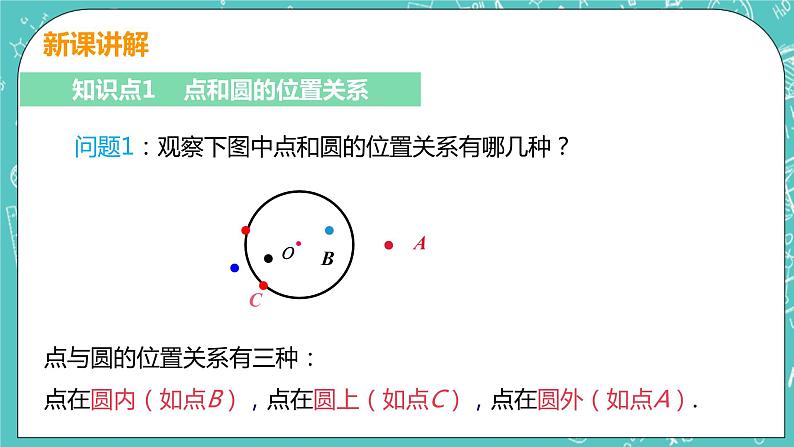
问题1:观察下图中点和圆的位置关系有哪几种?
点与圆的位置关系有三种:点在圆内(如点B),点在圆上(如点C),点在圆外(如点A).
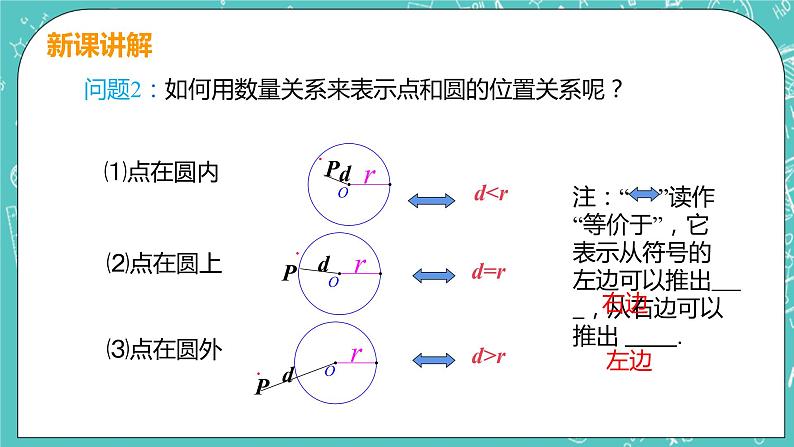
问题2:如何用数量关系来表示点和圆的位置关系呢?
注:“ ”读作“等价于”,它表示从符号的左边可以推出 ,从右边可以推出 .
1 画出由所有到已知点O的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
∴阴影部分就是所求图形.
(湘西州)⊙O的半径为5 cm,点A到圆心O的距 离OA=3 cm,则点A与圆O的位置关系为( ) A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
知识点2 确定圆的条件
如何过一个点A作一个圆?过点A可以作多少个圆?
答:任取一点为圆心,以圆心到点A的距离为半径,画圆,可作无数个圆.
如何过两点A、B作一个圆?过两点可以作多少个圆?
分析:作线段AB的垂直平分线,以其上任意一点为圆心,以这点到点A或点B的距离为半径画圆即.
过不在同一直线上的三点能不能确定一个圆?
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
不在同一直线上的三个点确定一个圆.
活学巧记过一点可作无数圆;过两点可作圆无数,圆心全在一直线;过三点能作一个圆,前提是三点不共线.
如图,点A,B,C在同一条直线上,点D在直线AB外,过这4个点中的任意3个点画圆,能画圆的个数是( )
A.1B.2C.3D.4
知识点3 三角形的外接圆
已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
1. 外接圆与内接三角形⊙O叫做△ABC的外接圆, △ABC叫做⊙O的内接三角形.
到三角形三个顶点的距离相等.
三角形外接圆的圆心叫做三角形的外心.
三角形三边垂直平分线的交点.
一个圆可以有无数个内接三角形,但是一个三角形只有一个外接圆.
1.作三角形任意两边的垂直平分线,确定其交点;2.以该交点为圆心,交点到三个顶点中任意一点的距离为半径作圆即可.
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内;直角三角形的外心位于直角三角形斜边的中点;钝角三角形的外心位于三角形外.
如图, ⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4.求AC的长.
知识点4 反证法
经过同一条直线上的三个点能作出一个圆吗?
如图,假设过同一条直线l上三点A,B,C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l 这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
先假设命题的结论不成立,然后经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
假设命题的结论不成立,从这个假设出发,经过推理,得出矛盾,由矛盾判定假设不正确,从而肯定原命题的结论正确.
①命题的结论的表述为“肯定”或“否定”,且用直接法证较困难;②证明一个定理的逆命题,用直接法证较困难.使用反证法的前提条件是“结论”的反面可列举出来.
如图,我们要证明:如果AB∥CD,那么∠1=∠2.假设∠1≠∠2,过点O作直线A′B′,使∠EOB′=∠2.根据“同位角相等,两直线平行”,可得A′B′∥CD.这样,过点O就有两条直线AB,A′B′都平行于CD,这与平行公理“过直线外一点有且仅有一条直线与已知直线平行”矛盾.这说明假设∠1≠∠2不正确,从而∠1=∠2.
用反证法证明平行线的性质“两直线平行,同位角相等”.
定理:过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的
反证法的证明思想:反设、归谬、结论
1.判断下列说法是否正确:(1) 任意的一个三角形一定有一个外接圆.( )(2) 任意一个圆有且只有一个内接三角形.( )(3) 经过三点一定可以确定一个圆.( )(4) 三角形的外心到三角形各顶点的距离相等.( )
2.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 . 3.若一个三角形的外心在一边上,则此三角形的形状为( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
4.爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,已知这个导火索的长度为18cm,点导火索的人以每秒6.5m的速度撤离是否安全?为什么?解:由题意可知,导火索燃烧完需18÷0.9=20(S).又点导火索的人以每秒6.5m的速度撤离,则导火索燃烧完时撤离的最大距离为6.5×20=130(m).∵130>120,∴安全.
初中数学人教版九年级上册24.2.1 点和圆的位置关系图片ppt课件: 这是一份初中数学人教版九年级上册24.2.1 点和圆的位置关系图片ppt课件,共24页。PPT课件主要包含了点和圆的位置关系,点在圆内,d﹤r,点在圆上,点在圆外,d=r,练一练,﹤r﹤5,不能作出,为什么等内容,欢迎下载使用。
数学九年级上册24.2.1 点和圆的位置关系教学课件ppt: 这是一份数学九年级上册24.2.1 点和圆的位置关系教学课件ppt,共23页。PPT课件主要包含了学习目标,情景引入,知识精讲,针对练习,数形结合,位置关系,数量关系,典例解析,达标检测,小结梳理等内容,欢迎下载使用。
初中数学人教版九年级上册24.2.1 点和圆的位置关系教课课件ppt: 这是一份初中数学人教版九年级上册24.2.1 点和圆的位置关系教课课件ppt,共25页。PPT课件主要包含了课堂练习等内容,欢迎下载使用。













