【新题速递】人教版数学6年级下册第3期02

这是一份【新题速递】人教版数学6年级下册第3期02，共17页。

【新题速递】人教版数学6年级下册
第3期 02
一、选择题
1．（2023秋·北京延庆·六年级统考期末）关于圆的认识，下面说法中（ ）的观点是不正确的。
A．井盖是圆形，因为井盖边缘到圆心距离相等，井盖不会掉入井中
B．圆规两脚间的距离长，画出的圆就大
C．圆的半径扩大到原来的3倍，这个圆的面积就扩大到原来的9倍
D．圆半径的长度是直径的
2．（2023秋·北京昌平·六年级统考期末）卡塔尔世界杯于2022年11月21日至12月18日举行，这是世界杯首次在中东国家境内举行。卡塔尔世界杯的主体育场名为“卢赛尔体育场”，可以同时容纳4万人，远观整个体育场像是沙漠中的一只金碗。特别需要注意的是，这座美丽的“沙漠金碗”是由中国铁建国际集团承建的。许多体育场都会把观众席设计成围绕球场一周的圆形，这样的设计应用的是圆形特征中的（ ）。
A．圆心决定圆的位置B．半径决定圆的大小
C．同圆中直径是半径的2倍D．同圆中的半径都相等
3．（2023秋·北京昌平·六年级统考期末）冬季比较寒冷，城市绿化部门的工作人员一般会给树木“穿冬衣”。方法是用粗麻绳围绕树木转几圈，直到把树木外围都绕上麻绳。一位工作人员在给一棵树木穿“衣服”时发现用了25.12米长的麻绳，她立刻数了数一共捆了16周，然后马上就估算出了树干横截面的直径。下列（ ）算式可以表示工作人员的想法。
A．25.12÷16B．25.12÷3.14
C．25.12÷16÷3.14D．25.12÷16÷3.14÷2
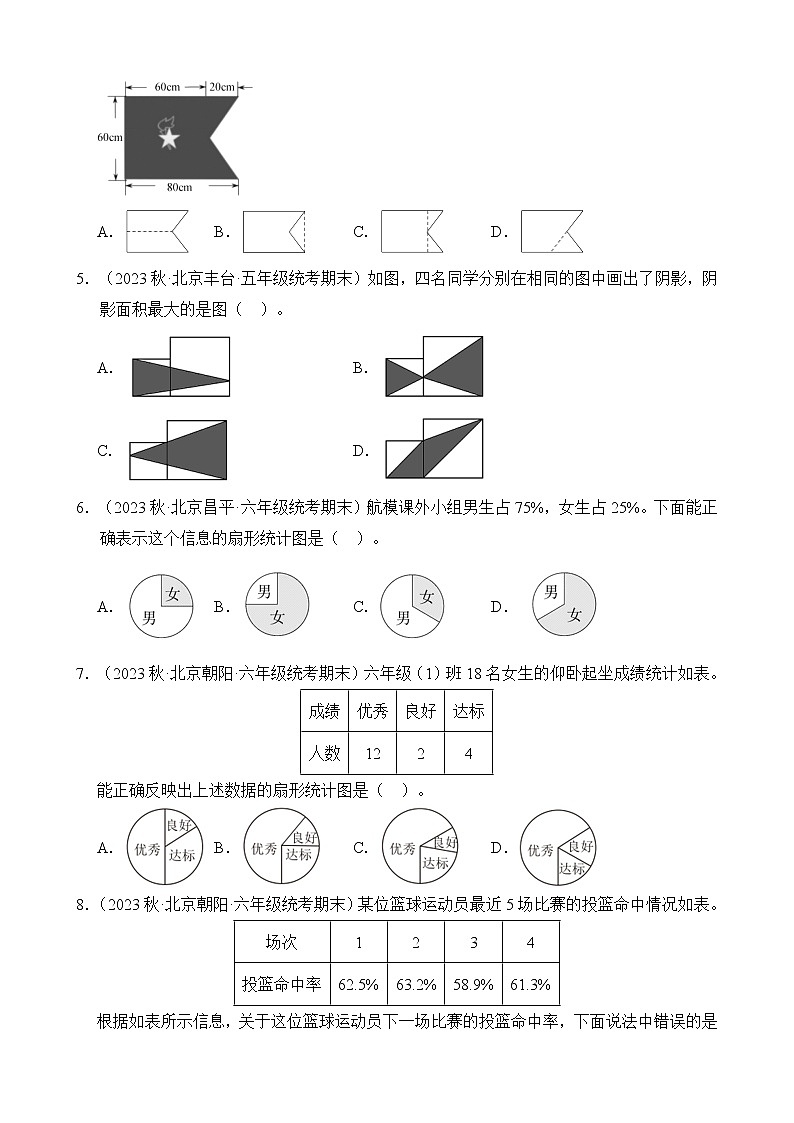
4．（2023秋·北京丰台·五年级统考期末）如图是少先队中队旗。下面四个选项是计算中队旗面积的不同方法。图（ ）的方法与算式“”相对应。
A．B．C．D．
5．（2023秋·北京丰台·五年级统考期末）如图，四名同学分别在相同的图中画出了阴影，阴影面积最大的是图（ ）。
A．B．
C．D．
6．（2023秋·北京昌平·六年级统考期末）航模课外小组男生占75%，女生占25%。下面能正确表示这个信息的扇形统计图是（ ）。
A．B．C．D．
7．（2023秋·北京朝阳·六年级统考期末）六年级（1）班18名女生的仰卧起坐成绩统计如表。
能正确反映出上述数据的扇形统计图是（ ）。
A．B．C．D．
8．（2023秋·北京朝阳·六年级统考期末）某位篮球运动员最近5场比赛的投篮命中情况如表。
根据如表所示信息，关于这位篮球运动员下一场比赛的投篮命中率，下面说法中错误的是（ ）。
A．投篮命中率可能在60%左右B．投篮命中率可能低于60%
C．投篮命中率可能达到70%D．投篮命中率一定大于50%
二、填空题
9．（2022秋·北京丰台·六年级统考期末）如图，直径2分米的圆贴着直角三角形的边在外侧滚动一周，回到起点时，圆心经过的路线长( )分米。
10．（2022春·四年级单元测试）垂线画法知多少。
过直线外一点画垂线的方法：①把三角尺的一条( )与已知直线( )；②沿着直线移动三角尺( )位置；③沿着三角尺的( )画一条直线；④标出( )。
11．（2023秋·北京·五年级统考期末）看图填空。
(1)图中平行四边形ABCD各个顶点的位置如图，如果A点用数对表示是（1，2），那么其余各顶点的位置是：B点的位置是______；C点的位置是______；D点的位置是______；
(2)如果图中平行四边形向上平移3格，那么平移后A点的位置是______。
12．（2022秋·北京丰台·六年级统考期末）一年级小朋友两臂伸平后长度约是1.2米，30个小朋友手拉手围成一个圆圈做投掷游戏，靶子放在围成的圆圈中心位置，每个小朋友距离靶子大约是( )米。（得数保留整数）
13．（2023秋·北京丰台·五年级统考期末）在全世界红树林面积每年递减的背景下，位于我国大陆最南端的广东湛江红树林国家级自然保护区的红树林面积却逐年增长，保护区总面积为202.788平方千米，合________公顷，被国际湿地专家称为世界湿地恢复地成功典范。
14．（2023秋·北京朝阳·六年级统考期末）在停车场的出入口都有起落杆。这根起落杆完成一次升起运动（如图），起落杆最远端（A点）移动了( )m。
15．（2022·北京海淀·校考小升初真题）甲、乙两公司组织员工进行登山友谊赛，甲公司有86人参加，乙公司有80人参加，两公司员工登山情况如下图所示：
(1)在登到( )米高度时，两公司员工登山的人数是一样的。
(2)甲公司登山人数在( )米至( )米之间时，人数减少的最快。
(3)乙公司员工登到1000米时，还剩下( )%的人仍然在坚持登山。
16．（2022·北京海淀·校考小升初真题）“龟兔赛跑”的故事大家都熟悉，如图是兔子比赛时的情况。从图中可以判断出兔子睡醒后的速度比睡觉前的速度( )。（填“快”或“慢”）
17．（2022·北京海淀·统考小升初真题）摩天轮转动过程中，笑笑所在座舱高度的变化情况可以用下图来表示。
(1)在摩天轮转动过程中，笑笑所在座舱的高度随着( )的变化而变化，笑笑坐摩天轮转动一圈需要( )分。
(2)转动第一圈的过程中，从( )分到( )分高度在增加，从( )分到( )分高度在降低。
三、作图题
18．（2023秋·北京·六年级统考期末）如图，小聪在方格纸中画了图案的一部分，整个图案是由2个这样的图组成，且没有重叠，请你用直尺和圆规在方格纸上将整个图补充完整并涂出阴影部分。
四、解答题
19．（2022春·四年级单元测试）如果两条平行线被一条直线所截（如图），会产生很多个有联系的角。
（1）请用量角器测量∠1、∠2，你发现了什么？
（2）根据上面得到的结论，观察∠3、∠5，通过推理说明∠3和∠5的关系。
20．（2023秋·北京朝阳·五年级统考期末）同学们在研究如何解决平行四边形面积的问题时，想到了以下的方法：
①在你认为可以推导出平行四边形面积公式的同学名字下画“√”。
②这学期我们在研究其他平面图形面积的过程中也使用过这样的思路。请你选择其中一种平面图形，表达出它的推导过程。
21．（2023秋·北京大兴·五年级统考期末）我国古代数学名著《九章算术》中的“方田章”记载着这样一种求长方形面积的方法：广从相乘得积步。“广”和“从”是指长和宽。还记载着一种求三角形面积的方法：半广以乘正从。你能结合下图解释“方田章”中求三角形面积方法的道理吗？
22．（2023秋·北京朝阳·五年级统考期末）要画一个等腰梯形，已经确定了3个顶点（如下图），最后一个顶点所在的位置用数对表示可能为（ ）。请在下图中画出这个等腰梯形。
23．（2023秋·北京密云·五年级统考期末）如下图，平行四边形被分成①号三角形和②号三角形，这两个三角形的面积都是270平方米。
（1）请根据以上信息提出一个数学问题并解答。
我提出的问题是：
解答：
（2）下面是乐乐同学的解答方法：
分析乐乐的解答方法，他的方法解决了哪个数学问题？请写下来。
24．（2023秋·北京昌平·五年级统考期末）为了更好的开展劳动教育，丰富同学们的种植体验，学校整理出一块长16米，宽10米的种植实践基地。为了方便同学们种植，学校在实践基地的中央修了一条小路（如图，阴影为可种植部分），你能帮忙算一算可种植部分的面积是多少平方米吗？
25．（2023秋·北京西城·五年级统考期末）将一张长方形纸剪一刀，剪成了一个三角形和一个梯形。（单位：厘米）
（1）这张长方形纸的面积是多少平方厘米？
（2）如果在梯形中继续剪，最多还可以剪出多少个图中的三角形？（注：三角形不能拼接）下面是小红的想法。
你同意小红的想法吗？如果不同意，你认为最多还可以剪出（ ）个图中的三角形。把你的想法在下面写一写，或者在图中画一画。
26．（2023秋·北京延庆·六年级统考期末）同学们玩投包的游戏，在操场上放一个篮筐，参加游戏的同学在篮筐外手拉手围成一个圆，同学们站在圆上投包，看谁投得准。测得一个同学两臂伸平后大约是1.6米。每个同学距篮筐的距离大约是多少米？（得数保留整米数）
27．（2023秋·北京昌平·六年级统考期末）下图是双人花样滑冰运动员中男运动员拉着女运动员做圆周运动的精彩画面。女运动员的冰鞋滑过一周是多少米？（π取3.14）
28．（2022秋·北京丰台·六年级统考期末）六（1）班同学对某小区居民使用共享单车情况调查结果如图。
（1）受访者中“每天必用”和“每周都用几次”的高频次用户共有304人，这次的受访者共有多少人？
（2）受访者中有多少人从来不用共享单车？
29．（2023秋·北京延庆·六年级统考期末）幸福小学开展丰富多彩的体育锻炼活动，下面是根据六（1）班进行“你最喜欢的一项体育活动”调查结果绘制的统计图。
（1）根据两幅图中的相关信息，可以知道六年级（1）班有（ ）人，喜欢足球的人数占全班的（ ）。
（2）先算出喜欢跳绳的人数，再把条形统计图补充完整。
（3）涛涛收集了自己一年级至六年级跳绳个数的数据，为了了解跳绳能力的变化程度，选择（ ）统计图比较合适。
30．（2023秋·北京·六年级统考期末）认真践行“健康第一”的教育理念，帮助学生在体育锻炼中享受乐趣、增强体质、健全人格、锤炼意志，培养学生每天坚持体育锻炼的习惯。张老师开展了“我最喜爱的一项体育活动”的调查，要求每名学生必选且只能选一项。现随机调查了部分学生，并将其结果绘制成如下不完整的条形统计图和扇形统计图。
请结合以上信息解答下列问题：
（1）在这次调查中一共调查了 名学生；
（2）补全条形统计图并标明相应数据；
（3）分析统计图表得到，喜爱 和 项目的人数之和正好占调查总人数的50%；
（4）喜欢跳绳的人数与喜欢羽毛球的人数的比为 ∶ 。
参考答案
1．D
2．D
3．C
4．B
5．C
6．A
7．C
8．D
9．18.28
10． 直角边 重合 到直线外已知点的 直角边 直角符号
11．(1) （4，2） （5，4） （2，4）
(2)（1，5）
12．6
13．20278.8
14．6.28
15．(1)600
(2) 600 800
(3)50
16．快
17．(1) 时间 12
(2) 0 6 6 12
18． 如图：
（答案不唯一）
19． （1）∠1＝150°，∠2＝150°
所以∠1＝∠2。
答：我发现了∠1＝∠2。
（2）因为∠1＋∠3＝180°，∠2＋∠5＝180°
又因为∠1＝∠2，所以∠3＝∠5。
答：∠3＝∠5。
20． ①如图：
②如图：
平行四边形的底＝梯形上底＋梯形下底，平行四边形高＝梯形高
梯形面积＝平行四边形面积÷2＝底×高÷2＝（上底＋下底）×高÷2
21． 由分析可得：“方田章”中求三角形面积方法是“半广以乘正从”，意思就是说，三角形的面积＝底边的一半×高。
22． 由分析可得：后一个顶点所在的位置用数对表示可能为（8，6）
作图如下：
23． （1）我提出的问题是：三角形①的底长多少米？
270×2÷22.5
＝540÷22.5
＝24（米）
答：三角形①的底长24米。
（2）270×2＝540（平方米）是求出了平行四边形的面积；
540÷22.5＝24（米）是求出三角形①的底；
540÷18＝30（米）是求出三角形②的底；
（30＋24）×2＝108（米）是求出平行四边形的周长。
24．
（平方米）
答：可种植部分的面积是128平方米。
25． （1）7×2＝14（平方厘米）
答：长方形的面积是14平方厘米。
（2）如图：
7÷2＝3（个）……1（厘米）
2÷2＝1（个）
1×3×2＝6（个）
6－1＝5（个）
不同意小红的想法，最多还可以剪出5个图中的三角形。
26． 1.6×8＝12.8（米）
12.8÷3.14÷2
≈4÷2
＝2（米）
答：每个同学距篮筐的距离大约是2米。
27． 2×3.14×1.5
＝6.28×1.5
＝9.42（米）
答：女运动员的冰鞋滑过一周是9.42米。
28． （1）304÷（9.5%＋20.9%）
＝304÷30.4%
＝1000（人）
答：这次的受访者共有1000人。
（2）1000×27.8%＝278（人）
答：受访者中有278人从来不用共享单车。
29． （1）
（人）
六年级（1）班有40人，喜欢足球的人数占全班的。
（2）
（人）
作图如下：
（3）涛涛收集了自己一年级至六年级跳绳个数的数据，为了了解跳绳能力的变化程度，选择折线统计图比较合适。
30． （1）21÷14%＝150（名）
在这次调查中一共调查了150名学生。
（2）150－21－39－15－45＝30（名）
条形统计图如下：
（3）喜欢篮球：39÷150×100%
＝0.26×100%
＝26%
喜欢跑步：45÷150×100%
＝0.3×100%
＝30%
喜欢跳绳：15÷150×100%
＝0.1×100%
＝10%
30%＋20%＝50%
根据分析可知，喜爱跑步和足球项目的人数之和正好占调查总人数的50%；
（4）喜欢跳绳的人数与喜欢羽毛球的人数的比：15∶21
＝（15÷3）∶（21÷3）
＝5∶7
喜欢跳绳的人数与喜欢羽毛球的人数的比为5∶7。
成绩
优秀
良好
达标
人数
12
2
4
场次
1
2
3
4
投篮命中率
62.5%
63.2%
58.9%
61.3%