专题03 二次函数中面积问题压轴真题训练-挑战2023年中考数学压轴真题汇编（全国通用）

专题03    二次函数中面积问题压轴真题训练

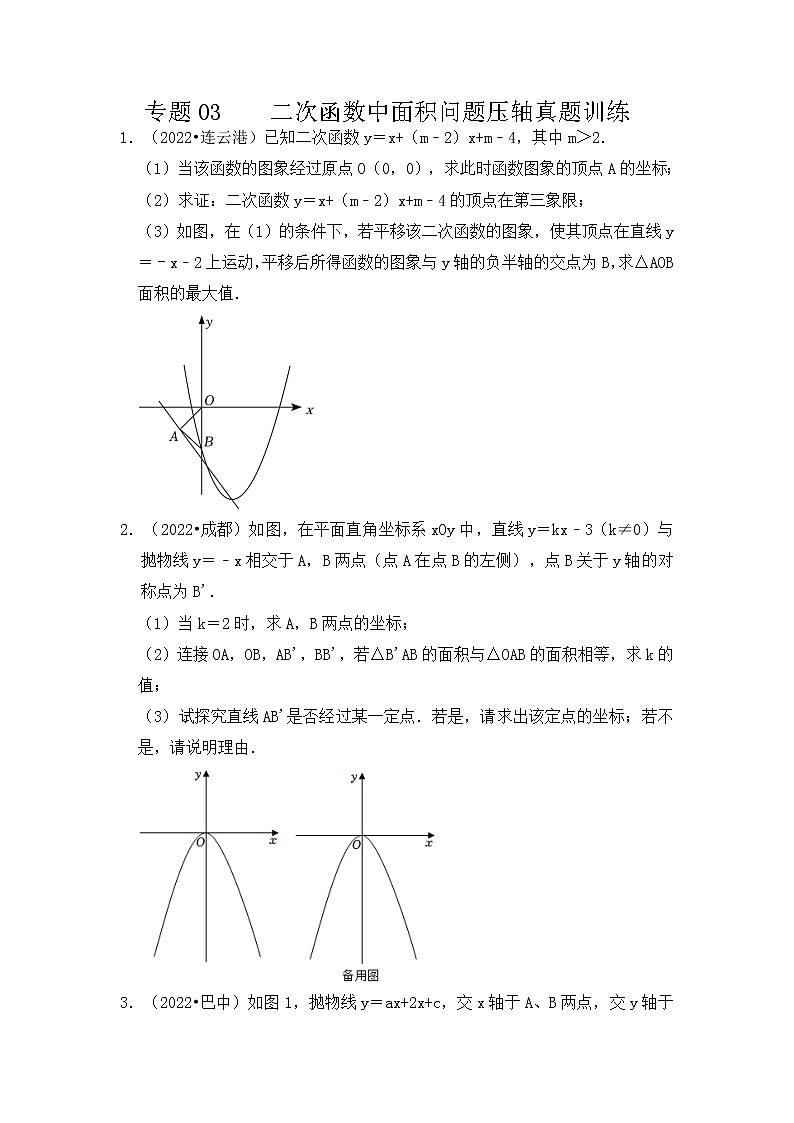
1．（2022•连云港）已知二次函数y＝x+（m﹣2）x+m﹣4，其中m＞2．

（1）当该函数的图象经过原点O（0，0），求此时函数图象的顶点A的坐标；

（2）求证：二次函数y＝x+（m﹣2）x+m﹣4的顶点在第三象限；

（3）如图，在（1）的条件下，若平移该二次函数的图象，使其顶点在直线y＝﹣x﹣2上运动，平移后所得函数的图象与y轴的负半轴的交点为B，求△AOB面积的最大值．

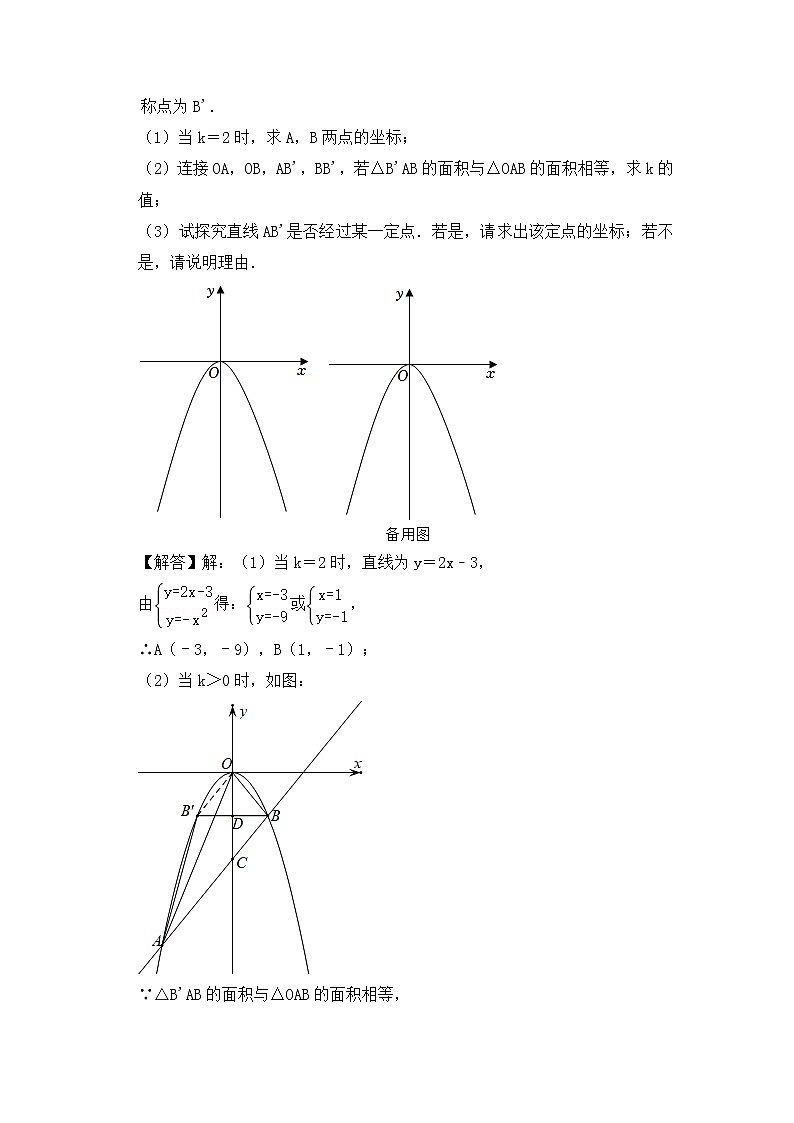
2．（2022•成都）如图，在平面直角坐标系xOy中，直线y＝kx﹣3（k≠0）与抛物线y＝﹣x相交于A，B两点（点A在点B的左侧），点B关于y轴的对称点为B'．

（1）当k＝2时，求A，B两点的坐标；

（2）连接OA，OB，AB'，BB'，若△B'AB的面积与△OAB的面积相等，求k的值；

（3）试探究直线AB'是否经过某一定点．若是，请求出该定点的坐标；若不是，请说明理由．

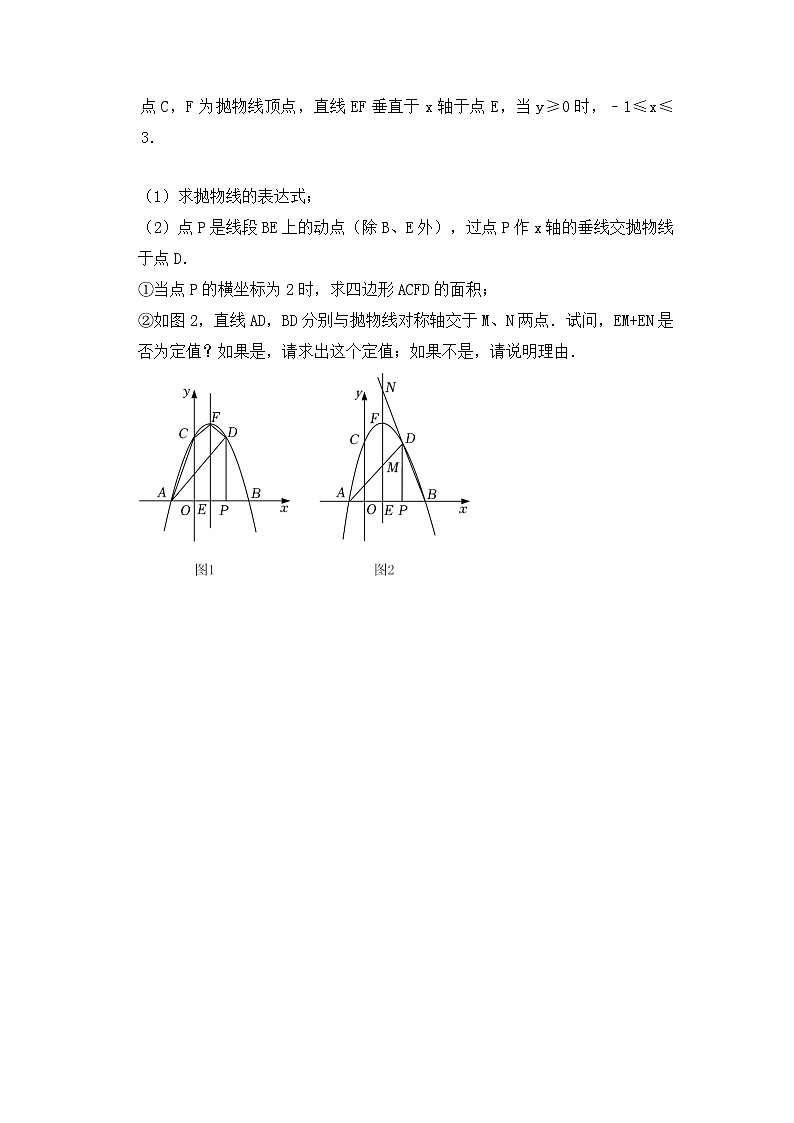
3．（2022•巴中）如图1，抛物线y＝ax+2x+c，交x轴于A、B两点，交y轴于点C，F为抛物线顶点，直线EF垂直于x轴于点E，当y≥0时，﹣1≤x≤3．

（1）求抛物线的表达式；

（2）点P是线段BE上的动点（除B、E外），过点P作x轴的垂线交抛物线于点D．

①当点P的横坐标为2时，求四边形ACFD的面积；

②如图2，直线AD，BD分别与抛物线对称轴交于M、N两点．试问，EM+EN是否为定值？如果是，请求出这个定值；如果不是，请说明理由．

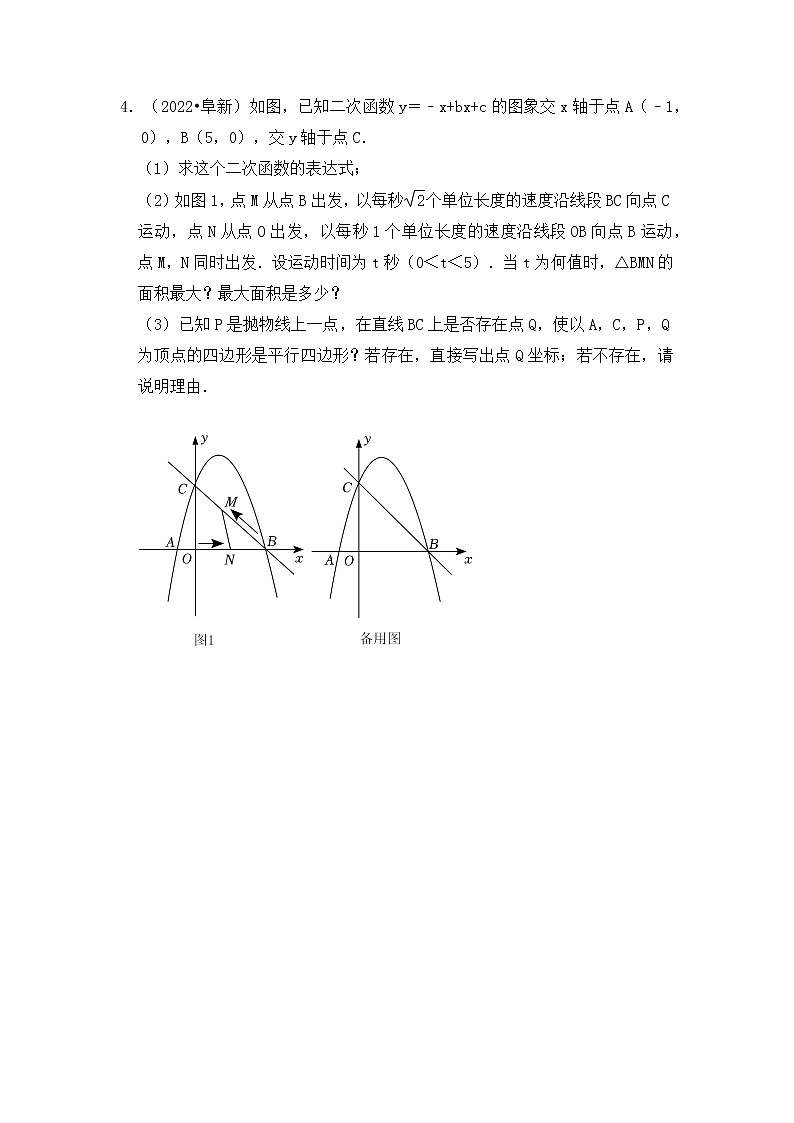
4．（2022•阜新）如图，已知二次函数y＝﹣x+bx+c的图象交x轴于点A（﹣1，0），B（5，0），交y轴于点C．

（1）求这个二次函数的表达式；

（2）如图1，点M从点B出发，以每秒个单位长度的速度沿线段BC向点C运动，点N从点O出发，以每秒1个单位长度的速度沿线段OB向点B运动，点M，N同时出发．设运动时间为t秒（0＜t＜5）．当t为何值时，△BMN的面积最大？最大面积是多少？

（3）已知P是抛物线上一点，在直线BC上是否存在点Q，使以A，C，P，Q为顶点的四边形是平行四边形？若存在，直接写出点Q坐标；若不存在，请说明理由．

5．（2022•鞍山）如图，抛物线y＝﹣x+bx+c与x轴交于A（﹣1，0），B两点，与y轴交于点C（0，2），连接BC．

（1）求抛物线的解析式．

（2）点P是第三象限抛物线上一点，直线PB与y轴交于点D，△BCD的面积为12，求点P的坐标．

（3）在（2）的条件下，若点E是线段BC上点，连接OE，将△OEB沿直线OE翻折得到△OEB'，当直线EB'与直线BP相交所成锐角为45°，时，求点B'的坐标．

6．（2022•菏泽）如图，抛物线y＝ax+bx+c（a≠0）与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点C（0，4），连接AC、BC．

（1）求抛物线的表达式；

（2）将△ABC沿AC所在直线折叠，得到△ADC，点B的对应点为D，直接写出点D的坐标，并求出四边形OADC的面积；

（3）点P是抛物线上的一动点，当∠PCB＝∠ABC时，求点P的坐标．

7．（2022•沈阳）如图，在平面直角坐标系中，抛物线y＝ax+bx﹣3经过点B（6，0）和点D（4，﹣3），与x轴的另一个交点为A，与y轴交于点C，作直线AD．

（1）①求抛物线的函数表达式；

②直接写出直线AD的函数表达式；

（2）点E是直线AD下方的抛物线上一点，连接BE交AD于点F，连接BD，DE，△BDF的面积记为S，△DEF的面积记为S，当S＝2S时，求点E的坐标；

（3）点G为抛物线的顶点，将抛物线图象中x轴下方的部分沿x轴向上翻折，与抛物线剩下的部分组成新的曲线记为C，点C的对应点为C′，点G的对应点为G′，将曲线C沿y轴向下平移n个单位长度（0＜n＜6）．曲线C与直线BC的公共点中，选两个公共点记作点P和点Q，若四边形C′G′QP是平行四边形，直接写出点P的坐标．

8．（2022•西藏）在平面直角坐标系中，抛物线y＝﹣x+（m﹣1）x+2m与x轴交于A，B（4，0）两点，与y轴交于点C，点P是抛物线在第一象限内的一个动点．

（1）求抛物线的解析式，并直接写出点A，C的坐标；

（2）如图甲，点M是直线BC上的一个动点，连接AM，OM，是否存在点M使AM+OM最小，若存在，请求出点M的坐标，若不存在，请说明理由；

（3）如图乙，过点P作PF⊥BC，垂足为F，过点C作CD⊥BC，交x轴于点D，连接DP交BC于点E，连接CP．设△PEF的面积为S，△PEC的面积为S，是否存在点P，使得最大，若存在，请求出点P的坐标，若不存在，请说明理由．

9．（2022•青海）如图1，抛物线y＝x+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．

（1）求该抛物线的解析式；

（2）若点E是抛物线的对称轴与直线BC的交点，点F是抛物线的顶点，求EF的长；

（3）设点P是（1）中抛物线上的一个动点，是否存在满足S＝6的点P？如果存在，请求出点P的坐标；若不存在，请说明理由．（请在图2中探讨）

10．（2022•上海）在平面直角坐标系xOy中，抛物线y＝x+bx+c过点A（﹣2，﹣1），B（0，﹣3）．

（1）求抛物线的解析式；

（2）平移抛物线，平移后的顶点为P（m，n）（m＞0）．

ⅰ．如果S＝3，设直线x＝k，在这条直线的右侧原抛物线和新抛物线均呈上升趋势，求k的取值范围；

ⅱ．点P在原抛物线上，新抛物线交y轴于点Q，且∠BPQ＝120°，求点P的坐标．

11．（2022•福建）在平面直角坐标系xOy中，已知抛物线y＝ax+bx经过A（4，0），B（1，4）两点．P是抛物线上一点，且在直线AB的上方．

（1）求抛物线的解析式；

（2）若△OAB面积是△PAB面积的2倍，求点P的坐标；

（3）如图，OP交AB于点C，PD∥BO交AB于点D．记△CDP，△CPB，△CBO的面积分别为S，S，S．判断+是否存在最大值．若存在，求出最大值；若不存在，请说明理由．

12．（2022•岳阳）如图1，在平面直角坐标系xOy中，抛物线F：y＝x+bx+c经过点A（﹣3，0）和点B（1，0）．

（1）求抛物线F的解析式；

（2）如图2，作抛物线F，使它与抛物线F关于原点O成中心对称，请直接写出抛物线F的解析式；

（3）如图3，将（2）中抛物线F向上平移2个单位，得到抛物线F，抛物线F与抛物线F相交于C，D两点（点C在点D的左侧）．

①求点C和点D的坐标；

②若点M，N分别为抛物线F和抛物线F上C，D之间的动点（点M，N与点C，D不重合），试求四边形CMDN面积的最大值．

13．（2023•沛县模拟）如图，已知抛物线y＝﹣x+ax经过点A（4，0）和B（1，m）点，其对称轴交x轴于点H，点C是抛物线在直线AB上方的一个动点（不含A，B两点）．

（1）求a、m的值．

（2）连接AB、OB，若△AOB的面积是△ABC的面积的2倍，求点C的坐标．

（3）若直线AC、OC分别交该抛物线的对称轴于点E、F，试问EH+FH是否为定值，若是，请求出该定值；若不是，请说明理由．

14．（2023•柳南区一模）如图，已知抛物线的图象经过点C（0，3），与x轴交于A，B两点，顶点坐标D（1，4），连接BC交对称轴于点E．

（1）求抛物线的解析式；

（2）若点P是抛物线上的一个动点，位于直线BC的上方（点P与B，C不重合），过P作y轴的平行线交BC于F点；

①设点P的横坐标为m，当四边形DEFP是平行四边形时，求m的值；

②在①的条件下，抛物线上是否存在点Q，使得△QBC的面积与△PBC的面积相等，若存在，请求出点Q坐标；若不存在，请说明理由．

15．（2022•淄博）如图，抛物线y＝﹣x+bx+c与x轴相交于A，B两点（点A在点B的左侧），顶点D（1，4）在直线l：y＝x+t上，动点P（m，n）在x轴上方的抛物线上．

（1）求这条抛物线对应的函数表达式；

（2）过点P作PM⊥x轴于点M，PN⊥l于点N，当1＜m＜3时，求PM+PN的最大值；

（3）设直线AP，BP与抛物线的对称轴分别相交于点E，F，请探索以A，F，B，G（G是点E关于x轴的对称点）为顶点的四边形面积是否随着P点的运动而发生变化，若不变，求出这个四边形的面积；若变化，说明理由．

16．（2022•烟台）如图，已知直线y＝x+4与x轴交于点A，与y轴交于点C，抛物线y＝ax+bx+c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝﹣1．

（1）求抛物线的表达式；

（2）D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时D点的坐标；

（3）若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．

17．（2022•内江）如图，抛物线y＝ax+bx+c与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．

（1）求这条抛物线所对应的函数的表达式；

（2）若点D为该抛物线上的一个动点，且在直线AC上方，求点D到直线AC的距离的最大值及此时点D的坐标；

（3）点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为1：5两部分，求点P的坐标．

18．（2021•西宁）如图，在平面直角坐标系xOy中，一次函数y＝﹣x+3的图象与x轴交于点A，与y轴交于点B，点C的坐标为（﹣2，0），抛物线经过A，B，C三点．

（1）求抛物线的解析式；

（2）直线AD与y轴负半轴交于点D，且∠BAO＝∠DAO，求证：OB＝OD；

（3）在（2）的条件下，若直线AD与抛物线的对称轴l交于点E，连接BE，在第一象限内的抛物线上是否存在一点P，使四边形BEAP的面积最大？若存在，请求出点P的坐标及四边形BEAP面积的最大值；若不存在，请说明理由．

19．（2021•沈阳）如图，平面直角坐标系中，O是坐标原点，抛物线y＝﹣x+bx+c与x轴交于A、B两点（点A在点B的左侧），点B坐标是（3，0）．抛物线与y轴交于点C（0，3），点P是抛物线的顶点，连接PC．

（1）求抛物线的函数表达式并直接写出顶点P的坐标．

（2）直线BC与抛物线对称轴交于点D，点Q为直线BC上一动点．

①当△QAB的面积等于△PCD面积的2倍时，求点Q的坐标；

②在①的条件下，当点Q在x轴上方时，过点Q作直线l垂直于AQ，直线y＝x﹣交直线l于点F，点G在直线y＝x﹣上，且AG＝AQ时，请直接写出GF的长．

20．（2021•鞍山）如图，抛物线y＝ax+bx﹣3交x轴于点A（﹣1，0），B（3，0），D是抛物线的顶点，P是抛物线上的动点，点P的横坐标为m（0≤m≤3），AE∥PD交直线l：y＝x+2于点E，AP交DE于点F，交y轴于点Q．

（1）求抛物线的表达式；

（2）设△PDF的面积为S，△AEF的面积为S，当S＝S时，求点P的坐标；

（3）连接BQ，点M在抛物线的对称轴上（位于第一象限内），且∠BMQ＝45°，在点P从点B运动到点C的过程中，点M也随之运动，直接写出点M的纵坐标t的取值范围．

21．（2021•辽宁）如图，抛物线y＝﹣x+bx+c与x轴交于点A和点C（﹣1，0），与y轴交于点B（0，3），连接AB，BC，点P是抛物线第一象限上的一动点，过点P作PD⊥x轴于点D，交AB于点E．

（1）求抛物线的解析式；

（2）如图1，作PF⊥PD于点P，使PF＝OA，以PE，PF为邻边作矩形PEGF．当矩形PEGF的面积是△BOC面积的3倍时，求点P的坐标；

（3）如图2，当点P运动到抛物线的顶点时，点Q在直线PD上，若以点Q、A、B为顶点的三角形是锐角三角形，请直接写出点Q纵坐标n的取值范围．