【压轴之满分集训】专题02 函数图像与性质综合题（四大类）-挑战2023年中考数学压轴真题汇编（全国通用）

专题02函数图像与性质综合题（四大类）

【典例分析】

【类型一：分析函数图像】

【典例1】（锦州）已知A，B两地相距10千米，上午9：00甲骑电动车从A地出发到B地，9：10乙开车从B地出发到A地，甲、乙两人距A地的距离y（千米）与甲所用的时间x（分）之间的关系如图所示，则乙到达A地的时间为　  　．

【变式1-1】（2022•潍坊）如图，在▱ABCD中，∠A＝60°，AB＝2，AD＝1，点E，F在▱ABCD的边上，从点A同时出发，分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动，到达点C时停止，线段EF扫过区域的面积记为y，运动时间记为x，能大致反映y与x之间函数关系的图象是（　　）

A． B． 

C． D．

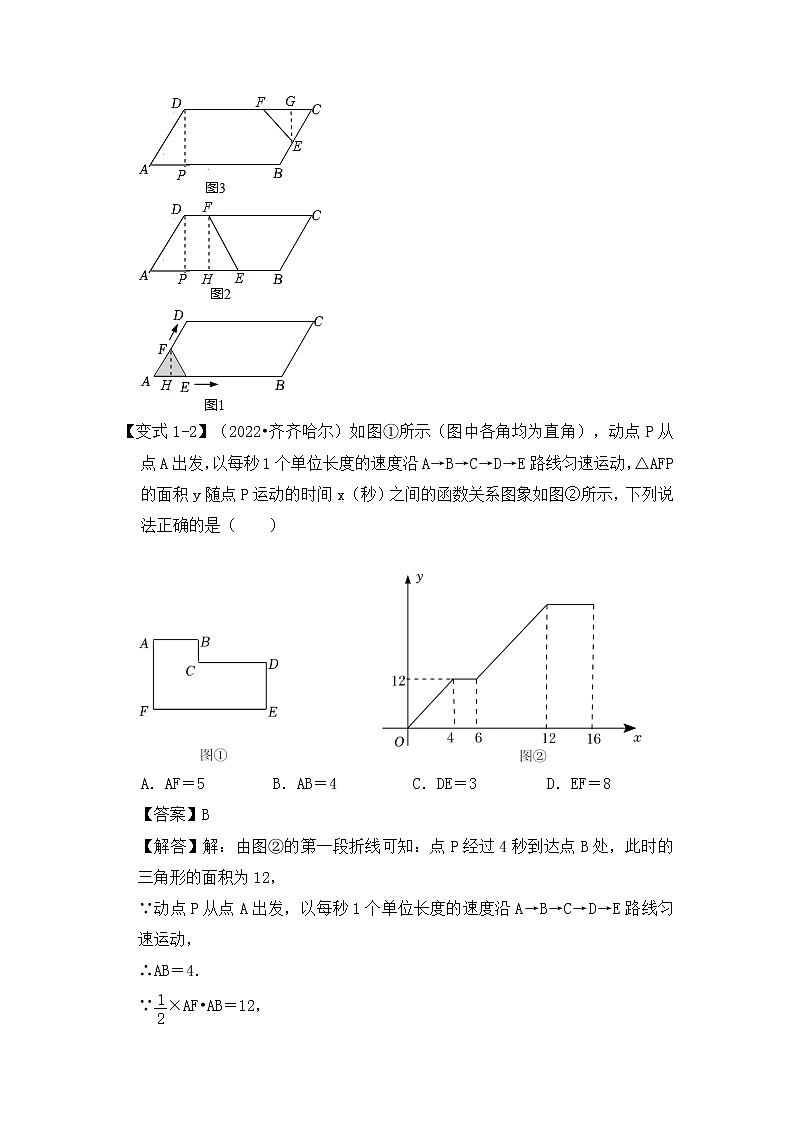
【变式1-2】（2022•齐齐哈尔）如图①所示（图中各角均为直角），动点P从点A出发，以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动，△AFP的面积y随点P运动的时间x（秒）之间的函数关系图象如图②所示，下列说法正确的是（　　）

A．AF＝5 B．AB＝4 C．DE＝3 D．EF＝8

【变式1-3】（2022•宜昌）如图是小强散步过程中所走的路程s（单位：m）与步行时间t（单位：min）的函数图象．其中有一时间段小强是匀速步行的．则这一时间段小强的步行速度为（　　）

A．50m/min B．40m/min C．m/min D．20m/min

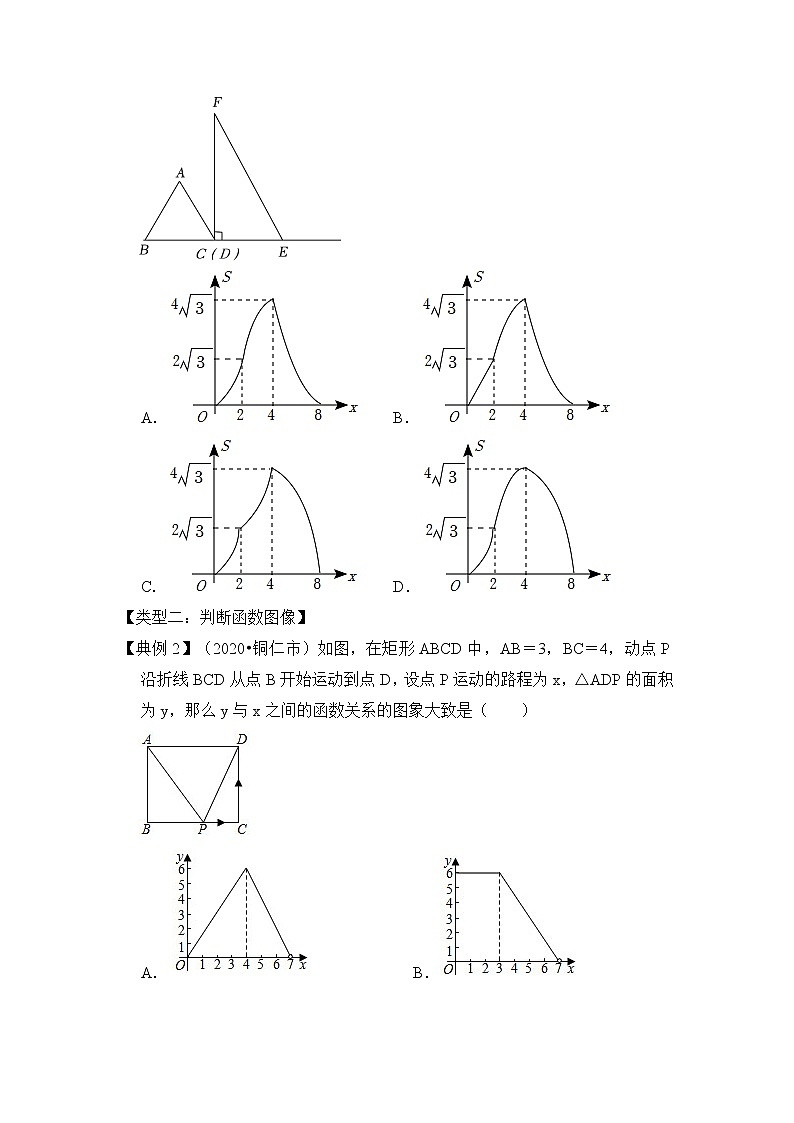
【变式1-4】（2022•辽宁）如图，在等边三角形ABC中，BC＝4，在Rt△DEF中，∠EDF＝90°，∠F＝30°，DE＝4，点B，C，D，E在一条直线上，点C，D重合，△ABC沿射线DE方向运动，当点B与点E重合时停止运动．设△ABC运动的路程为x，△ABC与Rt△DEF重叠部分的面积为S，则能反映S与x之间函数关系的图象是（　　）

A．    B． 

C．    D．

【类型二：判断函数图像】

【典例2】（2020•铜仁市）如图，在矩形ABCD中，AB＝3，BC＝4，动点P沿折线BCD从点B开始运动到点D，设点P运动的路程为x，△ADP的面积为y，那么y与x之间的函数关系的图象大致是（　　）

A． B． 

C． D．

【变式2-1】（2022•湖北）如图，边长分别为1和2的两个正方形，其中有一条边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t，大正方形的面积为S，小正方形与大正方形重叠部分的面积为S，若S＝S﹣S，则S随t变化的函数图象大致为（　　）

A． B． 

C． D．

【变式2-2】（2022•绥化）已知二次函数y＝ax+bx+c的部分函数图象如图所示，则一次函数y＝ax+b﹣4ac与反比例函数y＝在同一平面直角坐标系中的图象大致是（　　）

A． B． 

C． D．

【变式2-3】（2022•广西）已知反比例函数y＝（b≠0）的图象如图所示，则一次函数y＝cx﹣a（c≠0）和二次函数y＝ax+bx+c（a≠0）在同一平面直角坐标系中的图象可能是（　　）

A． B． 

C． D．

【类型三：反比例函数综合】

【典例3】（2022•十堰）如图，正方形ABCD的顶点分别在反比例函数y＝（k＞0）和y＝（k＞0）的图象上．若BD∥y轴，点D的横坐标为3，则k+k＝（　　）

A．36 B．18 C．12 D．9

【变式3-1】（2021•鄂州）如图，点A是反比例函数y＝（x＞0）的图象上一点，过点A作AC⊥x轴于点C，AC交反比例函数y＝（x＞0）的图象于点B，点P是y轴正半轴上一点．若△PAB的面积为2，则k的值为 　　．

【变式3-2】（2021•荆州）如图，过反比例函数y＝（k＞0，x＞0）图象上的四点P，P，P，P分别作x轴的垂线，垂足分别为A，A，A，A，再过P，P，P，P分别作y轴，PA，PA，PA的垂线，构造了四个相邻的矩形．若这四个矩形的面积从左到右依次为S，S，S，S，OA＝AA＝AA＝AA，则S与S的数量关系为 　  　．

【变式3-3】（2022•毕节市）如图，在平面直角坐标系中，正方形ABCD的顶点A，B分别在x轴、y轴上，对角线交于点E，反比例函数y＝（x＞0，k＞0）的图象经过点C，E．若点A（3，0），则k的值是 　　．

【变式3-4】（2022•雁塔区校级模拟）如图，正方形ACBE的边长是，点B，C分别在x轴和y轴正半轴上，BO＝2，ED⊥x轴于点D，ED的中点F在反比例函数y＝（x＞0）的图象上，则k＝　　．

【变式3-5】（2021•广元）如图，点A（﹣2，2）在反比例函数y＝的图象上，点M在x轴的正半轴上，点N在y轴的负半轴上，且OM＝ON＝5．点P（x，y）是线段MN上一动点，过点A和P分别作x轴的垂线，垂足为点D和E，连接OA、OP．当S＜S时，x的取值范围是 　   　．

【变式3-6】（2021•荆门）如图，在平面直角坐标系中，Rt△OAB斜边上的高为1，∠AOB＝30°，将Rt△OAB绕原点顺时针旋转90°得到Rt△OCD，点A的对应点C恰好在函数y＝（k≠0）的图象上，若在y＝的图象上另有一点M使得∠MOC＝30°，则点M的坐标为 　   　．

【变式3-7】（2021•达州）如图，将一把矩形直尺ABCD和一块等腰直角三角板EFG摆放在平面直角坐标系中，AB在x轴上，点G与点A重合，点F在AD上，EF交BC于点M，反比例函数y＝（x＜0）的图象恰好经过点F，M，若直尺的宽CD＝1，三角板的斜边FG＝4，则k＝　  　．

【类型4：二次函数综合】

【典例4】（2021•广安）二次函数y＝ax+bx+c（a≠0）的图象如图所示，有下列结论：①abc＞0，②4a﹣2b+c＜0，③a﹣b≥x（ax+b），④3a+c＜0，正确的有（　　）

A．1个 B．2个 C．3个 D．4个

【变式4-1】（2022•辽宁）抛物线y＝ax+bx+c的部分图象如图所示，对称轴为直线x＝﹣1，直线y＝kx+c与抛物线都经过点（﹣3，0）．下列说法：①ab＞0；②4a+c＞0；③若（﹣2，y）与（，y）是抛物线上的两个点，则y＜y；④方程ax+bx+c＝0的两根为x＝﹣3，x＝1；⑤当x＝﹣1时，函数y＝ax+（b﹣k）x有最大值．其中正确的个数是（　　）

A．2 B．3 C．4 D．5

【变式4-2】（2022•烟台）二次函数y＝ax+bx+c（a≠0）的部分图象如图所示，其对称轴为直线x＝﹣，且与x轴的一个交点坐标为（﹣2，0）．下列结论：①abc＞0；②a＝b；③2a+c＝0；④关于x的一元二次方程ax+bx+c﹣1＝0有两个相等的实数根．其中正确结论的序号是（　　）

A．①③ B．②④ C．③④ D．②③

【变式4-3】（2022•梧州）如图，已知抛物线y＝ax+bx﹣2的对称轴是直线x＝﹣1，直线l∥x轴，且交抛物线于点P（x，y），Q（x，y），下列结论错误的是（　　）

A．b＞﹣8a 

B．若实数m≠﹣1，则a﹣b＜am+bm 

C．3a﹣2＞0 

D．当y＞﹣2时，x•x＜0

【变式4-4】（2022•天津）已知抛物线y＝ax+bx+c（a，b，c是常数，0＜a＜c）经过点（1，0），有下列结论：

①2a+b＜0；

②当x＞1时，y随x的增大而增大；

③关于x的方程ax+bx+（b+c）＝0有两个不相等的实数根．

其中，正确结论的个数是（　　）

A．0 B．1 C．2 D．3

【变式4-5】（2021•福建）二次函数y＝ax﹣2ax+c（a＞0）的图象过A（﹣3，y），B（﹣1，y），C（2，y），D（4，y）四个点，下列说法一定正确的是（　　）

A．若yy＞0，则yy＞0 B．若yy＞0，则yy＞0 

C．若yy＜0，则yy＜0 D．若yy＜0，则yy＜0

【变式4-6】（2021•恩施州）如图，已知二次函数y＝ax+bx+c的图象与x轴交于（﹣3，0），顶点是（﹣1，m），则以下结论：①abc＞0；②4a+2b+c＞0；③若y≥c，则x≤﹣2或x≥0；④b+c＝m．其中正确的有（　　）个．

A．1 B．2 C．3 D．4