中考数学一轮复习课时练习课件课时35 圆的基本性质二 (含答案)

这是一份中考数学一轮复习课时练习课件课时35 圆的基本性质二 (含答案)，共26页。PPT课件主要包含了同一个圆等内容，欢迎下载使用。

考点一　 弧、弦、圆心角的关系【主干必备】
【微点警示】 1.圆心角与所对弧的度数相等.2.弧、弦、圆心角的关系必须在同圆或等圆中应用.
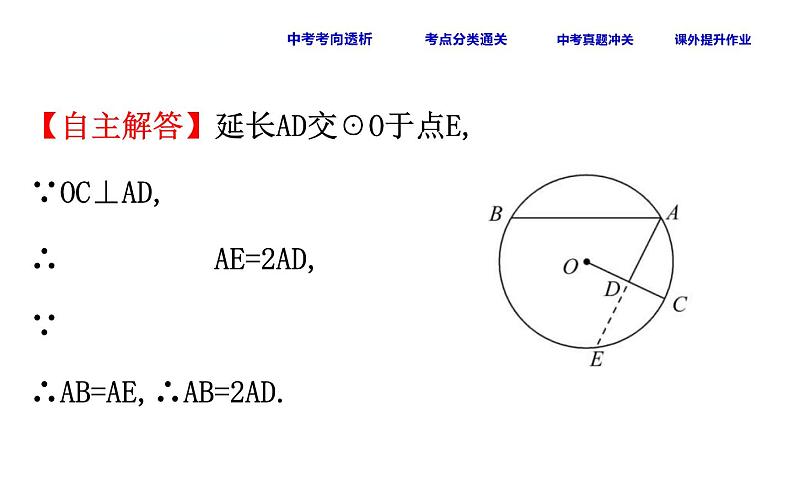
【核心突破】【例1】(2018·牡丹江中考)如图,在☉O中, AD⊥OC于点D.求证:AB=2AD.
【自主解答】延长AD交☉O于点E,∵OC⊥AD,∴ AE=2AD,∵ ∴AB=AE,∴AB=2AD.
【明·技法】应用弧、弦、圆心角的关系时的两点注意1.不能忽略“在同圆或等圆中”这个前提条件,不在同圆或等圆中的圆心角相等,所对的弧、弦不一定相等.
2.因为一条弦所对的弧有两条,所以由“弦等”得出“弧等”时,应指明劣弧和劣弧相等,优弧和优弧相等.
【题组过关】1.如图,在☉O中,OA⊥OB,∠A=35°,则 所对圆心角的度数为世纪金榜导学号(　 　)A.20°　　　B.25°　　　C.30°　　　D.35°
2.(2019·天津南开区模拟)如图,在☉O中,AB,CD是两条弦,OM⊥CD,ON⊥AB,如果AB=CD,则下列结论不正确的是(　 　)A.∠AON=∠DOM B.AN=DMC.OM=DM D.OM=ON
3.(2019·上海嘉定区一模)如图,在圆O中,AB是弦,点C是劣弧 的中点,连接OC,AB平分OC,连接OA、OB,那么∠AOB=________度.世纪金榜导学号 
考点二　圆周角定理及推论【主干必备】
【微点警示】 1.顶点在圆上的角不一定是圆周角.2.圆周角定理必须在同圆或等圆中应用.
【核心突破】【例2】(2019·滨州中考)如图,AB为☉O的直径,C,D为☉O上两点,若∠BCD=40°,则∠ABD的大小为(　 　)　　　　　　　　　　　　　　　　　　A.60°B.50°C.40°D.20°
【明·技法】圆周角定理及推论的应用1.由于直径所对的圆周角是直角,所以在圆中,有直径时,构造直径所对的圆周角,利用解直角三角形的知识解决问题.这是圆中最常用的辅助线.2.在圆中,常利用等弧所对的圆周角相等证明角相等.
【题组过关】1.(2019·济南历下区期末)如图,AB是☉O的直径,点C在☉O上,∠ABC=30°,AC=4,则☉O的半径为(　 　)A.4　　　B.8　　　C.2 　　　D.4
2.(2019·泰州高港区期末)如图,AB为☉O的直径,点C,D在☉O上,若∠C=110°,则∠AOD等于(　 　)A.35°　　　B.40°　　　C.45°　　　D.70°
3.如图,☉O是正方形ABCD的外接圆,若点P在☉O上且与A,B不重合,则∠APB的大小为_______度.世纪金榜导学号 
4.(2019·武昌模拟)如图,BE是☉O的直径,半径OA⊥弦BC,点D为垂足,连接AE,EC.世纪金榜导学号(1)若∠AEC=28°,求∠AOB的度数.(2)若∠BEA=∠B,EC=3,求☉O的半径.略
考点三　圆内接四边形【主干必备】
【微点警示】 1.圆内接四边形的四个顶点都在同一个圆上.2.圆内接四边形的性质是反映对角的关系.
【核心突破】【例3】(2018·邵阳中考)如图所示,四边形ABCD为☉O的内接四边形,∠BCD=120°,则∠BOD的大小是(　 　)A.80°　　　 B.120°C.100° D.90°
【明·技法】圆内接四边形的角的“两种”关系1.对角互补,若四边形ABCD为☉O的内接四边形,则∠A+∠C=180°,∠B+∠D=180°.2.任一外角与其相邻的内角的对角相等,简称圆内接四边形的外角等于其内对角.
【题组过关】1.(2019·天津和平区期末)如图,四边形ABCD内接于☉O,AB是☉O的直径,若∠BAC=20°,则∠ADC的度数是(　 　)A.90°　　　B.100°　　　C.110°　　　D.130°
2.如图,点A,B,C,D,E都是☉O上的点, ∠B=118°,则∠D的度数为世纪金榜导学号(　 　)A.122°B.124°C.126°D.128°