数学九年级上册湖北省襄阳市老河口市九年级（上）期中数学试卷

这是一份数学九年级上册湖北省襄阳市老河口市九年级（上）期中数学试卷，共20页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
湖北省襄阳市老河口市九年级（上）期中数学试卷
　
一、选择题（共10小题，每小题3分，满分30分）
1．（3分）方程x2﹣x=0的解是（　　）
A．x=0 B．x=1 C．x1=0，x2=﹣1 D．x1=0，x2=1
2．（3分）一元二次方程4x2+1=4x的根的情况是（　　）
A．没有实数根 B．只有一个实数根
C．有两个相等的实数根 D．有两个不相等的实数根
3．（3分）下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）
A． B． C． D．
4．（3分）抛物线y=﹣x2+2x+3的顶点坐标是（　　）
A．（﹣1，4） B．（1，3） C．（﹣1，3） D．（1，4）
5．（3分）如图，A、B、C是⊙O上的三点，∠BOC=70°，则∠A的度数为（　　）

A．70° B．45° C．40° D．35°
6．（3分）某养殖户的养殖成本逐年增长，第一年的养殖成本为12万元，第3年的养殖成本为16万元．设养殖成本平均每年增长的百分率为x，则下面所列方程中正确的是（　　）
A．12（1﹣x）2=16 B．16（1﹣x）2=12 C．16（1+x）2=12 D．12（1+x）2=16
7．（3分）已知二次函数y=﹣（x+k）2+h，当x＞﹣2时，y随x的增大而减小，则函数中k的取值范围是（　　）
A．k≥﹣2 B．k≤﹣2 C．k≥2 D．k≤2
8．（3分）⊙O的直径为10，圆心O到弦AB的距离为3，则弦AB的长是（　　）
A．4 B．6 C．7 D．8
9．（3分）在△ABC中，∠A=90°，AB=3cm，AC=4cm，若以A为圆心3cm为半径作⊙O，则BC与⊙O的位置关系是（　　）
A．相交 B．相离 C．相切 D．不能确定
10．（3分）二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴为x=1，给出下列结论：①abc＞0；②当x＞2时，y＞0；③3a+c＞0；④3a+b＞0．其中正确的结论有（　　）

A．①② B．①④ C．①③④ D．②③④
　
二．填空题：（本大题共6个小题，每小题3分，共18分．把答案填在答题卡的相应位置上．）
11．（3分）若x=1是一元二次方程x2+2x+a=0的一根，则另一根为　　．
12．（3分）将一抛物线先向右平移1个单位，再向上平移2个单位后，得到的抛物线的解析式是y=x2﹣2x，则原抛物线的解析式是　　．
13．（3分）如图，将△AOB绕点O顺时针旋转36°得△COD，AB与其对应边CD相交所构成的锐角的度数是　　．

14．（3分）在某次聚会上，每两人都握了一次手，所有人共握手36次，参加这次聚会的有　　人．
15．（3分）已知二次函数y=x2+bx+c的图象过点A（1，m），B（3，m），若点M（﹣2，y1），N（﹣1，y2），K（8，y3）也在二次函数y=x2+bx+c的图象上，将y1，y2，y3按从小到大的顺序用“＜”连接，结果是　　．
16．（3分）如图，⊙O的直径CD与弦AB垂直相交于点E，且BC=1，AD=2，则⊙O的直径长为　　．

　
三、解答题（共9小题，满分72分）
17．（6分）解方程：x2﹣x﹣=0．
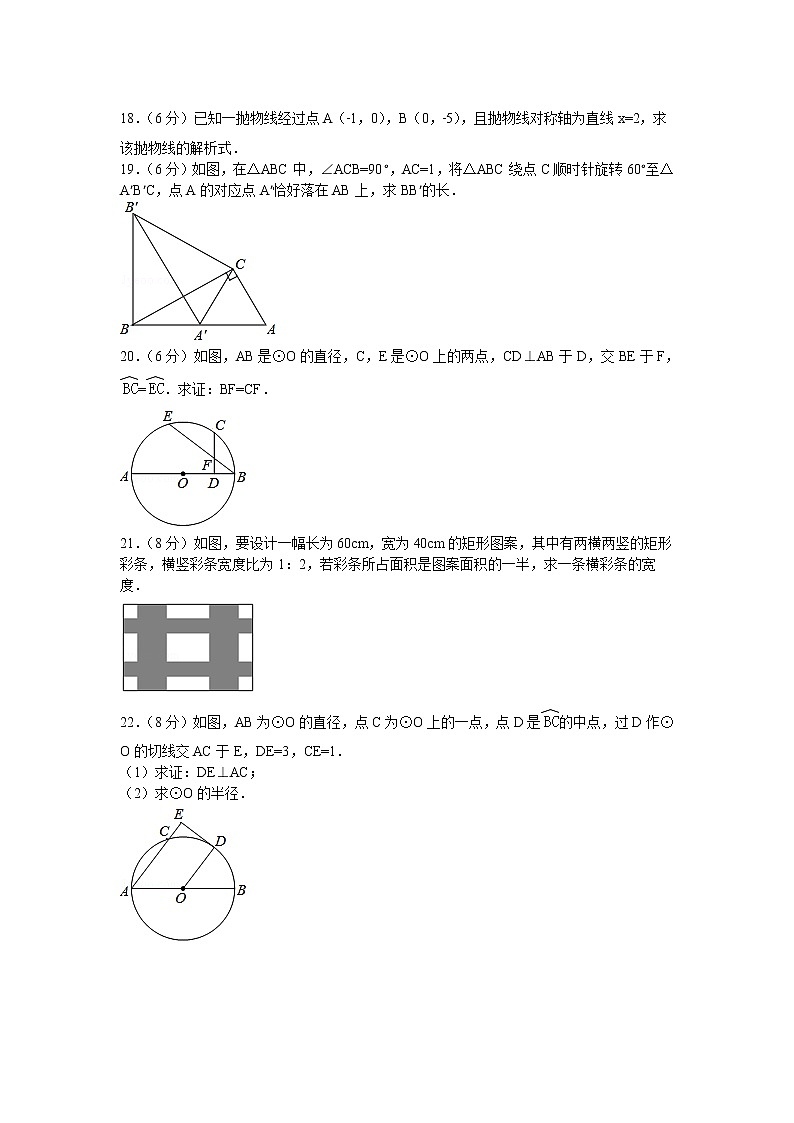
18．（6分）已知一抛物线经过点A（﹣1，0），B（0，﹣5），且抛物线对称轴为直线x=2，求该抛物线的解析式．
19．（6分）如图，在△ABC中，∠ACB=90°，AC=1，将△ABC绕点C顺时针旋转60°至△A′B′C，点A的对应点A′恰好落在AB上，求BB′的长．

20．（6分）如图，AB是⊙O的直径，C，E是⊙O上的两点，CD⊥AB于D，交BE于F，=．求证：BF=CF．

21．（8分）如图，要设计一幅长为60cm，宽为40cm的矩形图案，其中有两横两竖的矩形彩条，横竖彩条宽度比为1：2，若彩条所占面积是图案面积的一半，求一条横彩条的宽度．

22．（8分）如图，AB为⊙O的直径，点C为⊙O上的一点，点D是的中点，过D作⊙O的切线交AC于E，DE=3，CE=1．
（1）求证：DE⊥AC；
（2）求⊙O的半径．

23．（10分）某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=﹣x+140，该商场销售这种服装获得利润为w元．
（1）求w与x之间的函数关系式；
（2）销售单价定为多少时，商场可获得最大利润？最大利润是多少元？
（3）若该商场想要获得不低于700元的利润，试确定销售单价x的范围．
24．（10分）如图，在等边△ABC中，点D为△ABC内的一点，∠ADB=120°，∠ADC=90°，将△ABD绕点A逆时针旋转60°得△ACE，连接DE．
（1）求证：AD=DE；
（2）求∠DCE的度数；
（3）若BD=1，求AD，CD的长．

25．（12分）如图，抛物线y=（x﹣1）2+n与x轴交于A，B两点（A在B的左侧），与y轴交于点C（0，﹣3），点D与点C关于抛物线的对称轴对称．
（1）求抛物线的解析式及点D的坐标；
（2）点P是抛物线对称轴上的一动点，当△PAC的周长最小时，求出点P的坐标；
（3）点Q在x轴上，且∠ADQ=∠DAC，请直接写出点Q的坐标．

　

湖北省襄阳市老河口市九年级（上）期中数学试卷
参考答案与试题解析
　
一、选择题（共10小题，每小题3分，满分30分）
1．（3分）（2014•抚顺一模）方程x2﹣x=0的解是（　　）
A．x=0 B．x=1 C．x1=0，x2=﹣1 D．x1=0，x2=1
【分析】先把方程左边分解，这样把原方程化为x=0或x﹣1=0，然后解一次方程即可．
【解答】解：x（x﹣1）=0，
x=0或x﹣1=0，
所以x1=0，x2=1．
故选D．
【点评】本题考查了解一元二次方程﹣因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．
　
2．（3分）（2015•滨州）一元二次方程4x2+1=4x的根的情况是（　　）
A．没有实数根 B．只有一个实数根
C．有两个相等的实数根 D．有两个不相等的实数根
【分析】先求出△的值，再判断出其符号即可．
【解答】解：原方程可化为：4x2﹣4x+1=0，
∵△=42﹣4×4×1=0，
∴方程有两个相等的实数根．
故选C．
【点评】本题考查的是根的判别式，熟知一元二次方程ax2+bx+c=0（a≠0）的根与△的关系是解答此题的关键．
　
3．（3分）（2016•曲阜市校级自主招生）下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）
A． B． C． D．
【分析】根据中心对称图形的概念求解即可．
【解答】解：A、不是中心对称图形，本选项错误；
B、不是中心对称图形，本选项错误；
C、不是中心对称图形，本选项错误；
D、是中心对称图形，本选项正确．
故选D．
【点评】本题考查了中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180度后两部分重合．
　
4．（3分）（2014•惠山区校级模拟）抛物线y=﹣x2+2x+3的顶点坐标是（　　）
A．（﹣1，4） B．（1，3） C．（﹣1，3） D．（1，4）
【分析】已知抛物线的解析式是一般式，用配方法转化为顶点式，根据顶点式的坐标特点，直接写出顶点坐标．
【解答】解：∵y=﹣x2+2x+3=﹣（x2﹣2x+1）+1+3=﹣（x﹣1）2+4，
∴抛物线y=﹣x2+2x+3的顶点坐标是（1，4）．
故选D．
【点评】此题考查了二次函数的性质，二次函数y=a（x﹣h）2+k的顶点坐标为（h，k），对称轴为x=h，此题还考查了配方法求顶点式．
　
5．（3分）（2012•海曙区模拟）如图，A、B、C是⊙O上的三点，∠BOC=70°，则∠A的度数为（　　）

A．70° B．45° C．40° D．35°
【分析】由A、B、C是⊙O上的三点，∠BOC=70°，根据在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，即可求得答案．
【解答】解：∵A、B、C是⊙O上的三点，∠BOC=70°，
∴∠A=∠BOC=35°．
故选D．
【点评】此题考查了圆周角定理．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半定理的应用是解此题的关键．
　
6．（3分）（2016秋•老河口市期中）某养殖户的养殖成本逐年增长，第一年的养殖成本为12万元，第3年的养殖成本为16万元．设养殖成本平均每年增长的百分率为x，则下面所列方程中正确的是（　　）
A．12（1﹣x）2=16 B．16（1﹣x）2=12 C．16（1+x）2=12 D．12（1+x）2=16
【分析】解决此类两次变化问题，可利用公式a（1+x）2=c，那么两次涨价后售价为12（1+x）2，然后根据题意可得出方程．
【解答】解：根据题意可列方程：12（1+x）2=16，
故选：D．
【点评】本题考查一元二次方程的应用，解决此类两次变化问题，可利用公式a（1+x）2=c，其中a是变化前的原始量，c是两次变化后的量，x表示平均每次的增长率．
　
7．（3分）（2015•新乐市一模）已知二次函数y=﹣（x+k）2+h，当x＞﹣2时，y随x的增大而减小，则函数中k的取值范围是（　　）
A．k≥﹣2 B．k≤﹣2 C．k≥2 D．k≤2
【分析】先利用二次函数的性质求出抛物线的对称轴为直线x=﹣k，则当x＞﹣k时，y的值随x值的增大而减小，由于x＞﹣2时，y的值随x值的增大而减小，于是得到﹣k≤﹣2，再解不等式即可．
【解答】解：抛物线的对称轴为直线x=﹣k，
因为a=﹣1＜0，
所以抛物线开口向下，
所以当x＞﹣k时，y的值随x值的增大而减小，
而x＞﹣2时，y的值随x值的增大而减小，
所以﹣k≤﹣2，
所以k≥2．
故选C．
【点评】本题考查了二次函数的性质：二次函数y=ax2+bx+c（a≠0）的顶点坐标是（﹣，），对称轴直线x=﹣，二次函数y=ax2+bx+c（a≠0）的图象具有如下性质：当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，x＜﹣时，y随x的增大而减小；x＞﹣时，y随x的增大而增大；x=﹣时，y取得最小值，即顶点是抛物线的最低点．当a＜0时，抛物线y=ax2+bx+c（a≠0）的开口向下，x＜﹣时，y随x的增大而增大；x＞﹣时，y随x的增大而减小；x=﹣时，y取得最大值，即顶点是抛物线的最高点．
　
8．（3分）（2016秋•宜昌期中）⊙O的直径为10，圆心O到弦AB的距离为3，则弦AB的长是（　　）
A．4 B．6 C．7 D．8
【分析】先求出半径，再利用勾股定理求出半弦长，弦长就可以求出了．
【解答】解：如图，根据题意得，
∵OA=×10=5，AE===4
∴AB=2AE=8．
故选D．

【点评】本题考查的是垂径定理，根据题意画出图形，作出辅助线，构造出直角三角形是解答此题的关键．
　
9．（3分）（2015•岳池县模拟）在△ABC中，∠A=90°，AB=3cm，AC=4cm，若以A为圆心3cm为半径作⊙O，则BC与⊙O的位置关系是（　　）
A．相交 B．相离 C．相切 D．不能确定
【分析】首先求出点A与直线BC的距离，根据直线与圆的位置关系得出BC与⊙O的位置关系．
【解答】解：做AD⊥BC，
∵∠A=90°，AB=3cm，AC=4cm，若以A为圆心3cm为半径作⊙O，
∴BC=5，
∴AD×BC=AC×AB，
解得：AD=2.4，2.4＜3，
∴BC与⊙O的位置关系是：相交．
故选A．

【点评】此题主要考查了直线与圆的位置关系，正确得出点与直线的距离是确定点与直线的距离，是解决问题的关键．
　
10．（3分）（2016秋•老河口市期中）二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴为x=1，给出下列结论：①abc＞0；②当x＞2时，y＞0；③3a+c＞0；④3a+b＞0．其中正确的结论有（　　）

A．①② B．①④ C．①③④ D．②③④
【分析】根据二次函数的图象的开口向上可得a＞0，根据图象y轴的交点在y轴的交点可得c＜0，根据对称轴是直线x=1可得b＜0，进而可得①正确，再根据函数图象可得x＞2时，y有小于0的情况，故②错误，再计算出当x=1时，a﹣b+c＞0，再结合对称轴可得2a+b=0，进而可得3a+c＞0；再由2a+b=0，a＞0可得3a+b＞0．
【解答】解：∵二次函数的图象的开口向上，
∴a＞0，
∵二次函数的图象y轴的交点在y轴的负半轴上，
∴c＜0，
∵二次函数图象的对称轴是直线x=1，
∴﹣=1，
∴2a+b=0，b＜0，
∴abc＞0，∴①正确；
∵二次函数y=ax2+bx+c图象可知，当x＞2时，y有小于0的情况，
∴②错误；
∵当x=﹣1时，y＞0，
∴a﹣b+c＞0，
把b=﹣2a代入得：3a+c＞0，
∴③正确；
∵二次函数图象的对称轴是直线x=1，
∴﹣=1，
∴2a+b=0，
∵a＞0，
∴3a+b＞0，故④正确．
故选C．
【点评】此题考查了二次函数图象与系数的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，关键是数熟练掌握二次函数的性质．
　
二．填空题：（本大题共6个小题，每小题3分，共18分．把答案填在答题卡的相应位置上．）
11．（3分）（2016秋•老河口市期中）若x=1是一元二次方程x2+2x+a=0的一根，则另一根为　﹣3　．
【分析】设方程的另外一根为m，根据根与系数的关系可得出关于m的一元一次方程，解方程即可得出结论．
【解答】解：设方程的另外一根为m，
则有：1+m=﹣2，
解得：m=﹣3．
故答案为：﹣3．
【点评】本题考查了根与系数的关系，熟练掌握两根之和为﹣是解题的关键．
　
12．（3分）（2016秋•老河口市期中）将一抛物线先向右平移1个单位，再向上平移2个单位后，得到的抛物线的解析式是y=x2﹣2x，则原抛物线的解析式是　y=x2﹣3　．
【分析】根据图象反向平移，可得原函数图象，根据图象左加右减，上加下减，可得答案．
【解答】解：一抛物线向右平移1个单位，再向上平移2个单位后所得抛物线的表达式为y=x2﹣2x，
抛物线的表达式为y=x2﹣2x=（x﹣1）2﹣1，左移一个单位，下移2个单位得原函数解析式y=（x﹣1+1）2﹣1﹣2，即y=x2﹣3
故答案为：y=x2﹣3．
【点评】本题考查了二次函数图象与几何变换，利用了图象左加右减，上加下减的规律．
　
13．（3分）（2016秋•老河口市期中）如图，将△AOB绕点O顺时针旋转36°得△COD，AB与其对应边CD相交所构成的锐角的度数是　36°　．

【分析】如图，设AB与OC交于点H，AN与CD交于点E．利用三角形内角和定理即可证明
【解答】解：如图，设AB与OC交于点H，AN与CD交于点E．

∵∠A=∠C，∠AOH=36°，
∵∠AHO=∠CHE，∠A+∠AHO+∠AOH=180°，∠C+∠CHB+∠CEH=180°，
∴∠AOH=∠CEH=36°．
故答案为36°；
【点评】本题考查旋转的性质、三角形内角和定理等知识，解题的关键是灵活应用旋转不变性解决问题，属于中考常考题型．
　
14．（3分）（2016秋•老河口市期中）在某次聚会上，每两人都握了一次手，所有人共握手36次，参加这次聚会的有　9　人．
【分析】设参加这次聚会的有x人，每个人都与另外的人握手一次，则每个人握手（x﹣1）次，且其中任何两人的握手只有一次，因而共有x（x﹣1）次，设出未知数列方程解答即可．
【解答】解：设参加这次聚会的有x人，根据题意列方程得，
x（x﹣1）=36，
解得x1=9，x2=﹣8（不合题意，舍去）；
答：参加这次聚会的有9人．
故答案为9．
【点评】此题主要考查一元二次方程的应用，理解：设有x人参加聚会，每个人都与另外的人握手一次，则每个人握手（x﹣1）次是关键．
　
15．（3分）（2016秋•老河口市期中）已知二次函数y=x2+bx+c的图象过点A（1，m），B（3，m），若点M（﹣2，y1），N（﹣1，y2），K（8，y3）也在二次函数y=x2+bx+c的图象上，将y1，y2，y3按从小到大的顺序用“＜”连接，结果是　y2＜y1＜y3　．
【分析】利用A点与B点为抛物线上的对称点得到对称轴为直线x=2，然后根据点M、N、K离对称轴的远近求解．
【解答】解：∵二次函数y=x2+bx+c的图象过点A（1，m），B（3，m），
∴抛物线开口向上，对称轴为直线x=2，
∵M（﹣2，y1），N（﹣1，y2），K（8，y3），
∴K点离对称轴最远，N点离对称轴最近，
∴y2＜y1＜y3．
故选B．y2＜y1＜y3；
【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标特征满足其解析式．
　
16．（3分）（2016秋•老河口市期中）如图，⊙O的直径CD与弦AB垂直相交于点E，且BC=1，AD=2，则⊙O的直径长为　　．

【分析】连接AC，由CD与AB垂直，利用垂径定理得到AE=BE，进而确定出AC=BC，在直角三角形ACD中，利用勾股定理求出CD的长即可．
【解答】解：连接AC，
∵直径CD⊥AB，
∴AE=BE，
∴AC=BC=1，
在Rt△ACD中，AD=2，AC=1，
根据勾股定理得：CD==，
故答案为：
【点评】此题考查了垂径定理，勾股定理，熟练掌握垂径定理是解本题的关键．
　
三、解答题（共9小题，满分72分）
17．（6分）（2016秋•老河口市期中）解方程：x2﹣x﹣=0．
【分析】先计算判别式的值，然后利用求根公式求方程的解．
【解答】解：△=（﹣1）2﹣4×1×（﹣）=8，
x==，
所以x1=，x2=．
【点评】本题考查了解一元二次方程﹣公式法：用求根公式解一元二次方程的方法是公式法．
　
18．（6分）（2016秋•老河口市期中）已知一抛物线经过点A（﹣1，0），B（0，﹣5），且抛物线对称轴为直线x=2，求该抛物线的解析式．
【分析】因为对称轴是直线x=2，所以得到点（﹣1，0）的对称点是（5，0），因此利用交点式y=a（x﹣x1）（x﹣x2），求出解析式．
【解答】解：∵抛物线对称轴是直线x=2且经过点（﹣1，0），
由抛物线的对称性可知：抛物线还经过点（5，0），
设抛物线的解析式为y=a（x﹣x1）（x﹣x2）（a≠0），
即：y=a（x+1）（x﹣5），
把B（0，﹣5）代入得：﹣5=﹣5a，
∴a=1．
∴抛物线的解析式为：y=x2﹣4x﹣5．
【点评】本题考查了用待定系数法求函数解析式的方法，注意选择若知道与x轴的交点坐标，采用交点式比较简单．
　
19．（6分）（2016秋•老河口市期中）如图，在△ABC中，∠ACB=90°，AC=1，将△ABC绕点C顺时针旋转60°至△A′B′C，点A的对应点A′恰好落在AB上，求BB′的长．

【分析】先利用旋转的性质得CA=CA′，CB=CB′，∠ACA′=∠BCB′=60°，则可判断△ACA′和△BCB′均为等边三角形，于是得到BB′=BC，∠A=60°，∠CBB′=60°，接着计算出∠ABC=90°﹣∠A=30°，则可计算出BC的长，从而得到BB′的长．
【解答】解：∵将△ABC绕点C顺时针旋转60°至△A′B′C，
∴CA=CA′，CB=CB′，∠ACA′=∠BCB′=60°，
∴△ACA′和△BCB′均为等边三角形，
∴BB′=BC，∠A=60°，∠CBB′=60°，
∵点A′在AB上，∠ACB=90°，
∴∠A=60°，∠ABC=90°﹣∠A=30°，
在Rt△ABC中，BC=CA=，
∴BB′=．
【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
　
20．（6分）（2016秋•老河口市期中）如图，AB是⊙O的直径，C，E是⊙O上的两点，CD⊥AB于D，交BE于F，=．求证：BF=CF．

【分析】延长CD交⊙O于点G，连接BC，根据垂径定理证明即可．
【解答】证明：延长CD交⊙O于点G，连接BC，
∵AB是⊙O的直径，CD⊥AB于D
∴=，
∵=
∴=
∴∠BCF=∠CBF，
∴BF=CF．
【点评】本题考查了等腰三角形的性质，垂径定理，圆周角定理等知识点的应用，解此题的关键是作辅助线后根据定理求出∠CBE=∠BCE，通过做此题培养了学生分析问题和解决问题的能力，题型较好．
　
21．（8分）（2016秋•老河口市期中）如图，要设计一幅长为60cm，宽为40cm的矩形图案，其中有两横两竖的矩形彩条，横竖彩条宽度比为1：2，若彩条所占面积是图案面积的一半，求一条横彩条的宽度．

【分析】设一条横彩条的宽度为xcm，则一条竖彩条的宽度为2xcm．根据“彩条所占面积是图案面积的一半”列出方程并解答即可．
【解答】解：设一条横彩条的宽度为xcm，则一条竖彩条的宽度为2xcm．
根据题意得（60﹣2×2x）（40﹣2x）=，
整理得 x2﹣35x+150=0，
解得x1=5，x2=35，
当x=35时，40﹣2x＜0，不合题意，舍去．
答：一条横彩条的宽度为5cm．
【点评】本题考查的是一元二次方程的应用，设出横、竖条的宽，以面积做为等量关系列方程求解．
　
22．（8分）（2016秋•老河口市期中）如图，AB为⊙O的直径，点C为⊙O上的一点，点D是的中点，过D作⊙O的切线交AC于E，DE=3，CE=1．
（1）求证：DE⊥AC；
（2）求⊙O的半径．

【分析】（1）连接AD，由DE是⊙O的切线，得到∠ODE=90°，根据等腰三角形的性质得到∠ODA=∠OAD，等量代换得到∠CAD=∠ODA，根据平行线的判定 定理得到AE∥OD，于是得到结论；
（2）作OF⊥AC于F，推出四边形OFED是矩形，根据矩形的性质得到OF=ED=3，OD=EF，设⊙O的半径为R，则AF=CF=R﹣1，根据勾股定理列方程即可得到结论．
【解答】（1）证明：连接AD，
∵DE是⊙O的切线，
∴∠ODE=90°，
∵D是的中点，
∴=，
∴∠CAD=∠OAD，
∵OA=OD，
∴∠ODA=∠OAD，
∴∠CAD=∠ODA，
∴AE∥OD，
∴∠AED=180°﹣∠ODE=90°，
∴DE⊥AC；

（2）解：作OF⊥AC于F，
则AF=CF，四边形OFED是矩形，
∴OF=ED=3，OD=EF，
设⊙O的半径为R，则AF=CF=R﹣1，
在Rt△AOF中，AF2+OF2=OA2，
∴（R﹣1）2+32=R2，
解得R=5，
即⊙O的半径为5．

【点评】本题考查了切线的性质，圆心角，弧，弦的关系，正确的作出辅助线是解题的关键．
　
23．（10分）（2016秋•老河口市期中）某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=﹣x+140，该商场销售这种服装获得利润为w元．
（1）求w与x之间的函数关系式；
（2）销售单价定为多少时，商场可获得最大利润？最大利润是多少元？
（3）若该商场想要获得不低于700元的利润，试确定销售单价x的范围．
【分析】（1）根据利润=（售价﹣成本）×销售量列出函数关系式；
（2）直接利用配方法求出二次函数最值即可；
（3）令函数关系式W=700，解得x，然后进行讨论．
【解答】解：（1）根据题意可得：
w=（x﹣60）y，
=（x﹣60）（﹣x+140），
=﹣x2+200x﹣8400，
=﹣（x﹣100）2+1600；

（2）∵w=﹣（x﹣100）2+1600，
a=﹣1＜0，
∴当x=100时，w取最大值，最大值为1600，
∴销售单价定为100元时，商场可获得最大利润，最大利润是1600元；

（3）当w=700时，
﹣（x﹣100）2+1600=700，
解得：x1=70，x2=130，
∵抛物线w=（x﹣100）2+1600开口向下，
∴当70≤x≤130时，w≥750，
∴销售单价x的范围定为：70≤x≤130．
【点评】本题主要考查二次函数的应用，根据利润=（售价﹣成本）×销售量列出函数关系式，求最值，运用二次函数解决实际问题，比较简单．
　
24．（10分）（2016秋•老河口市期中）如图，在等边△ABC中，点D为△ABC内的一点，∠ADB=120°，∠ADC=90°，将△ABD绕点A逆时针旋转60°得△ACE，连接DE．
（1）求证：AD=DE；
（2）求∠DCE的度数；
（3）若BD=1，求AD，CD的长．

【分析】（1）利用旋转的性质和等边三角形的性质先判断出△ADE是等边三角形即可；
（2）利用四边形的内角和即可求出结论；
（3）先求出CD，再用勾股定理即可求出结论．
【解答】（1）证明：∵将△ABD绕点A逆时针旋转60°得△ACE
∴△ABD≌△ACE，∠BAC=∠DAE，
∴AD=AE，BD=CE，∠AEC=∠ADB=120°，
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形，
∴AD=DE，
（2）∠ADC=90°，∠AEC=120°，∠DAE=60°
∴∠DCE=360°﹣∠ADC﹣∠AEC﹣∠DAE=90°，
（3）∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC﹣∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2，
∴AD=DE=2
在Rt△DCE中，．
【点评】此题是旋转的性质，主要考查了等边三角形的性质和判定，勾股定理，解本题的关键是判断出△ADE是等边三角形．
　
25．（12分）（2016秋•老河口市期中）如图，抛物线y=（x﹣1）2+n与x轴交于A，B两点（A在B的左侧），与y轴交于点C（0，﹣3），点D与点C关于抛物线的对称轴对称．
（1）求抛物线的解析式及点D的坐标；
（2）点P是抛物线对称轴上的一动点，当△PAC的周长最小时，求出点P的坐标；
（3）点Q在x轴上，且∠ADQ=∠DAC，请直接写出点Q的坐标．

【分析】（1）利用待定系数法即可求出n，利用对称性C、D关于对称轴对称即可求出点D坐标．
（2）A，P，D三点在同一直线上时△PAC的周长最小，求出直线AD的解析式即可解决问题．
（3）分两种情形①作DQ∥AC交x轴于点Q，此时∠DQA=∠DAC，满足条件．②设线段AD的垂直平分线交AC于E，直线DE与x的交点为Q′，此时∠Q′DA=′CAD，满足条件，分别求解即可．
【解答】解：（1）把C（0，﹣3）代入y=（x﹣1）2+n，得，﹣3=（0﹣1）2+n，
解得n=﹣4，
∴抛物线的解析式为y=（x﹣1）2﹣4，
∴抛物线的对称轴为直线x=1，
∵点D与点C关于抛物线的对称轴对称，
∴点D的坐标为（2，﹣3）．

（2）连接PA、PC、PD

∵点D与点C关于抛物线的对称轴对称
∴PC=PD
∴AC+PA+PC=AC+PA+PD…（5分）
∵AC为定值，PA+PD≥AD
∴当PA+PC的值最小，即A，P，D三点在同一直线上时△PAC的周长最小，
由y=（x﹣1）2﹣4=0解得，x1=﹣1，x2=3，
∵A在B的左侧，∴A（﹣1，0），
由A，D两点坐标可求得直线AD的解析式为y=﹣x﹣1，
当x=1时，y=﹣x﹣1=﹣2，
∴当△PAC的周长最小时，点P的坐标为（1，﹣2），

（3）如图2中，

①作DQ∥AC交x轴于点Q，此时∠DQA=∠DAC，满足条件．
∵A（﹣1，0），C（0，﹣3），
∴直线AC的解析式为y=﹣3x﹣3，
∴直线QD的解析式为y=﹣3x+3，
令y=0得x=1，
∴Q（1，0）．
②设线段AD的垂直平分线交AC于E，直线DE与x的交点为Q′，此时∠Q′DA=′CAD，满足条件，
∵直线AD的解析式为y=﹣x﹣1，
∴线段AD的中垂线是解析式为y=x﹣2，
由解得，
∴E（﹣，﹣），
∴直线DE的解析式为y=﹣x﹣，
令y=0得到x=﹣7，
∴Q′（﹣7，0）．
综上所述，Q点坐标为（1，0）或（﹣7，0）．
【点评】本题考查二次函数综合题、一次函数、最小值问题、等腰三角形的性质、平行线的性质等知识，解题的关键是灵活运用所学知识解决问题，学会利用对称解决最短问题，学会分类讨论的思想思考问题，属于中考压轴题．