

数学九年级上册期末检测卷
展开
这是一份数学九年级上册期末检测卷,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
班级:__________ 姓名:__________ 得分:__________
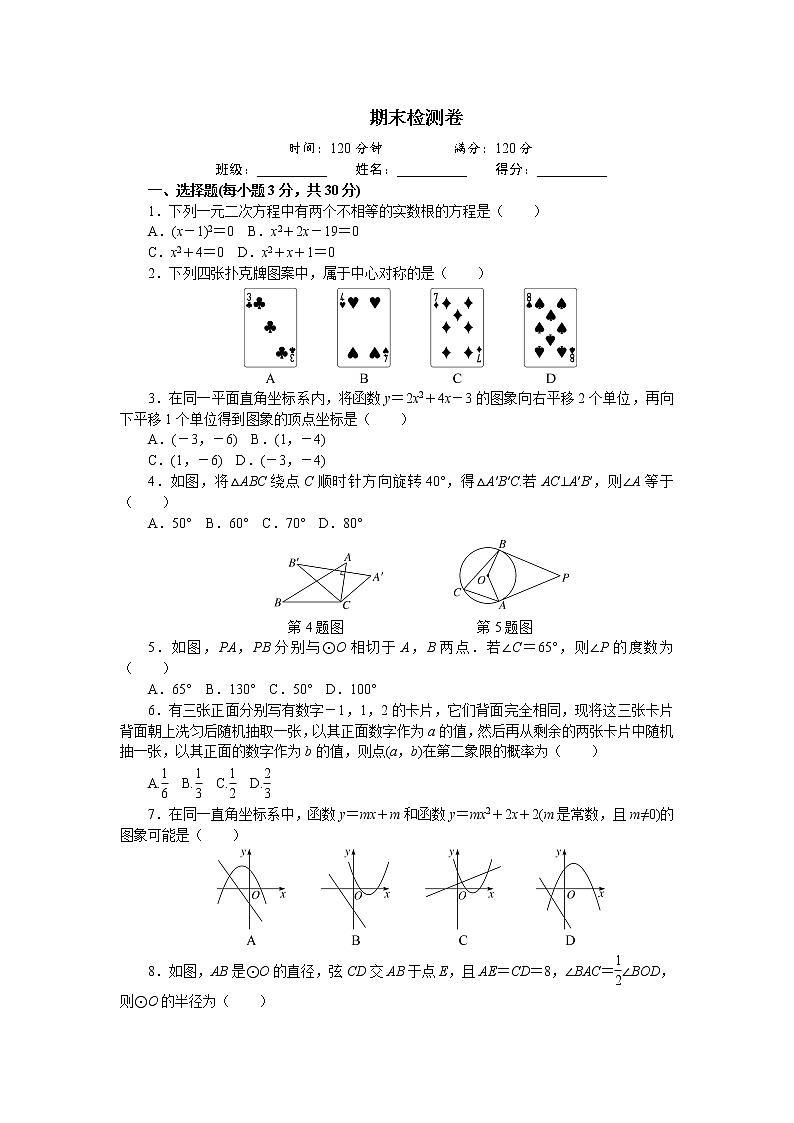
一、选择题(每小题3分,共30分)
1.下列一元二次方程中有两个不相等的实数根的方程是( )
A.(x-1)2=0 B.x2+2x-19=0
C.x2+4=0 D.x2+x+1=0
2.下列四张扑克牌图案中,属于中心对称的是( )
3.在同一平面直角坐标系内,将函数y=2x2+4x-3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )
A.(-3,-6) B.(1,-4)
C.(1,-6) D.(-3,-4)
4.如图,将△ABC绕点C顺时针方向旋转40°,得△A′B′C.若AC⊥A′B′,则∠A等于( )
A.50° B.60° C.70° D.80°
第4题图 第5题图
5.如图,PA,PB分别与⊙O相切于A,B两点.若∠C=65°,则∠P的度数为( )
A.65° B.130° C.50° D.100°
6.有三张正面分别写有数字-1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片中随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为( )
A.eq \f(1,6) B.eq \f(1,3) C.eq \f(1,2) D.eq \f(2,3)
7.在同一直角坐标系中,函数y=mx+m和函数y=mx2+2x+2(m是常数,且m≠0)的图象可能是( )
8.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=eq \f(1,2)∠BOD,则⊙O的半径为( )
A.4eq \r(2) B.5 C.4 D.3
第8题图 第9题图 第10题图
9.如图,在▱ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则▱ABCD的周长为( )
A.4+2eq \r(,2) B.12+6eq \r(,2)
C.2+2eq \r(,2) D.2+eq \r(,2)或12+6eq \r(,2)
10.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(-3,y1)、点Beq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2),y2))、点Ceq \b\lc\(\rc\)(\a\vs4\al\c1(\f(7,2),y3))在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共24分)
11.从1,2,3,4,5,6,7,8,9这九个自然数中,任取一个数是奇数的概率是______.
12.方程2x2-6x-1=0的负数根为___________.
13.抛物线y=4x2-3x与y轴的交点坐标是__________.
14.设m,n分别为一元二次方程x2+2x-2018=0的两个实数根,则m2+3m+n=______.
15.如果点A(-1,4),B(m,4)在抛物线y=a(x-1)2+h上,那么m的值为______.
16.如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:eq \r(,3).将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=_________ .
第16题图 第17题图 第18题图
17.如图,在平行四边形ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F.若弧EF的长为eq \f(π,2),则图中阴影部分的面积为__________.
18.如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是______.
三、解答题(共66分)
19.(8分)用适当的方法解下列方程:
(1)3x(x+3)=2(x+3);
(2)2x2-4x-3=0.
20.(8分)已知抛物线y=-x2+bx+c与直线y=-4x+m相交于第一象限内不同的两点A(5,n),B(3,9),求此抛物线的解析式.
21.(8分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
22.(10分)在⊙O中,AB为直径,C为⊙O上一点.
(1)如图①,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小;
(2)如图②,D为eq \(AC,\s\up8(︵))上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
23.(10分)某中学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是_______事件(填“可能”“必然”或“不可能”);
(2)请用列表或画树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
24.(10分)如图,在四边形ABCD中,AD∥BC,AD=2,AB=2eq \r(,2),以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
(1)求∠ABE的大小及eq \(DEF,\s\up8(︵))的长度;
(2)在BE的延长线上取一点G,使得eq \(DE,\s\up8(︵))上的一个动点P到点G的最短距离为2eq \r(,2)-2,求BG的长.
25.(12分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A,E,N,M为顶点的四边形是平行四边形,且AE为其一边,求点M,N的坐标.
期末检测卷答案
1.B 2.B 3.C 4.A 5.C 6.B 7.D 8.B 9.A
10.B 解析:∵-eq \f(b,2a)=2,∴4a+b=0.故(1)正确;∵x=-3时,y<0,∴9a-3b+c<0,∴9a+c<3b,故(2)错误;由图象可知抛物线经过(-1,0)和(5,0),∴eq \b\lc\{(\a\vs4\al\c1(a-b+c=0,,25a+5b+c=0,))解得eq \b\lc\{(\a\vs4\al\c1(b=-4a,,c=-5a,))∴8a+7b+2c=8a-28a-10a=-30a.∵a<0,∴8a+7b+2c>0,故(3)正确;∵点A(-3,y1)、点Beq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2),y2))、点Ceq \b\lc\(\rc\)(\a\vs4\al\c1(\f(7,2),y3)),eq \f(7,2)-2=eq \f(3,2),2-eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2)))=eq \f(5,2),∴eq \f(3,2)<eq \f(5,2),∴点C离对称轴的距离近,∴y3>y2.∵a<0,-3<-eq \f(1,2)<2,∴y1<y2,∴y1<y2<y3,故(4)错误;∵a<0,∴(x+1)(x-5)=-eq \f(3,a)>0,即(x+1)(x-5)>0,故x<-1或x>5,故(5)正确.∴正确的结论有三个,故选B.
11.eq \f(5,9) 12.x=eq \f(3-\r(11),2) 13.(0,0)
14.2016 15.3 16. 105° 17.2-eq \f(π,2)
18.6 解析:∵A(1,0),B(1-a,0),C(1+a,0)(a>0),∴AB=1-(1-a)=a,CA=a+1-1=a,∴AB=AC.∵∠BPC=90°,∴PA=AB=AC=a.如图,延长AD交⊙D于P′,此时AP′最大.∵A(1,0),D(4,4),∴AD=5,∴AP′=5+1=6,∴a的最大值为6.
19.解:(1)x1=eq \f(2,3),x2=-3;(4分)
(2)x1=1+eq \f(\r(10),2),x2=1-eq \f(\r(10),2).(8分)
20.解:∵直线y=-4x+m过点B(3,9),∴9=-4×3+m,解得m=21,∴直线的解析式为y=-4x+21.(2分)∵点A(5,n)在直线y=-4x+21上,∴n=-4×5+21=1,∴点A(5,1).(4分)将点A(5,1),B(3,9)代入y=-x2+bx+c中,得eq \b\lc\{(\a\vs4\al\c1(1=-25+5b+c,,9=-9+3b+c,))解得eq \b\lc\{(\a\vs4\al\c1(b=4,,c=6,))∴此抛物线的解析式为y=-x2+4x+6.(8分)
21.解:(1)△A1B1C1如图所示;(2分)
(2)△A2B2C2如图所示;(4分)
(3)△PAB如图所示,P(2,0).(8分)
22.解:(1)连接OC,∵⊙O与PC相切于点C,∴OC⊥PC,即∠OCP=90°.(2分)∵OA=OC,∴∠OCA=∠CAB=27°,∴∠COB=2∠CAB=54°.在Rt△COP中,∠P+∠COP=90°,∴∠P=90°-∠COP=36°;(5分)
(2)∵E为AC的中点,∴OD⊥AC,即∠AEO=90°.(6分)在Rt△AOE中,由∠EAO=10°,得∠AOE=90°-∠EAO=80°,∴∠ACD=eq \f(1,2)∠AOD=40°.(8分)∵∠ACD是△ACP的一个外角,∴∠P=∠ACD-∠A=40°-10°=30°.(10分)
23.解:(1)不可能(4分)
(2)画树状图如下:(8分)
共有12种等可能的结果,刚好得到猪肉包和油饼的有2种情况,∴小张同学得到猪肉包和油饼的概率为eq \f(2,12)=eq \f(1,6).(10分)
24.解:(1)连接AE,如图,∵以AD为半径的圆与BC相切于点E,∴AE⊥BC,AE=AD=2.(1分)在Rt△AEB中,AE=2,AB=2eq \r(,2),∴BE=2,即△ABE是等腰直角三角形,∴∠ABE=45°.(3分)∵AD∥BC,∴∠DAB+∠ABE=180°,∴∠DAB=135°,∴eq \(DEF,\s\up8(︵))的长度为eq \f(135π·2,180)=eq \f(3π,2);(5分)
(2)如图,根据两点之间线段最短,可得当A,P,G三点共线时PG最短,(7分)此时AG=AP+PG=2+2eq \r(,2)-2=2eq \r(,2),∴AG=AB.(9分)∵AE⊥BG,∴BE=EG.∴BG=2BE=4.(10分)
25.解:(1)设抛物线解析式为y=a(x-2)2+9,(1分)∵抛物线与y轴交于点A(0,5),∴4a+9=5,∴a=-1,∴y=-(x-2)2+9=-x2+4x+5;(3分)
(2)当y=0时,-x2+4x+5=0,∴x1=-1,x2=5,∴E(-1,0),B(5,0).(4分)设直线AB的解析式为y=mx+n,∵A(0,5),B(5,0),∴m=-1,n=5,∴直线AB的解析式为y=-x+5.设P(x,-x2+4x+5),∴D(x,-x+5),∴PD=-x2+4x+5+x-5=-x2+5x.(5分)∵AC∥x轴,∴点A,C关于对称轴对称,AC=4.∵AC⊥PD,∴S四边形APCD=eq \f(1,2)×AC×PD=2(-x2+5x)=-2x2+10x,∴当x=-eq \f(10,2×(-2))=eq \f(5,2)时,即点P的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2),\f(35,4)))时,S四边形APCD最大=eq \f(25,2);(7分)
(3)如图,过M作MH垂直于对称轴,垂足为H.∵MN∥AE,MN=AE,∴△HMN≌△OEA,∴HM=OE=1,∴M点的横坐标为3或1.当横坐标1时,M点纵坐标为8,当横坐标为3时,M点纵坐标为8,∴M点的坐标为M1(1,8)或M2(3,8).(9分)∵A(0,5),E(-1,0),∴直线AE的解析式为y=5x+5.∵MN∥AE,∴MN的解析式为y=5x+b.∵点N在抛物线对称轴x=2上,∴N(2,10+b).∵AE2=OA2+OE2=26=MN2,∴MN2=(2-1)2+[8-(10+b)]2=1+(b+2)2.∵M点的坐标为M1(1,8)或M2(3,8),∴点M1,M2关于抛物线对称轴x=2对称.∵点N在抛物线对称轴上,∴M1N=M2N.∴1+(b+2)2=26,∴b=3或b=-7,∴10+b=13或10+b=3.∴当M点的坐标为(1,8)时,N点坐标为(2,13),当M点的坐标为(3,8)时,N点坐标为(2,3).(12分)
相关试卷
这是一份【期末仿真检测】沪教版数学 九年级上册一模(期末)检测卷(满分卷),文件包含期末仿真检测沪教版数学九年级一模期末检测卷满分卷解析版docx、期末仿真检测沪教版数学九年级一模期末检测卷满分卷原卷版docx等2份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。
这是一份【期末仿真检测】沪教版数学 九年级上册一模(期末)检测卷(学霸卷),文件包含期末仿真检测沪教版数学九年级一模期末检测卷学霸卷解析版docx、期末仿真检测沪教版数学九年级一模期末检测卷学霸卷原卷版docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
这是一份【期末仿真检测】沪教版数学 九年级上册一模(期末)检测卷(冲刺卷),文件包含期末仿真检测沪教版数学九年级一模期末检测卷冲刺卷解析版docx、期末仿真检测沪教版数学九年级一模期末检测卷冲刺卷原卷版docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。









