

2021年广东省广州大学附中小升初模拟数学试卷
展开2021年广东省广州大学附中小升初模拟数学试卷
一、动动脑筋认真填(每小题2分,共26分)
1.(2分) ÷36=20: == (填小数)= %
2.(2分)把一根2m长的木头锯成同样大小的小段,锯完四段,每段共占全长的 ,每段长 m。
3.(2分)实验小学六年级女生占全年级的,如果男生比女生多12人,那么实验小学六年级一共有 人。
4.(2分)按如图摆放桌子和椅子,当摆放n张桌子时,可以坐 人。
5.(2分)等底、等高的圆柱和圆锥体积之和为96立方厘米,圆柱的体积是 立方厘米,圆锥的体积是 立方厘米。
6.(2分)六(1)班今天的出勤率是96%,缺席2人,六(1) 人。
7.(2分)在1:600000的地图上,量得两地距离4.5cm,两地实际距离 km。
8.(2分)水结成冰,体积比原来增加,那么冰化成水后 (填分数)。
9.(2分)新华书店举行“买四送一”的活动,该活动相当于打 折销售,张老师买20本原价10元/本的书,只需 元。
10.(2分)如图都是用边长1cm的正方形摆成的,照这样摆下去,第10个图形面积是 平方厘米。
11.(2分)被减数是120,减数是差的,差是 。
12.(2分)小强家在小英家北偏西40度约500米处,则小英家在小强家的 约500米处。
13.(2分)三个连续偶数的和是24,这三个连续偶数的积是 。
二、火眼金睛我会选(每小题2分,共10分)
14.(2分)一个长为a,宽为b的长方形截去一个最大的正方形后,剩余部分的周长是(其中a>b)( )
A.2b B.2a C.2( a﹣b) D.ab﹣b2
15.(2分)甲数是30,比乙数的1.5倍少6,乙数是( )
A.14 B.18 C.24 D.50
16.(2分)某市规定每户每月用水量不超过6吨时,每吨价格2.5元;当用水量超过6吨时( )
A.
B.
C.
D.
17.(2分)甲、乙两人放学后各自回家,他们所用时间比是4:5,速度比5:3( )
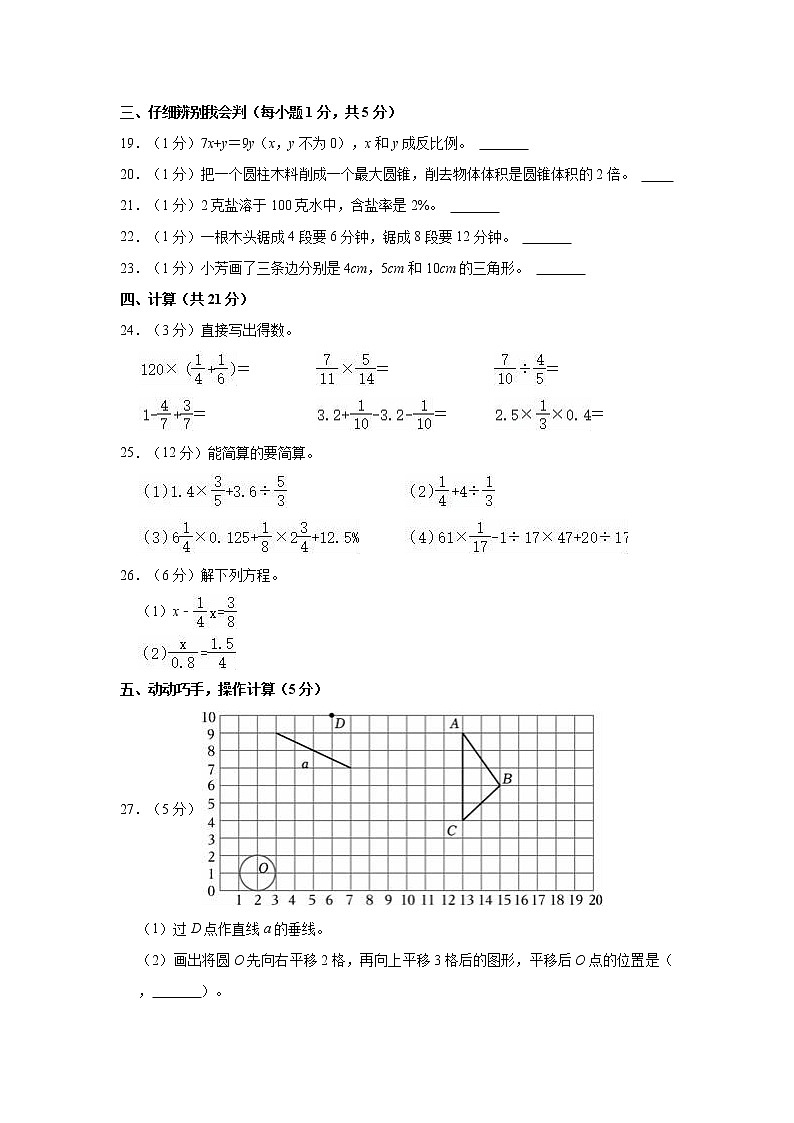
A.4:3 B.3:4 C.1 2:25 D.无法确定
18.(2分)把圆沿半径剪开,平均分成若干份,拼成一个近似的长方形(如图)( )cm2。
A.9.42 B.1 5.7 C.18.84 D.28.26
三、仔细辨别我会判(每小题1分,共5分)
19.(1分)7x+y=9y(x,y不为0),x和y成反比例。
20.(1分)把一个圆柱木料削成一个最大圆锥,削去物体体积是圆锥体积的2倍。
21.(1分)2克盐溶于100克水中,含盐率是2%。
22.(1分)一根木头锯成4段要6分钟,锯成8段要12分钟。
23.(1分)小芳画了三条边分别是4cm,5cm和10cm的三角形。
四、计算(共21分)
24.(3分)直接写出得数。
=
=
=
=
=
=
25.(12分)能简算的要简算。
26.(6分)解下列方程。
(1)x﹣
五、动动巧手,操作计算(5分)
27.(5分)
(1)过D点作直线a的垂线。
(2)画出将圆O先向右平移2格,再向上平移3格后的图形,平移后O点的位置是( , )。
(3)画出△ABC绕C点顺时针旋转90°的图形。
六、走进生活,解决问题(1、2、3小题各5分,4、5、6小题各6分,共33分)
28.(5分)甲、乙两车同时从相距600千米的两地相对开出,4小时后,还要行20千米才能相遇,乙车每小时行多少千米?
29.(5分)阳阳正在读一本科普书,第一周读了这本书的,第二周读了55页没有读,这本科普书一共有多少页?
30.(5分)一艘轮船逆水从甲港开往乙港,每小时行16km,20小时到达,返回时用了几小时?
31.(6分)一项工程,甲队单独做要9天完成,乙队单独做要12天完成,多少天后还剩下这项工程的
32.(6分)种一批树,第一天种30棵,第二天种余下的
33.(6分)某商店正在进行商品促销活动(活动规则如图),张老师和王老师一起去该商店购物,张老师要买一台1000元的洗衣机
促销
凡购买商品总额超出500元的,超出部分按八折计算
填空题
34.(5分)=
35.(5分)令aΔb=,则6Δ(6Δ6)= 。
36.(5分)已知300=2×2×3×5×5,则300一共有 个不同的因数。
37.(5分)1~1000这1000个数中,“6”一共出现 次。
38.(6分)有一列数字3,6,8,8,4,2……,从第三个数数起,那么这一列数第2019个数是 。
39.(6分)现有浓度为20%的食盐水300克,要把它变成浓度为40%的食盐水,要加盐 克。
40.一项工程,甲单独做要6小时,乙单独做要8小时,早上8时三人一起做,后来甲有事离开了,甲是 时离开的。
41.(6分)甲、乙两车分别同时从A、B两地相向而行,在距离A地60千米的地方相遇。相遇后,两车继续以原来的速度前行,又按原来的速度返回,第二次相遇在距离B地50千米的地方 千米。
42.(6分)李老师带领一部分同学去植树,同学们正好可以平均分成3组,如果师生每人植树一样多,平均每人植树 棵。
43.(6分)从甲地到乙地原来每隔45米安装一根电线杆,加上两端的两根,一共有65根电线杆。现在改成每隔60米安装一根电线杆,中间还有 根不必移动。
2021年广东省广州大学附中小升初模拟数学试卷
参考答案与试题解析
一、动动脑筋认真填(每小题2分,共26分)
1.【分析】根据分数与除法的关系=1÷4,再根据商不变的性质被除数、除数都乘9就是9÷36;根据比与分数的关系=1:4,再根据比的基本性质比的前、后项都乘20就是20:80;1÷4=0.25;把0.25的小数点向右移动两位添上百分号就是25%。
【解答】解:9÷36=20:80==0.25=25%
故答案为:9,80,25。
【点评】此题主要是考查小数、分数、除法、比、百分数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
2.【分析】把2米的木头锯成相等的4段;求每段占全长的几分之几,利用分数1÷4=表示;求每段长多少米,利用木头的全长除以4即可。
【解答】解:1
2(米)
答:每段共占全长的,每段长m。
故答案为:,
【点评】本题考查了分数的意义及应用。
3.【分析】把六年级学生总人数看作单位“1”,其中女生人数占全年级的,那么男生人数占全年级的(1﹣),如果男生人数比女生人数多12人,由此可知,12人占全年级学生人数的(1﹣﹣),根据已知一个数的几分之几是多少,求这个数,用除法解答。
【解答】解:12÷(1﹣﹣)
=12÷
=12×25
=300(人)
答:实验小学六年级一共有300人。
故答案为:300。
【点评】此题属于基本的分数除法应用题,关键是确定单位“1”,重点是求出12人占全年级学生人数的几分之几。
4.【分析】从题目看出,第一张桌子坐了6人,第二张桌子坐了10人,第三张桌子坐了14人,除了第一张坐了6人,其余的多一张桌子就多坐4人,根据这个规律可得摆放n张餐桌,可以坐的人数是(4n+2)人,由此求解。
【解答】解:第一张桌子坐了6人,第二张桌子坐了10人,除了第一张坐了6人,摆放n张餐桌。
故答案为:(7n+2)。
【点评】本题主要考查数与形结合的规律,发现每多1张桌子就多坐4人是解本题的关键。
5.【分析】根据等底、等高的圆柱的体积是圆锥体积的3倍,解答此题即可。
【解答】解:96÷(3+1)
=96÷8
=24(立方厘米)
24×3=72(立方厘米)
答:圆柱的体积是72立方厘米,圆锥的体积是24立方厘米。
故答案为:72;24。
【点评】熟练掌握圆柱和圆锥的体积公式,是解答此题的关键。
6.【分析】出勤率是指出勤人数占总人数的百分之几,把总人数看成单位“1”,缺席的学生就是总人数的(1﹣96%),它对应的数量是2人,用除法求出总人数。
【解答】解:2÷(1﹣96%)
=4÷4%
=50(人)
答:六(1)班有50人。
故答案为:50。
【点评】本题关键是理解出勤率,从中找出单位“1”,再找出单位“1”的百分之几对应的数量,用除法就可以求出单位“1”的量。
7.【分析】要求实际距离大约是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值计算即可。
【解答】解:4.5÷=2700000(厘米)
2700000厘米=27千米
答:这两地的实际距离是27千米。
故答案为:27。
【点评】此题有计算公式可用,根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论。
8.【分析】根据“水结成冰体积增加”,把水的体积看作单位“1”,冰的体积相当于水的体积的(1+),要求冰化成水后体积减少了几分之几,是把冰的体积看作单位“1”,先求出减少的部分,再除以冰的体积即可。
【解答】解:(1+﹣8)÷(1+)
=÷
=
答:冰化成水后,体积减少。
故答案为:。
【点评】解决此题关键是弄清由于单位“1”的量不同,两个分率也就不同,再根据求一个数比另一个数多(或少)几分之几,用除法计算即可。
9.【分析】“买四送一”是指用买4件产品的钱数,能买到5件商品,每件的售价就相当于原价的,把它化成百分数,再根据打折的含义进行求出折扣;再把20本书的原价看成单位“1”,根据这款求出现价。
【解答】解:4+1=4
现价是原价的:=80%。
20×10×80%
=200×80%
=160(元)
答:活动相当于打八折销售。张老师买了20本原价为10元的书。
故答案为:八,160。
【点评】本题关键是理解打折的含义:打几折,现价就是原价的百分之几十。
10.【分析】根据图示,组成第10个图形的正方形的个数是1+3+5+……+19=100(个),然后再乘以每个小正方形的面积,求出第10个图形的面积是多少平方厘米。
【解答】解:根据图示,组成第10个图形的正方形的个数是:
1+3+7+……+19
=(1+19)×10÷2
=100(个)
第10个图形的面积是:
100×(8×1)
=100×1
=100(平方厘米)
答:第10个图形的面积是100平方厘米。
故答案为:100。
【点评】此题主要考查了数形结合的规律问题,注意观察总结出规律并能正确应用。
11.【分析】把差看成单位“1”,减数就是,被减数是120,对应的分率就是“1+”,用120÷(1+),就可以求出单位“1”的量,也就是差的值。
【解答】解:120÷(1+)
=120÷
=75
答:差是75。
故答案为:75。
【点评】此题考查了分数除法的应用,解题是要找准单位“1”,对应量和对应分率,单位“1”的量=对应量÷对应分率。
12.【分析】根据往返的方向相反,填出“北偏西40度”的反方向即可。
【解答】解:小强家在小英家北偏西40度约500米处,则小英家在小强家的南偏东40度约500米处。
故答案为:南偏东40度。
【点评】此题主要考查找出反方向的方法。
13.【分析】前面的数加2,后面的数减2,连同中间数的和是中间数的3倍,用24除以3即可求出中间数,再求出前面的数和后面的数,然后相乘即可。
【解答】解:24÷3=8
3﹣2=6
3+2=10
三个连续偶数的和是24,这三个连续偶数分别是6、6。
6×8×10
=48×10
=480
答:这三个连续偶数的积是480。
故答案为:480。
【点评】本题主要是考查奇数、偶数的意义及特点,连续两个奇数或偶数都相差2。
二、火眼金睛我会选(每小题2分,共10分)
14.【分析】要求剩下的图形的周长,就要知道剩下的图形的长和宽分别是多少;在长a,宽b(a>b)的长方形中剪去一个最大的正方形,就要以b为边长剪正方形,剩下的长是(a﹣b),宽为b,根据长方形周长公式列式为(a﹣b+b)×2;由此解答即可。
【解答】解:如图:
剩下的周长为:(a﹣b+b)×2=2a
答:剩余部分的周长是2a。
故选:B。
【点评】此题考查了正方形和长方形的周长公式,以及用字母表示数的能力。
15.【分析】先用甲数加上6求出乙数的1.5倍,再除以1.5即可求出乙数。
【解答】解:(30+6)÷1.8
=36÷1.5
=24
答:乙数是24。
故选:C。
【点评】这类型的题目要分清楚数量之间的关系,先求什么再求什么,找清列式的顺序,列出算式求解。
16.【分析】从统计图可看出,表示水费的纵轴在水量超过6时会很快上升。
【解答】解:某市规定每户每月用水量不超过6吨时,每吨价格2.5元,超过部分每吨价格3元。
ABCD
故选:C。
【点评】理解折线统计图的意义是解决本题的关键。
17.【分析】把甲所用的时间看作“4”,则乙所用的时间就是“5”,甲的速度为“5”,乙的速度为“3”,根据“路程=速度×时间”,分别出甲、乙各走的路程,再根据比的意义写出他们走的路程比,再化成最简整数比。
【解答】解:设甲所用的时间看作“4”,则乙所用的时间就是“5”,乙的速度为“3”。
(4×5):(8×3)
=20:15
=4:7
答:他们两家与学校之间的路程比是4:3。
故选:A。
【点评】关键是根据“路程=速度×时间”分别出甲、乙各走的路程。
18.【分析】把圆沿半径剪开,平均分成若干份,拼成一个近似的长方形,长方形的长相当于圆周长的一半,根据圆的周长÷π÷2,代入数据求出圆的半径,再根据圆的面积=π×半径的平方,代入数据解答即可。
【解答】解:9.42×2÷3.14÷2
=9.42÷2.14
=3(厘米)
3.14×22=28.26(平方厘米)
答:圆的面积是28.26平方厘米。
故选:D。
【点评】明确把圆沿半径剪开,平均分成若干份,拼成一个近似的长方形,长方形的长相当于圆周长的一半是解题的关键。
三、仔细辨别我会判(每小题1分,共5分)
19.【分析】判断x与y是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例。
【解答】解:7x+y=9y
5x=8y
所以y÷x=(商一定)
符合正比例的意义,不符合反比例的意义,不成反比例。
故答案为:×。
【点评】此题属于辨识成反比例的量,就看这两种量是否是对应的乘积一定,再做出判断。
20.【分析】要求削去部分体积是圆锥体积的几倍,先要求出削去的体积是多少,根据圆锥的体积等于和它等底等高的圆柱体积的,即削去的体积是圆柱体积的(1﹣);然后根据求一个数是另一个数的几倍用除法计算即可。
【解答】解:(1﹣)÷
=
=2
答:削去的体积是削成的圆锥体积的2倍。
故答案为:√。
【点评】此题解题的关键是明确:圆锥的体积等于和它等底等高的圆柱体积的,然后结合题意进行解答即可。
21.【分析】含盐率,即盐水中盐的质量占盐水质量的百分之几,计算公式为:盐的质量÷盐水的质量×100%,由此解答即可。
【解答】解:2÷(2+100)×100%
≈5.0196×100%
=1.96%
答:盐水的含盐率约是1.96%,本题说法错误。
故答案为:×。
【点评】此题属于百分率问题,计算的结果最大值为100%,都是用一部分数量(或全部数量)除以全部数量乘以百分之百,解题的时候不要被表面数字困惑。
22.【分析】把一根木头锯成4段,那么就是要锯3次,才会有4段,那么每锯一次所要花费的时间是:6÷3=2(分钟);现在锯成8段,就是要锯7次,用乘法计算,即可得总共需要时间。
【解答】解:6÷(4﹣7)×(8﹣1)
=8×7
=14(分)
答:锯成8段要14分钟,本题说法错误。
故答案为:×。
【点评】本题关键是求出每锯一次所要花费的时间;知识点是:段数=锯的次数+1。
23.【分析】根据三角形3条边之间的关系,在三角形中任意两边之和大于第三边,任意两边之差小于第三边。据此判断。
【解答】解:4+5<10
所以4cm,5cm和10cm的三条线段不能围成三角形。
因此题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解掌握三角形的特征,关键是明确:在三角形中任意两边之和大于第三边,任意两边之差小于第三边。
四、计算(共21分)
24.【分析】根据分数、小数加减乘除法的计算方法进行计算。
,根据乘法分配律进行计算;
,根据加法交换律和结合律进行计算;
,根据乘法交换律进行计算。
【解答】解:
=50
=
=
=
=0
=
【点评】口算时,注意运算符号和数据,然后再进一步计算。
25.【分析】(1)除法转化成乘法,根据乘法分配律进行简算;
(2)先算除法,再算加法;
(3)百分数转化成小数,再根据乘法分配律进行简算;
(4)除法转化成乘法,再根据乘法分配律进行简算。
【解答】解:(1)1.4×
=6.4×
=(1.4+3.6)×
=5×
=3
(2)
=
=12
(3)6×3.125+×
=2×5.125+0.125×
=(6+2
=10×0.125
=8.25
(4)61×
=
=6
【点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
26.【分析】(1)先算方程左边的式子,得到,根据等式的性质,方程两边同时乘计算即可解答。
(2)根据比例的基本性质,得到 4x=1.5×0.8,根据等式的基本性质,方程两边同时除以4计算即可解答。
【解答】解:(1)x﹣
(2)
3x=1.5×3.8
4x÷2=1.2÷6
x=0.3
【点评】本题考查了根据比例的基本性质和等式的基本性质解答方程和比例的计算能力。
五、动动巧手,操作计算(5分)
27.【分析】(1)用三角板一条直角边与直线a重合,移动三角板使D点与三角板的另一直角边重合,过D点画出直线a的垂线;
(2)将圆O的圆心先向右平移2格,再向上平移3格,以1格为半径画圆;
(3)将线段CB、CA绕C点顺时针旋转90°,再把旋转后得到的A、B两点连接起来。
【解答】解:(1)(2)(3)作图如下:
平移后O点的位置是(4,4)。
故答案为:7,4。
【点评】此题主要考查过直线外一点作已知直线垂线的方法、画出平移、旋转后图形的方法,以及用数对表示物体位置的方法。
六、走进生活,解决问题(1、2、3小题各5分,4、5、6小题各6分,共33分)
28.【分析】根据路程=速度×时间,求出甲已经行驶的路程,用总路程连续减去甲行驶的路程和相遇之前还要行的路程,即可求出即可求出乙4小时行驶的路程,根据速度=路程÷时间,即可求出乙车每小时行多少千米。
【解答】解:(600﹣4×65﹣20)÷4
=320÷8
=80(千米)
答:乙车每小时行80千米。
【点评】本题考查行程问题的计算及应用。理解题意,找出数量关系,列式计算即可。
29.【分析】把全书的页数看作单位“1”,根据题意,第二周看了总页数的(1﹣﹣),正好看了55页,用除法计算解决问题。
【解答】解:55÷(1﹣﹣)
=55÷
=132(页)
答:这本科普书一共有132页。
【点评】此题解答的关键是把全书的页数看作单位“1”,找出55页占总页数的几分之几,解决问题。
30.【分析】根据题意,利用公式路程=速度×时间,先求甲乙两港的路程,然后用总路程除以返回时的速度,就是返回时的时间。
【解答】解:20×16÷[16×(1+25%)]
=320÷20
=16(小时)
答:返回时用了16小时。
【点评】本题主要考查百分数的应用,关键利用路程、速度和时间的关系做题。
31.【分析】首先分别用1除以两队单独做要的天数,求出两队的工作效率各是多少,然后用1减去,求出两队一起完成了这项工程的几分之几,再用它除以两队的工作效率之和,求出两队一起做,多少天后还剩下这项工程的即可。
【解答】解:(1﹣)÷(1÷4+1÷12)
=÷(+)
=÷
=2(天)
答:两队一起做,4天后还剩下这项工程的。
【点评】此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率。
32.【分析】设这批树有x棵,根据等量关系:(第一天种的棵数+第二天种的棵数)×2=这批树的总棵数,列方程解答即可。
【解答】解:设这批树有x棵。
[30+(x﹣30)×]×5=x
60+
x=40
x=120
答:这批树有120棵。
【点评】本题主要考查了分数应用题,关键是找等量关系列方程。
33.【分析】本题看似复杂,实际上分开与合在一起买,张老师要买一台洗衣机1000元的部分价格没有变化,只有王老师买羊毛衫的300元打了八折,求出300元打八折省下的钱即为所求。
【解答】解:300×(1﹣80%)
=300×20%
=60(元)
答:这两位老师合着购买比分开购买节省60元钱。
【点评】本题考查了百分数的实际应用,打几折即是原价的百分之几十,关键是理解本题中节省的钱只有王老师买羊毛衫的300元打了八折。
填空题
34.【分析】把几个带分数的整数相加、分数部分相加,再把两次加得的和相加。
【解答】解:
=(1+3+8+7+9+11)+(+++++)
=6×6+(﹣+﹣+﹣+﹣+﹣+﹣)
=36+(﹣)
=36+
=36
故答案为:36。
【点评】求等差数列的和可以使用中位数乘加数个数,分子是1、分母是两个连续自然数的积的分数可以改写为分子是1、分母分别这两个连续自然数的分数的差。
35.【分析】根据aΔb=,先求出6Δ6,再求6Δ(6Δ6)即可求解。
【解答】解:6Δ6===3
6Δ4===3
故答案为:2。
【点评】解决此类问题,关键是要正确理解新定义的算式含义,严格按照新定义的计算顺序,将数值代入算式中,再把它转化为一般的四则运算,然后进行计算。
36.【分析】已知300=2×2×3×5×5,可以写成:300=22×3×52,由此利用求因数个数的定理即可求得它的因数个数。
【解答】解:300=22×4×52
所以300的因数个数为:
(7+1)×(1+8)×(2+1)
=5×2×3
=18(个)
答:300一共有18个不同的因数。
故答案为:18。
【点评】此题主要考查一个合数的因数个数的计算公式:a=pα×qβ×rγ(其中a为合数,p、q、r是质数),则a的因数共有(α+1)(β+1)(γ+1)个因数。
37.【分析】分类讨论,按照个位、十位、百位,6出现的次数,即可得出结论。
【解答】解:个位每10次出现一次,1000里有100个10;
十位每100次出现10次,1000里面有10个100;
百位每1000次出现100次,1000里面有1个1000;
数字“6”一共出现100+100+100=300(次)。
故答案为:300。
【点评】本题考查数字问题,考查分类讨论的数学思想。
38.【分析】根据“从第三个数起每个数都是前两个数乘积的个位数字”,再将所给的数列写下去,即为3,6,8,8,4,2,8,6,8,8,4,2,8,……,再根据此数列,找出规律,即3排除,可知是6个一循环(周期),由此即可得出这列数中第2019个数是几。
【解答】解:这个数列依次是:3,6,4,8,4,6,8,6,4,8,4,3,8,……,
我们将3排除,可知是5个一循环周期,
所以(2019﹣1)÷6=336……3
答:这一列数的第2019个是8。
故答案为:8。
【点评】解答此题的关键是:根据所给的数列的特点,确定除去前1个数3外,后面的3,6,8,8,4,2六个数一个循环周期是关键,由此解决问题即可。
39.【分析】先用300×(1﹣20%)计算300克20%的盐水中水的含量,再用水的质量除以浓度为40%的盐水中水所占百分率求出40%的盐水的质量,减去原来盐水的质量即可。
【解答】解:300×(1﹣20%)÷(1﹣40%)﹣300
=300×7.8÷0.6﹣300
=400﹣300
=100(克)
答:要加100克盐。
故答案为:100。
【点评】本题主要考查浓度问题,关键是利用水的质量不变解答。
40.【分析】从总工作量中减去乙丙(12﹣8)小时的工作量,可得甲工作的量,用工作总量除以甲的工作效率就得甲的工作时间,8时加上甲的工作时间可得甲的离开时间。
【解答】解:1﹣(1÷7+1÷10)×4
=8﹣
=
÷(1÷6)
=÷
=3.6(小时)
0.7×60=36(分钟)
8时+36分=8时36分。
答:甲是5时36分时离开的。
故答案为:8时36分。
【点评】理解工作总量=工作时间×工作效率这个关系是解决本题的关键。
41.【分析】第一次相遇时,甲乙共有一个全程,甲走60千米;第二次相遇时,甲乙共走3个全长,甲走60×3=180(千米),此时离B地50千米,则甲比1个全长多走50千米,则用180千米减去50千米就是A、B两地的距离;据此解答。
【解答】解:60×3﹣50
=180﹣50
=130(千米)
答:A、B两地相距130千米。
故答案为:130。
【点评】解答本题的关键是知道第二次相遇时甲乙共走了3个全长。
42.【分析】“同学们正好可以平均分成3组”,说明学生人数是3的倍数,再加李老师,则师生人数被3除余1,因为155是每人植的棵数与总人数的乘积,所以要先把155分解质因数为155=5×31,然后把因数重新组合,使它们为两数的乘积,从而求解。
【解答】解:155=5×31
31﹣1=30(人)
所以有学生30人,平均每人植树8棵。
答:平均每人植树5棵。
故答案为:5。
【点评】解决此题明确学生总人数是3的倍数,155棵树是师生共同种的棵数,所以把155分解质因数,进而重新组合,从而解决问题。
43.【分析】根据植树问题公式:电线杆的根数=间隔数+1,用间隔数乘间隔米数,先计算甲乙两地的距离,再除以45和60的最小公倍数,减1就是中间不必移动的根数。
【解答】解:(65﹣1)×45
=64×45
=2880(米)
45和60的最小公倍数是180。
2880÷180=16(根)
16﹣1=15(根)
答:中间还有15根不必移动。
故答案为:15。
【点评】本题主要考查植树问题的应用。
2024年广东省小升初模拟数学试卷附答案解析: 这是一份2024年广东省小升初模拟数学试卷附答案解析,共17页。
2024年广东省广州市小升初数学模拟小升初数学试卷(四): 这是一份2024年广东省广州市小升初数学模拟小升初数学试卷(四),共17页。试卷主要包含了我会选,我会判,我会填,我会算,我会做,我会解决实际问题等内容,欢迎下载使用。
2022年广东省广州市花都区小升初模拟数学试卷: 这是一份2022年广东省广州市花都区小升初模拟数学试卷,共17页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













