2023届内蒙古呼和浩特市第二中学高三下学期2月份测试（一模考前模拟）数学（文）试题含解析

这是一份2023届内蒙古呼和浩特市第二中学高三下学期2月份测试（一模考前模拟）数学（文）试题含解析，共18页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
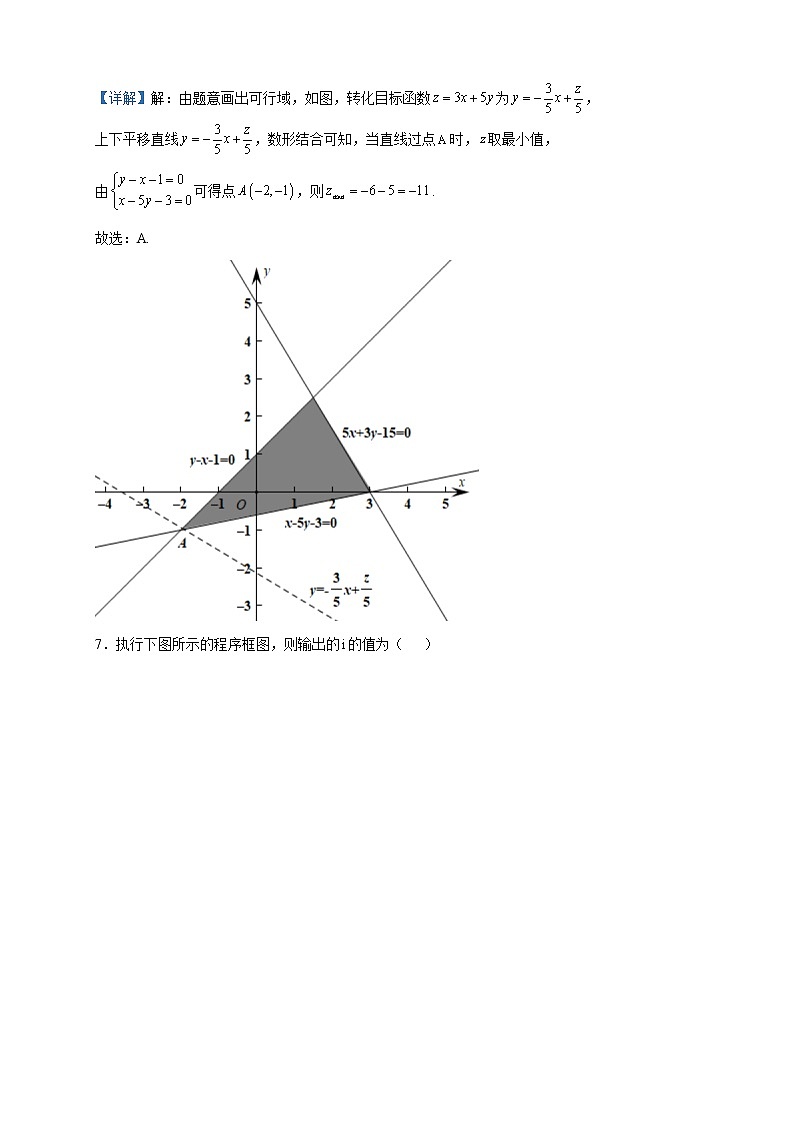
2023届内蒙古呼和浩特市第二中学高三下学期2月份测试（一模考前模拟）数学（文）试题 一、单选题1．设全集，，则为（    ）A． B． C． D．【答案】A【分析】根据全集求出的补集即可.【详解】，，.故选：A.2．复数，则（    ）A．10 B． C． D．【答案】D【分析】由,可知共轭复数，代入后化简即可求解.【详解】由,可知共轭复数，.故选：D.3．总体由编号01，,02，…，19,20的20个个体组成．利用下面的随机数表选取5个个体，选取方法是随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为7816657208026314070243699728019832049234493582003623486969387481 A．08 B．07 C．02 D．01【答案】D【详解】从第一行的第5列和第6列起由左向右读数划去大于20的数分别为：08,02,14,07,01，所以第5个个体是01，选D.【解析】此题主要考查抽样方法的概念、抽样方法中随机数表法，考查学习能力和运用能力.4．已知，则的值为（    ）A． B． C． D．【答案】A【分析】根据给定条件，利用诱导公式和二倍角的余弦公式计算作答.【详解】因，所以.故选：A5．已知为等比数列，是它的前项和，若，且与的等差中项为，则等于（    ）A．35 B． C． D．【答案】C【分析】根据等差中项的性质得到，结合，利用等比数列的基本量求得和公比，再由等比数列的求和公式即可得到.【详解】因为与的等差中项为，所以，设等比数列的公比为（），又，得：，解得：，则，故选：C.6．若x，y满足约束条件，则的最小值为（    ）A． B．17 C．11 D．【答案】A【分析】由题意画出可行域，转化目标函数为，数形结合即可得解.【详解】解：由题意画出可行域，如图，转化目标函数为，上下平移直线，数形结合可知，当直线过点时，取最小值，由可得点，则.故选：A.7．执行下图所示的程序框图，则输出的的值为（     ） A．5 B．6 C．4 D．3【答案】A【解析】执行如图所示程序框图，逐一进行运算，即可求出结果.【详解】依次执行如下：，；，；，；，，满足条件，退出循环体，输出，故选：A.【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．8．过点作圆的两条切线，切点分别为，则弦长（    ）A． B． C． D．【答案】A【分析】结合直线与圆的位置关系，解三角形即可得结果.【详解】∵分别为圆的切线，∴∵，，∴，又∵，在中，，∴，∴.故选：A9．若，则向量与的夹角为（    ）A． B． C． D．【答案】B【分析】由得及可求解.【详解】由，有，两边平方有，化简得，所以，所以向量与的夹角为.故选：B10．已知抛物线：的焦点为,是C上一点，，则（  ）A．1 B．2 C．4 D．8【答案】A【分析】解方程即得解.【详解】解：由题得抛物线的准线方程为，则有，即有，解得．故选：A11．“阿基米德多面体”也称半正多面体，是由边数不全相同的正多边形围成的多面体，它体现了数学的对称美.如图是以一正方体的各条棱的中点为顶点的多面体，这是一个有八个面为正三角形，六个面为正方形的“阿基米德多面体”，若该多面体的棱长为1，则经过该多面体的各个顶点的球的体积为（    ）A． B． C． D．【答案】A【分析】将该多面体放入正方体中，可以间接确定该多面体外接球的球心，从而求出其外接球的体积【详解】将该多面体放入正方体中, 如图所示.由于多面体的棱长为, 所以正方体的棱长为 因为该多面体是由棱长为的正方体连接各棱中点所得,所以该多面体外接球的球心为正方体体对角线的中点，其外接球直径等于正方体的面对角线长，即所以所以该多面体外接球的体积 . 故选：A.12．已知是定义域为R的函数，且函数的图象关于直线对称，当时，，设，，，则a，b，c的大小关系为（　　）A． B． C． D．【答案】B【分析】由函数性质判断函数的对称性与单调性，构造函数即可比较与大小，又因为，即可求出结果．【详解】由于函数的图象关于直线对称，所以的图象关于直线对称，因为在上单调递减，所以在上单调递减，构造函数，则当时，，所以在上单调递减，故，所以，故又因为，所以故故选：B 二、填空题13．当时，的最小值为______．【答案】5【分析】将所求代数式变形为，利用基本不等式即可求解.【详解】解：因为，所以，所以，当且仅当，即时等号成立，所以的最小值为.故答案为：.14．已知的内角A，B，C的对边分别为a，b，c，已知，，且，则___________.【答案】【分析】由题意和正弦定理得到，结合余弦定理化简得到，即可求解.【详解】因为，由正弦定理，可得，又因为，所以，解得，由余弦定理知，所以，即，解得.故答案为：.15．2022年北京冬奥会开幕式始于24节气倒计时，它将中国人的物候文明、传承久远的诗歌、现代生活的画面和谐统一起来.我国古人将一年分为24个节气，如图所示，相邻两个节气的日晷长变化量相同，冬至日晷长最长，夏至日晷长最短，周而复始.已知冬至日晷长为13.5尺，芒种日晷长为2.5尺，则一年中夏至到大雪的日晷长的和为______尺.【答案】84【分析】根据给定条件可得以冬至日晷长为首项，芒种日晷长为第12项的等差数列，求出公差即可列式计算作答.【详解】依题意，冬至日晷长为13.5尺，记为，芒种日晷长为2.5尺，记为，因相邻两个节气的日晷长变化量相同，则从冬至日晷长到芒种日晷长的各数据依次排成一列得等差数列，数列的公差，因夏至与芒种相邻，且夏至日晷长最短，则夏至的日晷长为，又大雪与冬至相邻，且冬至日晷长最长，则大雪的日晷长为，显然夏至到大雪的日晷长依次排成一列是递增等差数列，首项为1.5尺，末项为12.5尺，共12项，所以一年中夏至到大雪的日晷长的和为(尺).故答案为：8416．已知正数满足，则的最小值为_________．【答案】【分析】运用同构函数研究其单调性可得，将求的最小值转化为求上的最小值，运用导数研究的最小值即可.【详解】因为，即，所以，所以.令，则，所以在上单调递增，所以，即，所以，令.则．令，解得：；令，解得：；所以在上单调递减，在上单调递增，所以.即的最小值为.故答案为：.【点睛】同构法的三种基本模式：①乘积型，如可以同构成，进而构造函数；②比商型，如可以同构成，进而构造函数；③和差型，如，同构后可以构造函数f或. 三、解答题17．已知是等差数列，满足，，数列满足，，且是等比数列.（1）求数列和的通项公式；（2）求数列的前项和.【答案】（1），；（2）【详解】试题分析：（1）利用等差数列，等比数列的通项公式先求得公差和公比，即得到结论;（2）利用分组求和法，由等差数列及等比数列的前n项和公式即可求得数列前n项和．试题解析：（Ⅰ）设等差数列{an}的公差为d，由题意得d= = = 3．∴an=a1+（n﹣1）d=3n设等比数列{bn﹣an}的公比为q，则q3= = =8，∴q=2，∴bn﹣an=（b1﹣a1）qn﹣1=2n﹣1， ∴bn=3n+2n﹣1（Ⅱ）由（Ⅰ）知bn=3n+2n﹣1， ∵数列{3n}的前n项和为n（n+1），数列{2n﹣1}的前n项和为1× = 2n﹣1，∴数列{bn}的前n项和为；【解析】1.等差数列性质的综合应用；2.等比数列性质的综合应用；3.数列求和． 18．春节期间，我国高速公路继续执行“节假日高速免费政策” ．某路桥公司为了解春节期间车辆出行的高峰情况，在某高速收费点发现大年初三上午9：20~10：40这一时间段内有600辆车通过，将其通过该收费点的时刻绘成频率分布直方图．其中时间段9：20~9：40记作区间，9：40~10：00记作，10：00~10：20记作，10：20~10：40记作，例如：10点04分，记作时刻64．(1)估计这600辆车在9：20~10：40时间段内通过该收费点的时刻的平均值（同一组中的数据用该组区间的中点值代表）；(2)为了对数据进行分析，现采用分层抽样的方法从这600辆车中抽取5辆，再从这5辆车中随机抽取3辆，则恰有1辆为9：20~10：00之间通过的概率是多少？【答案】(1)(2) 【分析】（1）运用频率分布直方图中平均数公式计算即可.（2）运用分层抽样比计算各段所抽取的车辆数，再运用列举法求古典概型的概率即可.【详解】（1）这600辆车在时间段内通过该收费点的时刻的平均值为，即：10点04分.（2）由题意知，时间段内抽取车辆数为，分别记为：，，时间段内抽取车辆数为，分别记为：，，时间段内抽取车辆数为，记为：，所以从这5辆车中随机抽取3辆的基本事件有：，，，，，，，，，共10个，恰有1辆为之间通过的基本事件有：，，，，，共有6个，所以恰有1辆为之间通过的概率为.19．如图，三棱柱中，侧面为菱形，的中点为，且平面．（1）证明：；（2）若，，，求三棱柱的高． 【答案】（1）证明见解析；（2）三棱柱的高为.【分析】（1）连接，则为与的交点，证明平面，可得；（2）作，垂足为，连接，作，垂足为，证明为等边三角形，求出到平面的距离，即可求三棱柱的高．【详解】（1）证明：连接，则为与的交点，侧面为菱形，，平面，平面，，，平面，平面，平面，；（2）解：作，垂足为，连接，作，垂足为，，，，平面，平面，平面，，，，平面，平面，，为等边三角形，，，，，由，可得，，为的中点，到平面的距离为，三棱柱的高． 20．已知函数．(1)求函数的极值；(2)求证：．【答案】(1)①当时，没有极值；②当时，有极大值，无极小值. (2)证明见解析 【分析】（1）求定义域后求，运用导数分类讨论与时单调性进而分析的极值. （2）运用对进行放缩及对数运算公式即可证明.【详解】（1），则定义域为，.①当时，恒成立，则为上的增函数，所以没有极值.②当时，由，得；由，得.所以在上单调递增，在上单调递减.故当时，有极大值，无极小值.综述：①当时，没有极值；②当时，有极大值，无极小值.（2）证明：取m＝1，由（1）知在上单调递减，所以.即,.令，得，即，分别取k＝n＋1，n＋2，…，n＋（n＋1），，可得．即成立．21．已知椭圆的左、右焦点分别为，，离心率，P为椭圆上一动点，面积的最大值为2.(1)求椭圆E的方程；(2)若C，D分别是椭圆E长轴的左、右端点，动点M满足，连结CM交椭圆于点N，O为坐标原点.证明：为定值；(3)平面内到两定点距离之比是常数的点的轨迹是圆.椭圆E的短轴上端点为A，点Q在圆上，求的最小值.【答案】(1)；(2)见解析；(3). 【分析】（1）结合离心率和面积的最大值列出关于的方程，解方程即可；（2）设直线CM方程，写出点M坐标，联立椭圆方程，求点N坐标，通过向量数量积计算即可；（3）设点坐标，借助点在圆上，将转化成，再借助椭圆定义将转化成，最后通过三点共线求出最小值.【详解】（1）当P为短轴端点时，的面积最大，，解得，故椭圆的方程为.（2）由（1）知，,设直线，，，联立整理得，由得，，,，故为定值4.（3）由题意，设，使，，整理得，又点Q在圆上，解得，由椭圆定义得，，当三点共线时，有最小值.【点睛】（1）关键在于建立的方程；（2）关键在于设出直线方程，联立得出点N坐标；（3）关键在于利用题目中给出的圆的定义将转化成，再结合椭圆定义，将问题简化成共线问题.22．在直角坐标系中，已知曲线的参数方程为（为参数），直线的方程为．以坐标原点为极点，轴的正半轴为极轴建立极坐标系．（1）求曲线和直线的极坐标方程；（2）若点在直线上且，射线与曲线相交于异于点的点，求的最小值．【答案】（1），；（2）.【分析】（1）将曲线的参数方程化为普通方程，再由普通方程与极坐标方程之间的转换关系可得出曲线的极坐标方程，直接利用普通方程与极坐标方程之间的转换关系可得出直线的极坐标方程；（2）设点的极坐标为，点的极坐标为，，求得，，利用三角恒等变换思想以及正弦函数的有界性可求得的最小值.【详解】（1）由曲线的参数方程，得曲线的普通方程为．即，由极坐标与直角坐标的互化公式，，得曲线的极坐标方程为.直线的极坐标方程为，即；（2）设点的极坐标为，点的极坐标为，其中．由（1）知，．．，．．当，即时，取得最小值．【点睛】方法点睛：在已知极坐标方程求曲线交点、距离、线段长等几何问题时，如果不能直接用极坐标解决，或用极坐标解决较麻烦，可将极坐标方程转化为直角坐标方程解决．23．已知函数，．（Ⅰ）当时，求不等式的解集；（Ⅱ）若关于的不等式的解集包含，求的取值集合．【答案】（Ⅰ）；（Ⅱ）.【分析】（Ⅰ）由时，得到函数，分类讨论，即可求得不等式的解集；（Ⅱ）由已知关于的不等式解集包含，等价于|在恒成立，进而得到在恒成立，由此可求解实数的取值范围．【详解】（Ⅰ）由题意，当时，函数，当时,，解得;当时，, 无解;当时， 解得；所以的解集为.（Ⅱ）由已知关于的不等式解集包含，等价于|在恒成立，因为，所以不等式恒成立即在恒成立，即，又，所以，故的取值集合是.【点睛】本题主要考查了含绝对值不等式的求解，以及含绝对值不等式的恒成立问题的求解，着重考查了转化思想，以及推理与运算能力，属于中档试题．