2023年青海省西宁市中考一模数学试题

西宁市2023年初中学考九年级调研测试(一)

数 学

考生注意：

1.本试卷满分120分，考试时间120分钟。

2.本试卷为试题卷，不允许作为答题卷使用，答题部分请在答题卡上作答，否则无效。

3.答题前，考生务必将自己的姓名、准考证号、考点、考场、座位号写在答题卡上。同时填写在

试卷上。

4.答选择题，用2B 铅笔把答题卡上对应题目的答案标号涂黑(如需改动，用橡皮擦干净后，再 选涂其他答案标号)。非选择题用0.5毫米的黑色字迹签字笔答在答题卡相应位置，字体工

整，笔迹清楚。作图必须用2B 铅笔作答，并请加黑加粗，描写清楚。

第I 卷 (选择题 共24分)

一、选择题(本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中，恰有一项是符合

题目要求的，请将正确选项的序号填涂在答题卡上.)

1.下列倡导节约的图案中，是轴对称图形的是

A                                              B                                               C                                           D

2.下列实数中，最大的数是

A.-π                           B.√25                          C.     I-8|                    D.  0

3.下列多边形中，内角和最大的是

A                                              B                                                 C                                           D

4.下列计算正确的是

A.(-x)²+x=2x³                                                 B.(-2x²y)³=-6x⁵y³

C.(-a)⁰÷a²=-a³                                                D.(- 1-x)²=x²+2x+1

数学试卷 · 第1页(共6页)

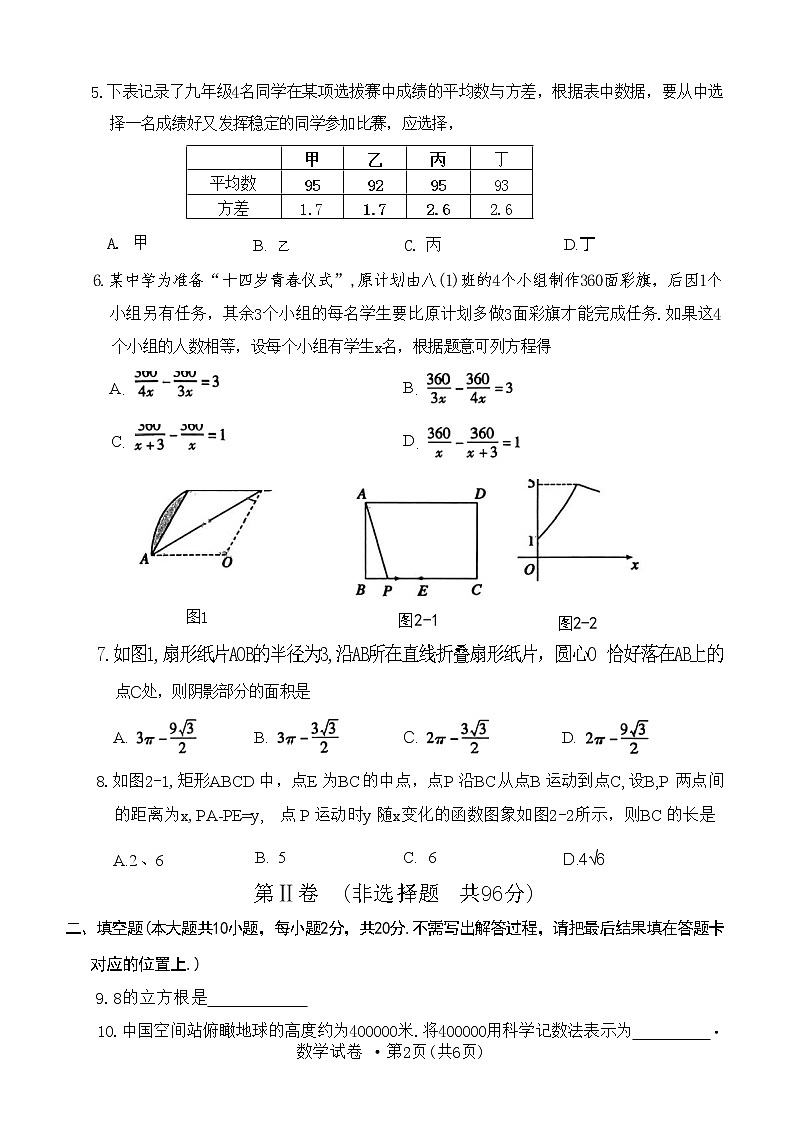
5.下表记录了九年级4名同学在某项选拔赛中成绩的平均数与方差，根据表中数据，要从中选

择一名成绩好又发挥稳定的同学参加比赛，应选择，

A. 甲            B.  乙                  C. 丙              D.丁

6.某中学为准备“十四岁青春仪式”,原计划由八(1)班的4个小组制作360面彩旗，后因1个 小组另有任务，其余3个小组的每名学生要比原计划多做3面彩旗才能完成任务.如果这4

个小组的人数相等，设每个小组有学生x名，根据题意可列方程得

.

.

图1

.

.

图2-1

7.如图1,扇形纸片AOB的半径为3,沿AB所在直线折叠扇形纸片，圆心O 恰好落在AB上的

点C处，则阴影部分的面积是

A.              B.                C.                D.

8.如图2-1,矩形ABCD 中，点E 为BC 的中点，点P 沿BC 从点B 运动到点C, 设B,P 两点间

的距离为x,PA-PE=y,   点 P 运动时y 随x变化的函数图象如图2-2所示，则BC 的长是

A.2 、6                      B.  5                            C.  6                              D.4√6

第Ⅱ卷 (非选择题 共96分)

二、填空题(本大题共10小题，每小题2分，共20分.不需写出解答过程，请把最后结果填在答题卡

对应的位置上.)

9.8的立方根是           

10.中国空间站俯瞰地球的高度约为400000米.将400000用科学记数法表示为         · 数学试卷 ·第2页(共6页)

11.若x-1有意义，则x的值可以是            (写出一个即可).

12.从 - 3, , √③,1,6中任取一个数作为k, 使反比例函数 的图象分别位于二、四象限

的概率是           

13.计算：(2x+1)(2x-1)-x(4x-1)=            

14.若 2ab²m+ 与α”-"b⁸ 的差仍是一个单项式，则m"=                       

15.如图3,△ABC 的边BC长为3 √2cm,将△ABC平移2cm得到△A'B'C', 且 BB' ⊥BC, 则阴影

部分的面积是           cm² .

图3                     图4                       图5

16.如图4,在平面直角坐标系中，点A在抛物线上运动，过点A 作AC⊥x 轴于

点 C, 以AC为对角线作矩形ABCD,连接BD,则对角线BD 的最小值为           

17.若等腰三角形的一边长是3,另两边的长是关于x的方程x²-8x+n=0   的两个根，则n 的

值为            

18.如图5,一束光线从点A(-6,4) 出发，经过y 轴上的点B 反射后经过点C(-2,0), 则反射

光线BC 所在直线的解析式为           

三、解答题(本大题共9小题，第19,20,21,22题每小题7分，第23,24题每小题8分，第25,26题 每小题10分，第27题12分，共76分.解答时将文字说明、证明过程或演算步骤写在答题卡相

应的位置上.)

19. (本题满分7分)                              20. (本题满分7分)

计算：(π-2)°- (-2)-¹+ | √③-2 |                 解方程

21. (本题满分7分)

先化简) ·,再从不等式2x-3≤1 的非负整数解中选一个使原式有意义的

数代入求值.

22. (本题满分7分)

2022年3月23日下午，中国空间站“天宫课堂”再度开课，“太空教师”翟志刚、王亚平、叶 光富演示了太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验.某校学生全员 观看了太空授课直播，为了解学生心中“最受启发的实验”(每人只选择一个实验)的情况，

随机抽取了部分学生进行调查，以下是根据调查结果绘制的统计图表的一部分.

根据以上信息，回答下列问题：

(1)本次调查的样本容量为      ,样本中认为“最受启发的实验是C” 的学生有     人；

(2)若该校共有1200名学生，请根据调查结果估计认为“最受启发的实验是B” 的学生有 多少人?

(3)某班的班主任为加深同学们的印象，让每位同学各自从这四个实验中随机抽取一个， 制作手抄报讲解实验现象背后的科学原理.小明和小丽分别从A,B,C,D   四个实验中 随机选取一个，请用画树状图或列表的方法求出两人选择同一个实验的概率，并列出 所有等可能的结果.

23. (本题满分8分)

如图6,点E,F 分别在等边△ABC 的边BC,AC 上，BE=CF,AE  与BF 交于点G.

(1)求证：△ABE ≌△BCF.

(2)求∠AGF的度数.

图6

数学试卷 · 第4页(共6页)

24. (本题满分8分)

如图7,已知一次函数 的图象与x轴交于点A, 与反比例函数，的图象在第

一象限交于点B, 过B 作 BC ⊥x 轴，垂足为C, 且BC=3.

(1)求k 的值；

(2)点P 在反比例函数的图象上，且△PAC的面积等于12, 请直接写出点P 的坐标.

图7

25. (本题满分10分)

如图8,AB是⊙O 的直径，C 为 BA 延长线上一点，CD是⊙O 的切线，D 为切点，连结BD,

过点O 作 OF ⊥AD于点E, 交 CD 于点F.

(1)求证：∠ADC= ∠AOF;

(2)若 ,BD=8, 求 OF 的长.

图8

26. (本题满分10分)

【阅读理解】

在学习了《锐角三角函数》这一章内容后，我们知道了30°,60°,45°这几个特殊角的三角函 数值，我们还能求出tan15°的值.

图9-1

图9-2

如图9- 1,在Rt △ABC 中，∠C=90°, ∠ABC=30°,AC=1,     延长CB 到点D, 使 DB=AB, 则

有∠D=15°

在Rt △ABC中  ∠ABC=30° ∴AB=BD=2           BC=√3

在Rt △ACD 中  

∴tan15°=2 √3.

数学试卷 · 第5页(共6页)

【实际应用】(1)2022年北京冬奥会持续点燃了群众们的冰雪热情，在“大力发展寒地 冰雪经济”的黄金发展时期，西宁市某滑雪场为满足青少年滑雪初学 者的需求，设计了一条滑道AB, 如图9-2所示，滑道的坡角∠B=15°, 水 平宽度BC=100m. 请根据以上材料提供的数据，求出图9-2中滑道的铅 直高度AC 是多少米?(结果取整数，参考数据 √3≈1.732).

【类比探究】(2)如果滑雪场准备再建一条坡角为22.5°的滑道，你能根据图9-3求出 tan22.5 °的值吗?

类比上面提供的方法，请你将下列探究过程补充完整：

解：Rt△ABC 中，∠C=90°,∠B=45°,AC=1

图9-3

27. (本题满分12分)

如图10,抛物线y=ax²+bx+2  与x轴交于点A(1,0) 和B(4,0).

(1)求抛物线的解析式；

(2)抛物线的对称轴交x轴于点E,点 F 是位于x轴上方对称轴上一点，FC//x 轴，与对称 轴右侧的抛物线交于点C,四边形OECF 是平行四边形，求点C 的坐标；

(3)在(2)的条件下，连接OC,x 轴上方的对称轴上是否存在点P,使△OCP 是直角三角形? 若存在，求出点P 的坐标；若不存在，请说明理由.

图r0

备用图

数学试卷 · 第6页(共6页)