历年高考数学真题精选40 频率分布直方图

这是一份历年高考数学真题精选40 频率分布直方图，共24页。
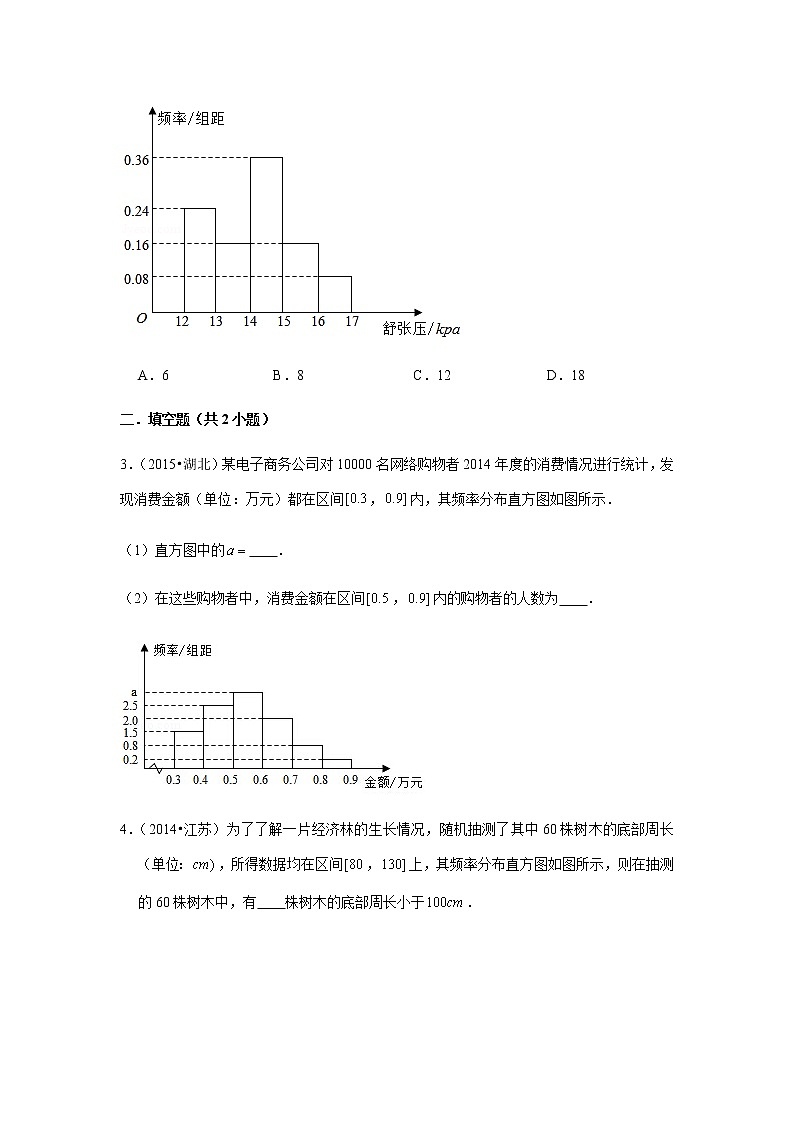
历年高考数学真题精选（按考点分类）专题40 频率分布直方图（学生版）一．选择题（共2小题）1．（2016•山东）某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是，，样本数据分组为，，，，，，，，，．根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是　　A．56 B．60 C．120 D．1402．（2014•山东）为了研究某药品的疗效，选取若干名志愿者进行临床试验．所有志愿者的舒张压数据（单位：的分组区间为，，，，，，，，，，将其按从左到右的顺序分别编号为第一组，第二组，，第五组．如图是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为　　A．6 B．8 C．12 D．18二．填空题（共2小题）3．（2015•湖北）某电子商务公司对10000名网络购物者2014年度的消费情况进行统计，发现消费金额（单位：万元）都在区间，内，其频率分布直方图如图所示．（1）直方图中的　　．（2）在这些购物者中，消费金额在区间，内的购物者的人数为　　．4．（2014•江苏）为了了解一片经济林的生长情况，随机抽测了其中60株树木的底部周长（单位：，所得数据均在区间，上，其频率分布直方图如图所示，则在抽测的60株树木中，有　　株树木的底部周长小于．三．解答题（共8小题）5．（2019•新课标Ⅲ）为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成、两组，每组100只，其中组小鼠给服甲离子溶液，组小鼠给服乙离子溶液．每只小鼠给服的溶液体积相同、摩尔浓度相同．经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比．根据试验数据分别得到如图直方图：记为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到（C）的估计值为0.70．（1）求乙离子残留百分比直方图中，的值；（2）分别估计甲、乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）．6．（2018•新课标Ⅰ）某家庭记录了未使用节水龙头50天的日用水量数据（单位：和使用了节水龙头50天的日用水量数据，得到频数分布表如下：未使用节水龙头50天的日用水量频数分布表 日用水量，，，，，，，频数13249265使用了节水龙头50天的日用水量频数分布表日用水量，，，，，，频数151310165（1）作出使用了节水龙头50天的日用水量数据的频率分布直方图；（2）估计该家庭使用节水龙头后，日用水量小于的概率；（3）估计该家庭使用节水龙头后，一年能节省多少水？（一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表）7．（2017•北京）某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：，，，，，，并整理得到如下频率分布直方图：（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间，内的人数；（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．8．（2017•新课标Ⅱ）海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：，其频率分布直方图如下：（1）记表示事件“旧养殖法的箱产量低于”，估计的概率；（2）填写下面列联表，并根据列联表判断是否有的把握认为箱产量与养殖方法有关： 箱产量箱产量旧养殖法  新养殖法  （3）根据箱产量的频率分布直方图，对两种养殖方法的优劣进行比较．附：0.0500.0100.0013.8416.63510.828．9．（2016•四川）我国是世界上严重缺水的国家．某市为了制定合理的节水方案，对居民用水情况进行了调查，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨）．将数据按照，，，，，，分成9组，制成了如图所示的频率分布直方图．（Ⅰ）求直方图中的值；（Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；（Ⅲ）估计居民月均水量的中位数．10．（2016•北京）某市居民用水拟实行阶梯水价，每人月用水量中不超过立方米的部分按4元立方米收费，超出立方米的部分按10元立方米收费，从该市随机调查了10000位居民，获得了他们某月的用水量数据，整理得到如图频率分布直方图：（1）如果为整数，那么根据此次调查，为使以上居民在该月的用水价格为4元立方米，至少定为多少？（2）假设同组中的每个数据用该组区间的右端点值代替，当时，估计该市居民该月的人均水费．11．（2015•广东）某城市100户居民的月平均用电量（单位：度），以，，，，，，，，，，，，，分组的频率分布直方图如图． （1）求直方图中的值；（2）求月平均用电量的众数和中位数；（3）在月平均用电量为，，，，，，，的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在，的用户中应抽取多少户？12．（2015•新课标Ⅱ）某公司为了解用户对其产品的满意度，从，两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到地区用户满意度评分的频率分布直方图和地区用户满意度评分的频数分布表地区用户满意度评分的频数分布表满意度评分分组，，，，，频数2814106（1）做出地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大？说明理由．
历年高考数学真题精选（按考点分类）专题40 频率分布直方图（教师版）一．选择题（共2小题）1．（2016•山东）某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是，，样本数据分组为，，，，，，，，，．根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是　　A．56 B．60 C．120 D．140【答案】D【解析】自习时间不少于22.5小时的频率为：，故自习时间不少于22.5小时的频数为：2．（2014•山东）为了研究某药品的疗效，选取若干名志愿者进行临床试验．所有志愿者的舒张压数据（单位：的分组区间为，，，，，，，，，，将其按从左到右的顺序分别编号为第一组，第二组，，第五组．如图是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为　　A．6 B．8 C．12 D．18【答案】C【解析】由直方图可得分布在区间第一组与第二组共有20人，分布在区间第一组与第二组的频率分别为0.24，0.16，所以第一组有12人，第二组8人，第三组的频率为0.36，所以第三组的人数：18人，第三组中没有疗效的有6人，第三组中有疗效的有12人．二．填空题（共2小题）3．（2015•湖北）某电子商务公司对10000名网络购物者2014年度的消费情况进行统计，发现消费金额（单位：万元）都在区间，内，其频率分布直方图如图所示．（1）直方图中的　　．（2）在这些购物者中，消费金额在区间，内的购物者的人数为　　．【答案】（1）3 （2）6000【解析】（1）由题意，根据直方图的性质得，解得（2）由直方图得4．（2014•江苏）为了了解一片经济林的生长情况，随机抽测了其中60株树木的底部周长（单位：，所得数据均在区间，上，其频率分布直方图如图所示，则在抽测的60株树木中，有　　株树木的底部周长小于．【答案】24【解析】由频率分布直方图知：底部周长小于的频率为，底部周长小于的频数为（株．三．解答题（共8小题）5．（2019•新课标Ⅲ）为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成、两组，每组100只，其中组小鼠给服甲离子溶液，组小鼠给服乙离子溶液．每只小鼠给服的溶液体积相同、摩尔浓度相同．经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比．根据试验数据分别得到如图直方图：记为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到（C）的估计值为0.70．（1）求乙离子残留百分比直方图中，的值；（2）分别估计甲、乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）．解：（1）为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到（C）的估计值为0.70．则由频率分布直方图得：，解得乙离子残留百分比直方图中，．（2）估计甲离子残留百分比的平均值为：．乙离子残留百分比的平均值为：．6．（2018•新课标Ⅰ）某家庭记录了未使用节水龙头50天的日用水量数据（单位：和使用了节水龙头50天的日用水量数据，得到频数分布表如下：未使用节水龙头50天的日用水量频数分布表 日用水量，，，，，，，频数13249265使用了节水龙头50天的日用水量频数分布表日用水量，，，，，，频数151310165（1）作出使用了节水龙头50天的日用水量数据的频率分布直方图；（2）估计该家庭使用节水龙头后，日用水量小于的概率；（3）估计该家庭使用节水龙头后，一年能节省多少水？（一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表）【解答】解：（1）根据使用了节水龙头50天的日用水量频数分布表，作出使用了节水龙头50天的日用水量数据的频率分布直方图，如下图：（2）根据频率分布直方图得：该家庭使用节水龙头后，日用水量小于的概率为：．（3）由题意得未使用水龙头50天的日均水量为：，使用节水龙头50天的日均用水量为：，估计该家庭使用节水龙头后，一年能节省：．7．（2017•北京）某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：，，，，，，并整理得到如下频率分布直方图：（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间，内的人数；（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．解：（Ⅰ）由频率分布直方图知：分数小于70的频率为：故从总体的400名学生中随机抽取一人，估计其分数小于70的概率为0.4；（Ⅱ）已知样本中分数小于40的学生有5人，故样本中分数小于40的频率为：0.05，则分数在区间，内的频率为：，估计总体中分数在区间，内的人数为人，（Ⅲ）样本中分数不小于70的频率为：0.6，由于样本中分数不小于70的男女生人数相等．故分数不小于70的男生的频率为：0.3，由样本中有一半男生的分数不小于70，故男生的频率为：0.6，即女生的频率为：0.4，即总体中男生和女生人数的比例约为：．8．（2017•新课标Ⅱ）海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：，其频率分布直方图如下：（1）记表示事件“旧养殖法的箱产量低于”，估计的概率；（2）填写下面列联表，并根据列联表判断是否有的把握认为箱产量与养殖方法有关： 箱产量箱产量旧养殖法  新养殖法  （3）根据箱产量的频率分布直方图，对两种养殖方法的优劣进行比较．附：0.0500.0100.0013.8416.63510.828．解：（1）根据题意，由旧养殖法的频率分布直方图可得：（A）；（2）根据题意，补全列联表可得： 箱产量箱产量总计旧养殖法6238100新养殖法3466100总计96104200则有，故有的把握认为箱产量与养殖方法有关；（3）由频率分布直方图可得：旧养殖法100个网箱产量的平均数；新养殖法100个网箱产量的平均数；比较可得：，故新养殖法更加优于旧养殖法．9．（2016•四川）我国是世界上严重缺水的国家．某市为了制定合理的节水方案，对居民用水情况进行了调查，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨）．将数据按照，，，，，，分成9组，制成了如图所示的频率分布直方图．（Ⅰ）求直方图中的值；（Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；（Ⅲ）估计居民月均水量的中位数．解：，整理可得：，解得：．估计全市居民中月均用水量不低于3吨的人数为3.6万，理由如下：由已知中的频率分布直方图可得月均用水量不低于3吨的频率为，又样本容量为30万，则样本中月均用水量不低于3吨的户数为万．（Ⅲ）根据频率分布直方图，得；，，中位数应在，组内，设出未知数，令，解得；中位数是．10．（2016•北京）某市居民用水拟实行阶梯水价，每人月用水量中不超过立方米的部分按4元立方米收费，超出立方米的部分按10元立方米收费，从该市随机调查了10000位居民，获得了他们某月的用水量数据，整理得到如图频率分布直方图：（1）如果为整数，那么根据此次调查，为使以上居民在该月的用水价格为4元立方米，至少定为多少？（2）假设同组中的每个数据用该组区间的右端点值代替，当时，估计该市居民该月的人均水费．解：（1）由频率分布直方图得：用水量在，的频率为0.1，用水量在，的频率为0.15，用水量在，的频率为0.2，用水量在，的频率为0.25，用水量在，的频率为0.15，用水量在，的频率为0.05，用水量在，的频率为0.05，用水量在，的频率为0.05，用水量小于等于3立方米的频率为，为使以上居民在该用的用水价为4元立方米，至少定为3立方米．（2）当时，该市居民的人均水费为：，当时，估计该市居民该月的人均水费为10.5元．11．（2015•广东）某城市100户居民的月平均用电量（单位：度），以，，，，，，，，，，，，，分组的频率分布直方图如图． （1）求直方图中的值；（2）求月平均用电量的众数和中位数；（3）在月平均用电量为，，，，，，，的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在，的用户中应抽取多少户？解：（1）由直方图的性质可得，解方程可得，直方图中的值为0.0075；（2）月平均用电量的众数是，，月平均用电量的中位数在，内，设中位数为，由可得，月平均用电量的中位数为224；（3）月平均用电量为，的用户有，月平均用电量为，的用户有，月平均用电量为，的用户有，月平均用电量为，的用户有，抽取比例为，月平均用电量在，的用户中应抽取户．12．（2015•新课标Ⅱ）某公司为了解用户对其产品的满意度，从，两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到地区用户满意度评分的频率分布直方图和地区用户满意度评分的频数分布表地区用户满意度评分的频数分布表满意度评分分组，，，，，频数2814106（1）做出地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大？说明理由．解：（Ⅰ）通过两个地区用户满意度评分的频率分布直方图可以看出，地区用户满意度评分的平均值高于地区用户满意度评分的平均值， 地区的用户满意度评分的比较集中，而地区的用户满意度评分的比较分散．（Ⅱ）地区用户的满意度等级为不满意的概率大．记表示事件：“地区用户的满意度等级为不满意”， 表示事件：“地区用户的满意度等级为不满意”，由直方图得得地区用户的满意度等级为不满意的概率大．