资料中包含下列文件,点击文件名可预览资料内容





还剩13页未读,
继续阅读
所属成套资源:7年级人教版数学上册(秋季班)同步培优题典
成套系列资料,整套一键下载
7年级数学上册同步培优题典 专题4.9 第4章几何图形初步单元测试(培优卷)(人教版)
展开
这是一份7年级数学上册同步培优题典 专题4.9 第4章几何图形初步单元测试(培优卷)(人教版),文件包含7年级数学上册同步培优题典专题49第4章几何图形初步单元测试培优卷教师版人教版docx、7年级数学上册同步培优题典专题49第4章几何图形初步单元测试培优卷学生版人教版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
初中数学培优措施和方法
1、拓宽解题思路。数学解题不要局限于本题,而要做到举一反三、多思多想
2、细节决定成败。审题的细节、知识理解的细节、运用公式的细节、忽视检验的细节等,细节决定成败。
3、制作错题集。收集自己的错误,分门别类,没事时就翻一翻,看一看,自警一番,肯定会有很大的收获。
4、查自己欠缺的知识。关键的是做好知识准备,检查漏洞;其次是对解题常犯错误的准备
5、把好的做法形成习惯。注意书写规范,重要步骤不能丢,丢步骤等于丢分。
6、主动思考,全心投入。听课过程中,要主动思考,这样遇到实际问题时,会应用所学的知识去解答问题。
专题4.9第4章几何图形初步单元测试(培优卷)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分120分,试题共24题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020春•肇东市期末)下列几何体中,是棱锥的为( )
A. B.
C. D.
【分析】根据各个几何体的特征,得出棱锥的几何体.
【解析】选项中的四个几何体的名称分别为:圆柱,圆锥,四棱柱,四棱锥,
故选:D.
2.(2019秋•沙坪坝区校级期末)用一个平面去截一个圆锥,截面的形状不可能是( )
A.圆 B.矩形 C.椭圆 D.三角形
【分析】根据圆锥的形状特点判断即可.
【解析】过圆锥的顶点的截面是三角形,平行于圆锥的底面的截面是圆,不平行于圆锥的底面的截面是椭圆,
截面不可能是矩形,故B符合题意;
故选:B.
3.(2017秋•庆云县期末)下列说法正确的是( )
A.射线AB与射线BA表示同一条射线
B.连接两点的线段叫做这两点的距离
C.平角是一条直线
D.若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3
【分析】根据射线的定义,两点间的距离的概念,平角的定义,余角的性质即可作出选择.
【解析】A、射线AB与射线BA表示不同的两条射线,故本选项错误;
B、连接两点的线段的长度叫做这两点的距离,故本选项错误;
C、平角的两条边在一条直线上,故本选项错误;
D、若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3是正确的,故本选项正确.
故选:D.
4.(2018秋•高阳县期末)若∠1=40.4°,∠2=40°4′,则∠1与∠2( )
A.∠1<∠2 B.∠1>∠2 C.∠1=∠2 D.无法确定
【分析】首先统一单位,利用1°=60′,可得∠1=40.4°=40°24′,再进一步与∠2比较得出答案即可.
【解析】∵∠1=40.4°=40°24′,∠2=40°4′,
∴∠1>∠2.
故选:B.
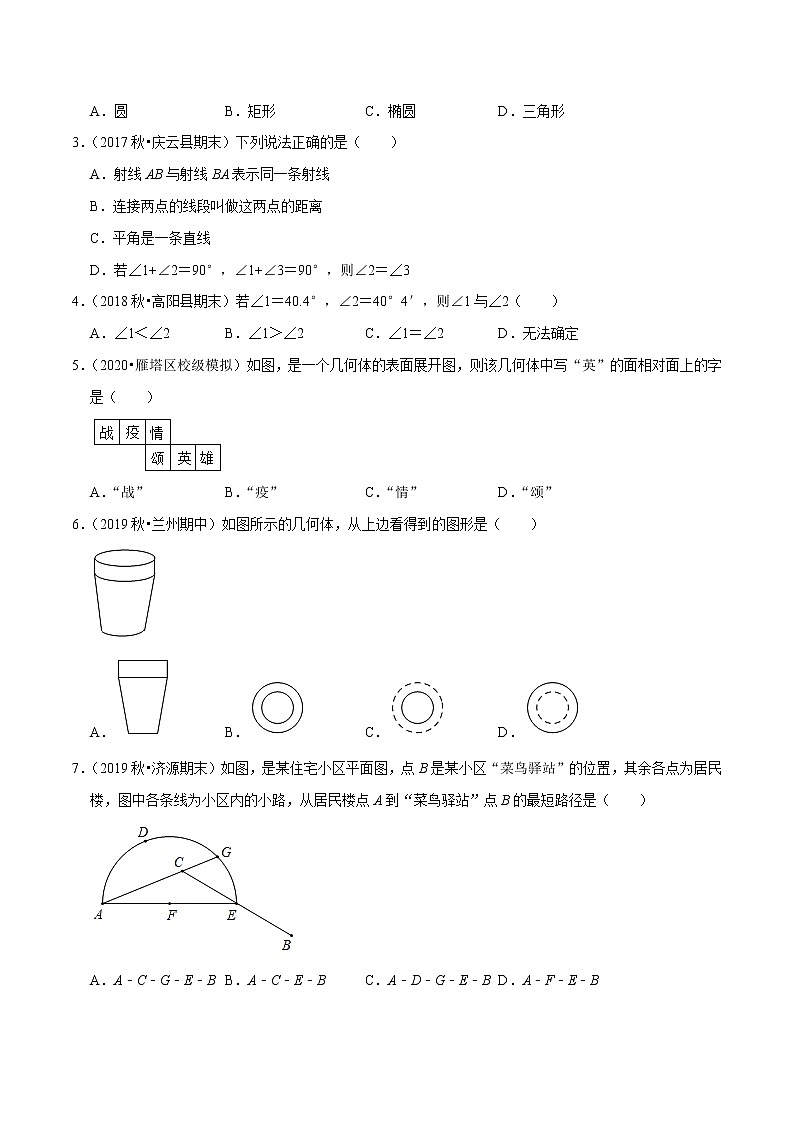
5.(2020•雁塔区校级模拟)如图,是一个几何体的表面展开图,则该几何体中写“英”的面相对面上的字是( )
A.“战” B.“疫” C.“情” D.“颂”
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,
“战”与“情”是相对面,
“疫”与“英”是相对面,
“颂”与“雄”是相对面.
故选:B.
6.(2019秋•兰州期中)如图所示的几何体,从上边看得到的图形是( )
A. B. C. D.
【分析】从上面看,能看到的是圆形,但看不到的底面的轮廓线用虚线表示.
【解析】从上面看到的是圆形,相当于看一个杯子的俯视图,因此选择D,
故选:D.
7.(2019秋•济源期末)如图,是某住宅小区平面图,点B是某小区“菜鸟驿站”的位置,其余各点为居民楼,图中各条线为小区内的小路,从居民楼点A到“菜鸟驿站”点B的最短路径是( )
A.A﹣C﹣G﹣E﹣B B.A﹣C﹣E﹣B C.A﹣D﹣G﹣E﹣B D.A﹣F﹣E﹣B
【分析】由两点之间线段最短可解决问题.
【解析】由题意可得BE是必须经过的路段,
∴由两点之间线段最短,可得点A到点E的最短路径A﹣F﹣E,
∴从居民楼点A到“菜鸟驿站”点B的最短路径是A﹣F﹣E﹣B,
故选:D.
8.(2019秋•无棣县期末)如图,点C、D为线段AB上两点,AC+BD=6,且AD+BC=75AB,则CD等于( )
A.10 B.8 C.6 D.4
【分析】根据线段的和差计算即可.
【解析】∵AD+BC=75AB,
∴5(AD+BC)=7AB,
∴5(AC+CD+CD+BD)=7(AC+CD+BD),
∵AC+BD=6,
∴CD=4,
故选:D.
9.(2019秋•蚌埠期末)如图,∠AOD=60°,∠AOB:∠BOC=1:4,OD平分∠BOC,则∠AOC的度数为( )
A.20° B.80° C.100° D.120°
【分析】由题意设∠AOB为x,∠BOC为3x,再根据角的平分线的性质得出∠BOD=12∠BOC=2x,于是得x+2x=60°,求得x,再求∠AOC的度数即可.
【解析】∵∠AOB:∠BOC=1:4,
∴设∠AOB为x,∠BOC为4x,
∵OD平分∠BOC,
∴∠BOD=12∠BOC=2x,
∵∠AOD=60°,
∴x+2x=60°,
∴x=20°,
4x=80°,
∴∠AOC=∠AOB+∠BOC=20°+80°=100°,
故选:C.
10.(2020•新华区一模)按图1~图4的步骤作图,下列结论错误的是( )
A.12∠AOB=∠AOP B.∠AOP=∠BOP
C.2∠BOP=∠AOB D.∠BOP=2∠AOP
【分析】根据角平分线的定义对各选项进行逐一分析即可.
【解析】∵OP是∠AOB的平分线,
∴∠AOB=2∠AOP=2∠BOP,
∠AOP=∠BOP=12∠AOB,
∴选项A、B、C均正确,选项D错误.
故选:D.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋•宝安区期末)60°36′= 60.6 度.
【分析】依据度分秒的换算即可得到结果.
【解析】36′=0.6°,
∴60°36′=60.6°,
故答案为:60.6.
12.(2019秋•顺城区期末)点A、B、C是同一直线上的三个点,若AB=8cm,BC=3cm,则AC= 11或5 cm.
【分析】分点B在点A、C之间和点C在点A、B之间两种情况讨论.
【解析】(1)点B在点A、C之间时,AC=AB+BC=8+3=11cm;
(2)点C在点A、B之间时,AC=AB﹣BC=8﹣3﹣5cm.
∴AC的长度为11cm或5cm.
13.(2019秋•石景山区期末)如图,①~④展开图中,能围成三棱柱的是 ② .
【分析】依据展开图的特征,即可得到围成的几何体的类型.
【解析】图①能围成圆锥;图②能围成三棱柱;图③能围成正方体;图④能围成四棱锥;
故答案为:②.
14.(2019秋•青川县期末)如图所示,两个直角三角形的直角顶点重合,如果∠AOD=118°,那么∠BOC= 62° .
【分析】根据题意得到∠AOB=∠COD=90°,再计算∠BOD=∠AOD﹣90°=28°,然后根据∠BOC=∠COD﹣∠BOD进行计算即可.
【解析】∵∠AOB=∠COD=90°,
而∠AOD=118°,
∴∠BOD=∠AOD﹣90°=28°,
∴∠BOC=∠COD﹣∠BOD=90°﹣28°=62°.
故答案为:62°.
15.(2019秋•沈河区期末)已知线段MN=16cm,点P为任意一点,那么线段MP与NP和的最小值是 16 cm.
【分析】根据线段的性质解答即可.
【解析】如图所示:
所以线段MP与NP和的最小值是16cm,
故答案为;16
16.(2019秋•通州区期末)已知∠AOB=60°,以点O为端点作射线OC,使∠BOC=20°,再作∠AOC的平分线OD,则∠AOD的度数为 20°或40° .
【分析】考虑线段OC在角的内部和外部两种情况,每一种情况都用角的定义和角平分的定义求解,经计算结果为20°或40°.
【解析】(1)当OC在∠AOB的内部时,
如图1所示:
∵∠BOC=20°,∠AOB=60°,
∠AOB=∠AOC+∠BOC,
∴∠AOC=60°﹣20°=40°,
又∵OD是∠AOC的平分线,
∴∠AOD=∠COD=12∠AOC=20°;
(2)当OC在∠AOB的外部时,
如图2所示:
∵∠AOC=∠AOB+∠BOC,
∠AOB=60°,∠BOC=20°,
∴AOC=80°,
又∵OD是∠AOC的平分线,
∴∠AOD=∠COD=12∠AOC=40°;
综合所述∠AOD的度数有两个,
故答案为20°或40°.
17.(2019秋•茂名期中)某几何体从三个方向看到的图形分别如图,则该几何体的体积为 3π .
【分析】由主视图和俯视图可得此几何体为柱体,根据左视图是圆及圆心可判断出此几何体为圆柱.
【解析】由三视图可得,此几何体为圆柱,
所以圆柱的体积为3×π⋅(22)2=3π,
故答案为:3π
18.(2020春•宜春期末)如图,∠AOC=∠BOD=90°,∠AOB=70°,在∠AOB内画一条射线OP得到的图中有m对互余的角,其中∠AOP=x°,且满足0<x<50,则m= 3或4或6 .
【分析】分三种情况下:①∠AOP=35°,②∠AOP=20°,③0<x<50中的其余角,根据互余的定义找出图中互余的角即可求解.
【解析】①∠AOP=35°,互余的角有∠AOP与∠COP,∠BOP与∠COP,∠AOB与∠COB,∠COD与∠COB,一共4对;
②∠AOP=20°,互余的角有∠AOP与∠COP,∠AOP与∠AOB,∠AOP与∠COD,∠COD与∠COB,∠AOB与∠COB,∠COP与∠COB,一共6对;
③0<x<50中35°与20°的其余角,互余的角有∠AOP与∠COP,∠AOB与∠COB,∠COD与∠COB,一共3对.
则m=3或4或6.
故答案为:3或4或6.
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2019秋•长葛市期末)如图,已知A、B、C、D四点,根据下列要求画图:
(1)画直线AB、射线AD;
(2)画∠CDB;
(3)找一点P,使点P既在AC上又在BD上.
【分析】(1)利用直线以及射线的定义画出图形即可;
(2)利用角的定义作射线DC,DB即可;
(3)连接AC,BD即可得出P点.
【解析】(1)如图所示:直线AB、射线AD即为所求;
(2)如图所示:∠CDB即为所求;
(3)如图所示:点P即为所求.
20.(2020•江北区模拟)将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.
(1)以下两个方格图中的阴影部分能表示立方体表面展开图的是 A (填A或B).
(2)在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示)
(3)如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)
【分析】(1)有“田”字格的展开图都不能围成正方体,据此可排除B,从而得出答案;
(2)可利用“1、3、2”作图(答案不唯一);
(3)根据裁剪线裁剪,再展开.
【解析】(1)两个方格图中的阴影部分能表示立方体表面展开图的是A,
故答案为:A.
(2)立方体表面展开图如图所示:
(3)将其表面展开图画在方格图中如图所示:
21.已知∠1是∠2的2倍,∠1的余角的3倍与∠2的补角相等,求∠1、∠2的度数.
【分析】利用题中“∠1是∠2的2倍,∠1的余角的3倍与∠2的补角相等”作为相等关系列方程求解即可.
【解析】设∠2是x,则∠1=2x,
则3(90°﹣2x)=180°﹣x,
解得x=18°.
故∠1=36°,∠2=18°.
22.(2019秋•襄州区期末)已知:如图,AB=18cm,点M是线段AB的中点,点C把线段MB分成MC:CB=2:1的两部分,求线段AC的长.
请补充完成下列解答:
解:∵M是线段AB的中点,AB=18cm,
∴AM=MB= 12 AB= 9 cm.
∵MC:CB=2:1,
∴MC= 23 MB= 6 cm.
∴AC=AM+ MC = 9 + 6 = 15 cm.
【分析】根据线段中点的性质,可得AM,根据线段的比,可得MC,根据线段的和差,可得答案.
【解析】∵M是线段AB的中点,且AB=18cm,
∴AM=MB=12AB=9cm.
∵MC:CB=2:1,
∴MC=23MB=6cm.
∵AC=AM+MC,
∴AC=9+6=15cm,
故答案为:12,9,23,6,MC,9,6,15.
23.(2019秋•蒙城县期末)如图,O为直线AB上一点,OM是∠AOC的角平分线,ON是∠COB的平分线
(1)指出图中所有互为补角的角.
(2)求∠MON的度数.
(3)指出图中所有互为余角的角.
【分析】(1)根据如果两个角的和等于180°(平角),就说这两个角互为补角进行分析即可;
(2)根据角平分线定义求出∠COM=12∠AOC,∠CON=12∠BOC,求出∠MON=∠COM+∠CON=12(∠AOC+∠BOC),把∠AOC+∠BOC=180°代入求出即可;
(3)根据如果两个角的和等于90°(直角),就说这两个角互为余角进行分析即可.
【解析】(1)∠AOM与∠MOB,∠AOC与∠BOC,∠AON与∠BON,∠COM与∠MOB,∠CON与∠AON;
(2)∵∠AOC的平分线是OM,∠BOC的平分线是ON,
∴∠COM=12∠AOC,∠CON=12∠BOC,
∵∠AOB=∠AOC+∠BOC=180°,
∴∠MON=∠COM+∠CON
=12(∠AOC+∠BOC)
=12×180°
=90°,
(3)∠AOM与∠BON,∠COM与∠BON,∠CON与∠AOM,∠CON与∠COM.
24.(2019秋•鄄城县期末)如图,已知线段AB、a、b.
(1)请用尺规按下列要求作图:(不要求写作法,但要保留作图痕迹)
①延长线段AB到C,使BC=a;
②反向延长线段AB到D,使AD=b.
(2)在(1)的条件下,如果AB=8cm,a=6m,b=10cm,且点E为CD的中点,求线段AE的长度.
【分析】(1)根据题意画出图形即可;
(2)根据线段的画出和线段的中点的定义即可得到结论.
【解析】(1)①如图所示,线段BC即为所求,
②如图所示,线段AD即为所求;
(2)∵AB=8cm,a=6m,b=10cm,
∴CD=8+6+10=24cm,
∵点E为CD的中点,
∴DE=12DC=12cm,
∴AE=DE﹣AD=12﹣10=2cm.
25.(2019秋•琅琊区期末)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 北偏东70° ;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
【分析】(1)先求出∠AOB=55°,再求得∠NOC的度数,即可确定OC的方向;
(2)根据∠AOB=55°,∠AOC=∠AOB,得出∠BOC=110°,进而求出∠COD的度数;
(3)根据射线OE平分∠COD,即可求出∠COE=35°再利用∠AOC=55°求出答案即可.
【解析】(1)∵OB的方向是北偏西40°,OA的方向是北偏东15°,
∴∠NOB=40°,∠NOA=15°,
∴∠AOB=∠NOB+∠NOA=55°,
∵∠AOB=∠AOC,
∴∠AOC=55°,
∴∠NOC=∠NOA+∠AOC=70°,
∴OC的方向是北偏东70°;
故答案为:北偏东70°;
(2)∵∠AOB=55°,∠AOC=∠AOB,
∴∠BOC=110°.
又∵射线OD是OB的反向延长线,
∴∠BOD=180°.
∴∠COD=180°﹣110°=70°.
(3)∵∠COD=70°,OE平分∠COD,
∴∠COE=35°.
∵∠AOC=55°.
∴∠AOE=90°.
26.(2020春•南岗区期末)已知,在∠AOB内部作射线OC,OD平分∠BOC,∠AOD+∠COD=120°.
(1)如图1,求∠AOB的度数;
(2)如图2,在∠AOB的外部和∠BOD的内部分别作射线OE、OF,已知∠COD=2∠BOF+∠BOE,求证:OF平分∠DOE;
(3)如图3,在(2)的条件下,在∠COD内部作射线OM,当∠BOM=4∠COM,∠BOE=1110∠AOC时,求∠MOF的度数.
【分析】(1)根据OD平分∠BOC,得∠BOD=∠COD,再由∠AOD+∠COD=120°,得∠AOD+∠BOD=120°,即∠AOB=120°;
(2)根据OD平分∠BOC,得∠BOD=∠COD,再由∠COD=2∠BOF+∠BOE,得∠BOD=2∠BOF+∠BOE,可得∠DOF=∠BOD﹣∠BOF=2∠BOF+∠BOE﹣∠BOF=∠BOF+∠BOE=∠EOF,即可得出结论;
(3)设∠AOC=10α,则∠BOE=11α,由∠AOB=120°得∠BOC=∠AOB﹣∠AOC=120°﹣10α,根据OD平分∠BOC,得∠COD=∠BOD=12∠BOC=60°﹣5α,再由∠BOM=4∠COM,得∠COM=15∠BOC=15(120°﹣10α)=24°﹣2α,可得∠DOM=∠COD﹣∠COM=36°﹣3α,∠DOE=∠BOD+∠BOE=60°+6α,根据OF平分∠DOE可得∠DOF=12∠DOE=12(60°+6α)=30°+3α,由∠MOF=∠DOM+∠DOF可得结果.
【解答】(1)解:∵OD平分∠BOC,
∴∠BOD=∠COD,
∵∠AOD+∠COD=120°,
∴∠AOD+∠BOD=120°,
即∠AOB=120°;
(2)证明:∵OD平分∠BOC,
∴∠BOD=∠COD,
∵∠COD=2∠BOF+∠BOE,
∴∠BOD=2∠BOF+∠BOE,
∴∠DOF=∠BOD﹣∠BOF=2∠BOF+∠BOE﹣∠BOF=∠BOF+∠BOE=∠EOF,
∴OF平分∠DOE;
(3)解:设∠AOC=10α,则∠BOE=11α,
∵∠AOB=120°,
∴∠BOC=∠AOB﹣∠AOC=120°﹣10α,
∵OD平分∠BOC,
∴∠COD=∠BOD=12∠BOC=60°﹣5α,
∵∠BOM=4∠COM,
∴∠COM=15∠BOC=15(120°﹣10α)=24°﹣2α,
∴∠DOM=∠COD﹣∠COM=(60°﹣5α)﹣(24°﹣2α)=36°﹣3α,
∴∠DOE=∠BOD+∠BOE=(60°﹣5α)+11α=60°+6α,
∵OF平分∠DOE,
∴∠DOF=12∠DOE=12(60°+6α)=30°+3α,
∴∠MOF=∠DOM+∠DOF=(36°﹣3α)+(30°+3α)=66°.
初中数学培优措施和方法
1、拓宽解题思路。数学解题不要局限于本题,而要做到举一反三、多思多想
2、细节决定成败。审题的细节、知识理解的细节、运用公式的细节、忽视检验的细节等,细节决定成败。
3、制作错题集。收集自己的错误,分门别类,没事时就翻一翻,看一看,自警一番,肯定会有很大的收获。
4、查自己欠缺的知识。关键的是做好知识准备,检查漏洞;其次是对解题常犯错误的准备
5、把好的做法形成习惯。注意书写规范,重要步骤不能丢,丢步骤等于丢分。
6、主动思考,全心投入。听课过程中,要主动思考,这样遇到实际问题时,会应用所学的知识去解答问题。
专题4.9第4章几何图形初步单元测试(培优卷)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分120分,试题共24题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020春•肇东市期末)下列几何体中,是棱锥的为( )
A. B.
C. D.
【分析】根据各个几何体的特征,得出棱锥的几何体.
【解析】选项中的四个几何体的名称分别为:圆柱,圆锥,四棱柱,四棱锥,
故选:D.
2.(2019秋•沙坪坝区校级期末)用一个平面去截一个圆锥,截面的形状不可能是( )
A.圆 B.矩形 C.椭圆 D.三角形
【分析】根据圆锥的形状特点判断即可.
【解析】过圆锥的顶点的截面是三角形,平行于圆锥的底面的截面是圆,不平行于圆锥的底面的截面是椭圆,
截面不可能是矩形,故B符合题意;
故选:B.
3.(2017秋•庆云县期末)下列说法正确的是( )
A.射线AB与射线BA表示同一条射线
B.连接两点的线段叫做这两点的距离
C.平角是一条直线
D.若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3
【分析】根据射线的定义,两点间的距离的概念,平角的定义,余角的性质即可作出选择.
【解析】A、射线AB与射线BA表示不同的两条射线,故本选项错误;
B、连接两点的线段的长度叫做这两点的距离,故本选项错误;
C、平角的两条边在一条直线上,故本选项错误;
D、若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3是正确的,故本选项正确.
故选:D.
4.(2018秋•高阳县期末)若∠1=40.4°,∠2=40°4′,则∠1与∠2( )
A.∠1<∠2 B.∠1>∠2 C.∠1=∠2 D.无法确定
【分析】首先统一单位,利用1°=60′,可得∠1=40.4°=40°24′,再进一步与∠2比较得出答案即可.
【解析】∵∠1=40.4°=40°24′,∠2=40°4′,
∴∠1>∠2.
故选:B.
5.(2020•雁塔区校级模拟)如图,是一个几何体的表面展开图,则该几何体中写“英”的面相对面上的字是( )
A.“战” B.“疫” C.“情” D.“颂”
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,
“战”与“情”是相对面,
“疫”与“英”是相对面,
“颂”与“雄”是相对面.
故选:B.
6.(2019秋•兰州期中)如图所示的几何体,从上边看得到的图形是( )
A. B. C. D.
【分析】从上面看,能看到的是圆形,但看不到的底面的轮廓线用虚线表示.
【解析】从上面看到的是圆形,相当于看一个杯子的俯视图,因此选择D,
故选:D.
7.(2019秋•济源期末)如图,是某住宅小区平面图,点B是某小区“菜鸟驿站”的位置,其余各点为居民楼,图中各条线为小区内的小路,从居民楼点A到“菜鸟驿站”点B的最短路径是( )
A.A﹣C﹣G﹣E﹣B B.A﹣C﹣E﹣B C.A﹣D﹣G﹣E﹣B D.A﹣F﹣E﹣B
【分析】由两点之间线段最短可解决问题.
【解析】由题意可得BE是必须经过的路段,
∴由两点之间线段最短,可得点A到点E的最短路径A﹣F﹣E,
∴从居民楼点A到“菜鸟驿站”点B的最短路径是A﹣F﹣E﹣B,
故选:D.
8.(2019秋•无棣县期末)如图,点C、D为线段AB上两点,AC+BD=6,且AD+BC=75AB,则CD等于( )
A.10 B.8 C.6 D.4
【分析】根据线段的和差计算即可.
【解析】∵AD+BC=75AB,
∴5(AD+BC)=7AB,
∴5(AC+CD+CD+BD)=7(AC+CD+BD),
∵AC+BD=6,
∴CD=4,
故选:D.
9.(2019秋•蚌埠期末)如图,∠AOD=60°,∠AOB:∠BOC=1:4,OD平分∠BOC,则∠AOC的度数为( )
A.20° B.80° C.100° D.120°
【分析】由题意设∠AOB为x,∠BOC为3x,再根据角的平分线的性质得出∠BOD=12∠BOC=2x,于是得x+2x=60°,求得x,再求∠AOC的度数即可.
【解析】∵∠AOB:∠BOC=1:4,
∴设∠AOB为x,∠BOC为4x,
∵OD平分∠BOC,
∴∠BOD=12∠BOC=2x,
∵∠AOD=60°,
∴x+2x=60°,
∴x=20°,
4x=80°,
∴∠AOC=∠AOB+∠BOC=20°+80°=100°,
故选:C.
10.(2020•新华区一模)按图1~图4的步骤作图,下列结论错误的是( )
A.12∠AOB=∠AOP B.∠AOP=∠BOP
C.2∠BOP=∠AOB D.∠BOP=2∠AOP
【分析】根据角平分线的定义对各选项进行逐一分析即可.
【解析】∵OP是∠AOB的平分线,
∴∠AOB=2∠AOP=2∠BOP,
∠AOP=∠BOP=12∠AOB,
∴选项A、B、C均正确,选项D错误.
故选:D.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋•宝安区期末)60°36′= 60.6 度.
【分析】依据度分秒的换算即可得到结果.
【解析】36′=0.6°,
∴60°36′=60.6°,
故答案为:60.6.
12.(2019秋•顺城区期末)点A、B、C是同一直线上的三个点,若AB=8cm,BC=3cm,则AC= 11或5 cm.
【分析】分点B在点A、C之间和点C在点A、B之间两种情况讨论.
【解析】(1)点B在点A、C之间时,AC=AB+BC=8+3=11cm;
(2)点C在点A、B之间时,AC=AB﹣BC=8﹣3﹣5cm.
∴AC的长度为11cm或5cm.
13.(2019秋•石景山区期末)如图,①~④展开图中,能围成三棱柱的是 ② .
【分析】依据展开图的特征,即可得到围成的几何体的类型.
【解析】图①能围成圆锥;图②能围成三棱柱;图③能围成正方体;图④能围成四棱锥;
故答案为:②.
14.(2019秋•青川县期末)如图所示,两个直角三角形的直角顶点重合,如果∠AOD=118°,那么∠BOC= 62° .
【分析】根据题意得到∠AOB=∠COD=90°,再计算∠BOD=∠AOD﹣90°=28°,然后根据∠BOC=∠COD﹣∠BOD进行计算即可.
【解析】∵∠AOB=∠COD=90°,
而∠AOD=118°,
∴∠BOD=∠AOD﹣90°=28°,
∴∠BOC=∠COD﹣∠BOD=90°﹣28°=62°.
故答案为:62°.
15.(2019秋•沈河区期末)已知线段MN=16cm,点P为任意一点,那么线段MP与NP和的最小值是 16 cm.
【分析】根据线段的性质解答即可.
【解析】如图所示:
所以线段MP与NP和的最小值是16cm,
故答案为;16
16.(2019秋•通州区期末)已知∠AOB=60°,以点O为端点作射线OC,使∠BOC=20°,再作∠AOC的平分线OD,则∠AOD的度数为 20°或40° .
【分析】考虑线段OC在角的内部和外部两种情况,每一种情况都用角的定义和角平分的定义求解,经计算结果为20°或40°.
【解析】(1)当OC在∠AOB的内部时,
如图1所示:
∵∠BOC=20°,∠AOB=60°,
∠AOB=∠AOC+∠BOC,
∴∠AOC=60°﹣20°=40°,
又∵OD是∠AOC的平分线,
∴∠AOD=∠COD=12∠AOC=20°;
(2)当OC在∠AOB的外部时,
如图2所示:
∵∠AOC=∠AOB+∠BOC,
∠AOB=60°,∠BOC=20°,
∴AOC=80°,
又∵OD是∠AOC的平分线,
∴∠AOD=∠COD=12∠AOC=40°;
综合所述∠AOD的度数有两个,
故答案为20°或40°.
17.(2019秋•茂名期中)某几何体从三个方向看到的图形分别如图,则该几何体的体积为 3π .
【分析】由主视图和俯视图可得此几何体为柱体,根据左视图是圆及圆心可判断出此几何体为圆柱.
【解析】由三视图可得,此几何体为圆柱,
所以圆柱的体积为3×π⋅(22)2=3π,
故答案为:3π
18.(2020春•宜春期末)如图,∠AOC=∠BOD=90°,∠AOB=70°,在∠AOB内画一条射线OP得到的图中有m对互余的角,其中∠AOP=x°,且满足0<x<50,则m= 3或4或6 .
【分析】分三种情况下:①∠AOP=35°,②∠AOP=20°,③0<x<50中的其余角,根据互余的定义找出图中互余的角即可求解.
【解析】①∠AOP=35°,互余的角有∠AOP与∠COP,∠BOP与∠COP,∠AOB与∠COB,∠COD与∠COB,一共4对;
②∠AOP=20°,互余的角有∠AOP与∠COP,∠AOP与∠AOB,∠AOP与∠COD,∠COD与∠COB,∠AOB与∠COB,∠COP与∠COB,一共6对;
③0<x<50中35°与20°的其余角,互余的角有∠AOP与∠COP,∠AOB与∠COB,∠COD与∠COB,一共3对.
则m=3或4或6.
故答案为:3或4或6.
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2019秋•长葛市期末)如图,已知A、B、C、D四点,根据下列要求画图:
(1)画直线AB、射线AD;
(2)画∠CDB;
(3)找一点P,使点P既在AC上又在BD上.
【分析】(1)利用直线以及射线的定义画出图形即可;
(2)利用角的定义作射线DC,DB即可;
(3)连接AC,BD即可得出P点.
【解析】(1)如图所示:直线AB、射线AD即为所求;
(2)如图所示:∠CDB即为所求;
(3)如图所示:点P即为所求.
20.(2020•江北区模拟)将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.
(1)以下两个方格图中的阴影部分能表示立方体表面展开图的是 A (填A或B).
(2)在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示)
(3)如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)
【分析】(1)有“田”字格的展开图都不能围成正方体,据此可排除B,从而得出答案;
(2)可利用“1、3、2”作图(答案不唯一);
(3)根据裁剪线裁剪,再展开.
【解析】(1)两个方格图中的阴影部分能表示立方体表面展开图的是A,
故答案为:A.
(2)立方体表面展开图如图所示:
(3)将其表面展开图画在方格图中如图所示:
21.已知∠1是∠2的2倍,∠1的余角的3倍与∠2的补角相等,求∠1、∠2的度数.
【分析】利用题中“∠1是∠2的2倍,∠1的余角的3倍与∠2的补角相等”作为相等关系列方程求解即可.
【解析】设∠2是x,则∠1=2x,
则3(90°﹣2x)=180°﹣x,
解得x=18°.
故∠1=36°,∠2=18°.
22.(2019秋•襄州区期末)已知:如图,AB=18cm,点M是线段AB的中点,点C把线段MB分成MC:CB=2:1的两部分,求线段AC的长.
请补充完成下列解答:
解:∵M是线段AB的中点,AB=18cm,
∴AM=MB= 12 AB= 9 cm.
∵MC:CB=2:1,
∴MC= 23 MB= 6 cm.
∴AC=AM+ MC = 9 + 6 = 15 cm.
【分析】根据线段中点的性质,可得AM,根据线段的比,可得MC,根据线段的和差,可得答案.
【解析】∵M是线段AB的中点,且AB=18cm,
∴AM=MB=12AB=9cm.
∵MC:CB=2:1,
∴MC=23MB=6cm.
∵AC=AM+MC,
∴AC=9+6=15cm,
故答案为:12,9,23,6,MC,9,6,15.
23.(2019秋•蒙城县期末)如图,O为直线AB上一点,OM是∠AOC的角平分线,ON是∠COB的平分线
(1)指出图中所有互为补角的角.
(2)求∠MON的度数.
(3)指出图中所有互为余角的角.
【分析】(1)根据如果两个角的和等于180°(平角),就说这两个角互为补角进行分析即可;
(2)根据角平分线定义求出∠COM=12∠AOC,∠CON=12∠BOC,求出∠MON=∠COM+∠CON=12(∠AOC+∠BOC),把∠AOC+∠BOC=180°代入求出即可;
(3)根据如果两个角的和等于90°(直角),就说这两个角互为余角进行分析即可.
【解析】(1)∠AOM与∠MOB,∠AOC与∠BOC,∠AON与∠BON,∠COM与∠MOB,∠CON与∠AON;
(2)∵∠AOC的平分线是OM,∠BOC的平分线是ON,
∴∠COM=12∠AOC,∠CON=12∠BOC,
∵∠AOB=∠AOC+∠BOC=180°,
∴∠MON=∠COM+∠CON
=12(∠AOC+∠BOC)
=12×180°
=90°,
(3)∠AOM与∠BON,∠COM与∠BON,∠CON与∠AOM,∠CON与∠COM.
24.(2019秋•鄄城县期末)如图,已知线段AB、a、b.
(1)请用尺规按下列要求作图:(不要求写作法,但要保留作图痕迹)
①延长线段AB到C,使BC=a;
②反向延长线段AB到D,使AD=b.
(2)在(1)的条件下,如果AB=8cm,a=6m,b=10cm,且点E为CD的中点,求线段AE的长度.
【分析】(1)根据题意画出图形即可;
(2)根据线段的画出和线段的中点的定义即可得到结论.
【解析】(1)①如图所示,线段BC即为所求,
②如图所示,线段AD即为所求;
(2)∵AB=8cm,a=6m,b=10cm,
∴CD=8+6+10=24cm,
∵点E为CD的中点,
∴DE=12DC=12cm,
∴AE=DE﹣AD=12﹣10=2cm.
25.(2019秋•琅琊区期末)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 北偏东70° ;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
【分析】(1)先求出∠AOB=55°,再求得∠NOC的度数,即可确定OC的方向;
(2)根据∠AOB=55°,∠AOC=∠AOB,得出∠BOC=110°,进而求出∠COD的度数;
(3)根据射线OE平分∠COD,即可求出∠COE=35°再利用∠AOC=55°求出答案即可.
【解析】(1)∵OB的方向是北偏西40°,OA的方向是北偏东15°,
∴∠NOB=40°,∠NOA=15°,
∴∠AOB=∠NOB+∠NOA=55°,
∵∠AOB=∠AOC,
∴∠AOC=55°,
∴∠NOC=∠NOA+∠AOC=70°,
∴OC的方向是北偏东70°;
故答案为:北偏东70°;
(2)∵∠AOB=55°,∠AOC=∠AOB,
∴∠BOC=110°.
又∵射线OD是OB的反向延长线,
∴∠BOD=180°.
∴∠COD=180°﹣110°=70°.
(3)∵∠COD=70°,OE平分∠COD,
∴∠COE=35°.
∵∠AOC=55°.
∴∠AOE=90°.
26.(2020春•南岗区期末)已知,在∠AOB内部作射线OC,OD平分∠BOC,∠AOD+∠COD=120°.
(1)如图1,求∠AOB的度数;
(2)如图2,在∠AOB的外部和∠BOD的内部分别作射线OE、OF,已知∠COD=2∠BOF+∠BOE,求证:OF平分∠DOE;
(3)如图3,在(2)的条件下,在∠COD内部作射线OM,当∠BOM=4∠COM,∠BOE=1110∠AOC时,求∠MOF的度数.
【分析】(1)根据OD平分∠BOC,得∠BOD=∠COD,再由∠AOD+∠COD=120°,得∠AOD+∠BOD=120°,即∠AOB=120°;
(2)根据OD平分∠BOC,得∠BOD=∠COD,再由∠COD=2∠BOF+∠BOE,得∠BOD=2∠BOF+∠BOE,可得∠DOF=∠BOD﹣∠BOF=2∠BOF+∠BOE﹣∠BOF=∠BOF+∠BOE=∠EOF,即可得出结论;
(3)设∠AOC=10α,则∠BOE=11α,由∠AOB=120°得∠BOC=∠AOB﹣∠AOC=120°﹣10α,根据OD平分∠BOC,得∠COD=∠BOD=12∠BOC=60°﹣5α,再由∠BOM=4∠COM,得∠COM=15∠BOC=15(120°﹣10α)=24°﹣2α,可得∠DOM=∠COD﹣∠COM=36°﹣3α,∠DOE=∠BOD+∠BOE=60°+6α,根据OF平分∠DOE可得∠DOF=12∠DOE=12(60°+6α)=30°+3α,由∠MOF=∠DOM+∠DOF可得结果.
【解答】(1)解:∵OD平分∠BOC,
∴∠BOD=∠COD,
∵∠AOD+∠COD=120°,
∴∠AOD+∠BOD=120°,
即∠AOB=120°;
(2)证明:∵OD平分∠BOC,
∴∠BOD=∠COD,
∵∠COD=2∠BOF+∠BOE,
∴∠BOD=2∠BOF+∠BOE,
∴∠DOF=∠BOD﹣∠BOF=2∠BOF+∠BOE﹣∠BOF=∠BOF+∠BOE=∠EOF,
∴OF平分∠DOE;
(3)解:设∠AOC=10α,则∠BOE=11α,
∵∠AOB=120°,
∴∠BOC=∠AOB﹣∠AOC=120°﹣10α,
∵OD平分∠BOC,
∴∠COD=∠BOD=12∠BOC=60°﹣5α,
∵∠BOM=4∠COM,
∴∠COM=15∠BOC=15(120°﹣10α)=24°﹣2α,
∴∠DOM=∠COD﹣∠COM=(60°﹣5α)﹣(24°﹣2α)=36°﹣3α,
∴∠DOE=∠BOD+∠BOE=(60°﹣5α)+11α=60°+6α,
∵OF平分∠DOE,
∴∠DOF=12∠DOE=12(60°+6α)=30°+3α,
∴∠MOF=∠DOM+∠DOF=(36°﹣3α)+(30°+3α)=66°.
相关资料
更多









