北京市东城区高考数学三年（2021-2023）模拟题知识点分类汇编-计数原理与概率统计

这是一份北京市东城区高考数学三年（2021-2023）模拟题知识点分类汇编-计数原理与概率统计，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
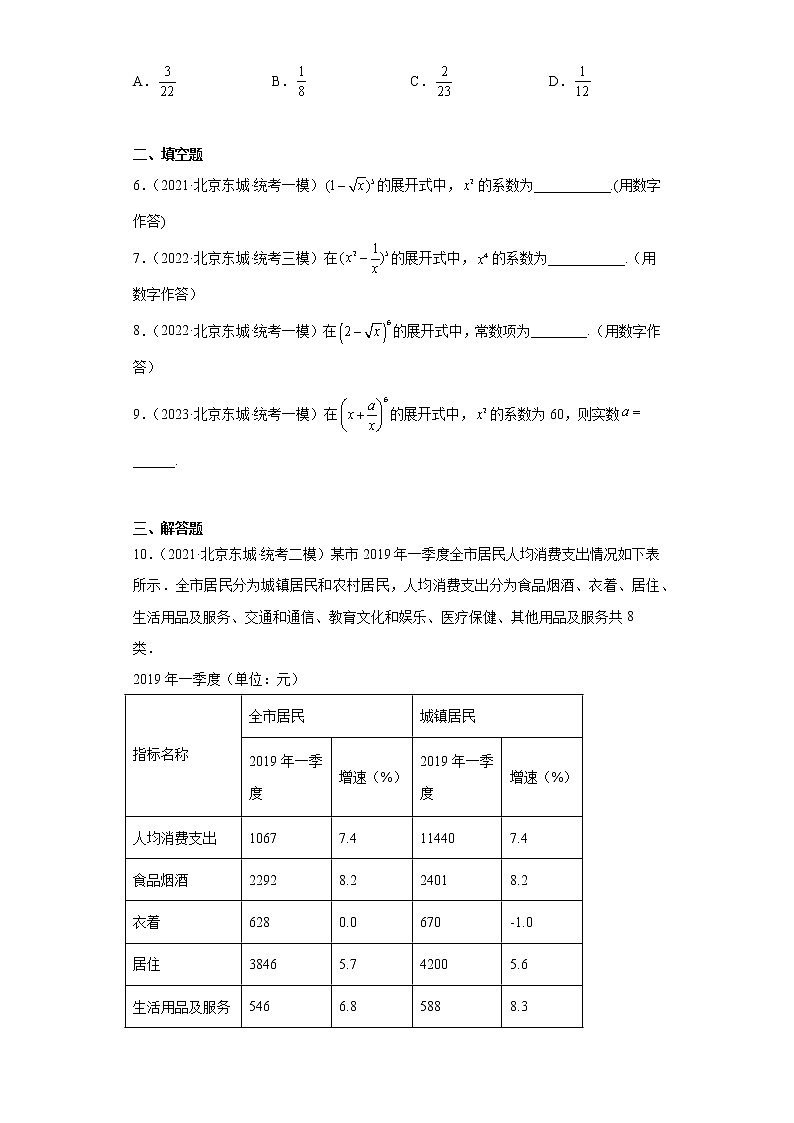
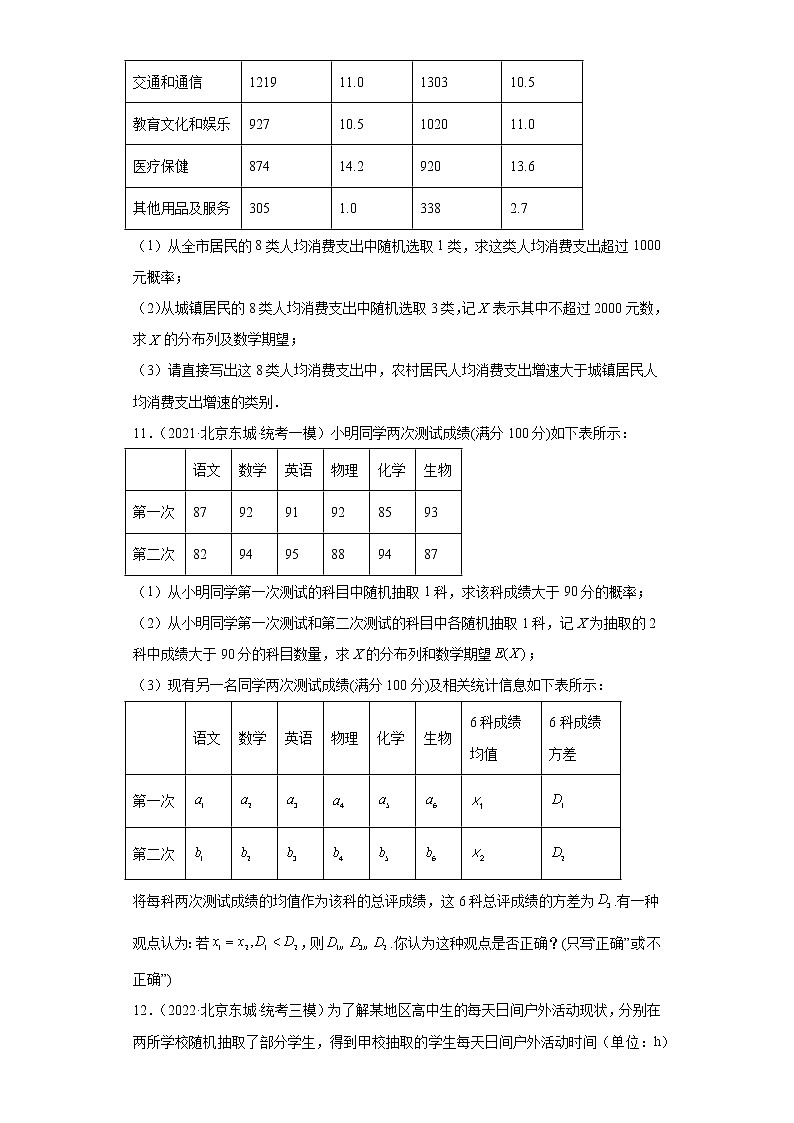
北京市东城区高考数学三年（2021-2023）模拟题知识点分类汇编-计数原理与概率统计 一、单选题1．（2021·北京东城·统考一模）某中学高一､高二和高三各年级人数见下表.采用分层抽样的方法调查学生的健康状况，在抽取的样本中，高二年级有20人，那么该样本中高三年级的人数为（    ）年级人数高一550高二500高三450合计1500 A．18 B．22 C．40 D．602．（2022·北京东城·统考三模）若某地区60岁及以上人群的新冠疫苗全程（两针）接种率为60%，加强免疫接种（第三针）的接种率为36%，则在该地区完成新冠疫苗全程接种的60岁及以上人群中随机抽取一人，此人完成了加强免疫接种的概率为（    ）A．0.6 B．0.375 C．0.36 D．0.2163．（2022·北京东城·统考二模）《周髀算经》中对圆周率有“径一而周三”的记载，已知两周率小数点后20位数字分别为14159  26535 89793  23846．若从这20个数字的前10个数字和后10个数字中各随机抽取一个数字，则这两个数字均为奇数的概率为（    ）A． B． C． D．4．（2022·北京东城·统考二模）在的展开式中，第4项的系数为（    ）A． B．80 C． D．105．（2022·北京东城·统考一模）在中国农历中，一年有24个节气，“立春”居首.北京2022年冬奥会开幕正逢立春，开幕式上“二十四节气”的倒计时让全世界领略了中华智慧.墩墩同学要从24个节气中随机选取3个介绍给外国的朋友，则这3个节气中含有“立春”的概率为（    ）A． B． C． D． 二、填空题6．（2021·北京东城·统考一模）的展开式中，的系数为___________.(用数字作答)7．（2022·北京东城·统考三模）在的展开式中，的系数为___________.（用数字作答）8．（2022·北京东城·统考一模）在的展开式中，常数项为________.（用数字作答）9．（2023·北京东城·统考一模）在的展开式中，的系数为60，则实数______. 三、解答题10．（2021·北京东城·统考二模）某市2019年一季度全市居民人均消费支出情况如下表所示．全市居民分为城镇居民和农村居民，人均消费支出分为食品烟酒、衣着、居住、生活用品及服务、交通和通信、教育文化和娱乐、医疗保健、其他用品及服务共8类．2019年一季度（单位：元）指标名称全市居民城镇居民2019年一季度增速（%）2019年一季度增速（%）人均消费支出10677.4114407.4食品烟酒22928.224018.2衣着6280.0670-1.0居住38465.742005.6生活用品及服务5466.85888.3交通和通信121911.0130310.5教育文化和娱乐92710.5102011.0医疗保健87414.292013.6其他用品及服务3051.03382.7（1）从全市居民的8类人均消费支出中随机选取1类，求这类人均消费支出超过1000元概率；（2）从城镇居民的8类人均消费支出中随机选取3类，记表示其中不超过2000元数，求的分布列及数学期望；（3）请直接写出这8类人均消费支出中，农村居民人均消费支出增速大于城镇居民人均消费支出增速的类别．11．（2021·北京东城·统考一模）小明同学两次测试成绩(满分100分)如下表所示： 语文数学英语物理化学生物第一次879291928593第二次829495889487（1）从小明同学第一次测试的科目中随机抽取1科，求该科成绩大于90分的概率；（2）从小明同学第一次测试和第二次测试的科目中各随机抽取1科，记X为抽取的2科中成绩大于90分的科目数量，求X的分布列和数学期望；（3）现有另一名同学两次测试成绩(满分100分)及相关统计信息如下表所示： 语文数学英语物理化学生物6科成绩均值6科成绩方差第一次第二次将每科两次测试成绩的均值作为该科的总评成绩，这6科总评成绩的方差为.有一种观点认为：若，则.你认为这种观点是否正确？(只写“正确”或“不正确”)12．（2022·北京东城·统考三模）为了解某地区高中生的每天日间户外活动现状，分别在两所学校随机抽取了部分学生，得到甲校抽取的学生每天日间户外活动时间（单位：h）的统计表和乙校抽取的学生每天日间户外活动时间（单位：h）的频率分布直方图如下.乙校抽取的学生每天日间户外活动时间频率分布直方图组别每天日间户外活动时间（单位：h）人数11202250360470甲校抽取的学生每天日间户外活动时间统计表(1)根据图表中的数据，估计甲校学生每天日间户外活动时间的25%分位数在第几组；(2)已知每天日间户外活动时间不低于2h可以对保护视力起到积极作用.现从乙校全体学生中随机选抽取2人，记其中每天日间户外活动时间不低于2h的人数为X，求X的分布列和数学期望；(3)根据上述数据，能否推断甲校抽取的学生每天日间户外活动时间的平均值一定低于乙校抽取的学生每天日间户外活动时间的平均值？说明理由.13．（2022·北京东城·统考二模）某部门为了解青少年视力发展状况，从全市体检数据中，随机抽取了名男生和名女生的视力数据．分别计算出男生和女生从小学一年级（年）到高中三年级（年）每年的视力平均值，如图所示．(1)从年到年中随机选取年，求该年男生的视力平均值高于上一年男生的视力平均值的概率；(2)从年到年这年中随机选取年，设其中恰有年女生的视力平均值不低于当年男生的视力平均值．求的分布列和数学期望：(3)由图判断，这名学生的视力平均值从哪年开始连续三年的方差最小？（结论不要求证明）14．（2022·北京东城·统考一模）根据Z市2020年人口普查的数据，在该市15岁及以上常住人口中，各种受教育程度人口所占比例（精确到0.01）如下表所示：受教育程度性别未上学小学初中高中大学专科大学本科硕士研究生博士研究生男0.000.030.140.110.070.110.030.01女0.010.040.110.110.080.120.030.00合计0.010.070.250.220.150.230.060.01(1)已知Z市15岁及以上常住人口在全市常住人口中所占比例约为85%，从全市常住人口中随机选取1人，试估计该市民年龄为15岁及以上且受教育程度为硕士研究生的概率；(2)从Z市15岁及以上常住人口中随机选取2人，记这2人中受教育程度为大学本科及以上的人数为X，求X的分布列和数学期望；(3)若受教育程度为未上学、小学、初中、高中、大学专科及以上的受教育年限分别记为0年、6年、9年、12年、16年，设Z市15岁及以上男性与女性常住人口的平均受教育年限分别为年和年，依据表中的数据直接写出与的大小关系.（结论不要求证明）15．（2023·北京东城·统考一模）甲、乙两名同学积极参与体育锻炼，对同一体育项目，在一段时间内甲进行了6次测试，乙进行了7次测试.每次测试满分均为100分，达到85分及以上为优秀.两位同学的测试成绩如下表：次数同学第一次第二次第三次第四次第五次第六次第七次甲807882869593—乙76818085899694(1)从甲、乙两名同学共进行的13次测试中随机选取一次，求该次测试成绩超过90分的概率；(2)从甲同学进行的6次测试中随机选取4次，设X表示这4次测试成绩达到优秀的次数，求X的分布列及数学期望EX；(3)从乙同学进行的7次测试中随机选取3次，设Y表示这3次测试成绩达到优秀的次数，试判断数学期望EY与（2）中EX的大小.（结论不要求证明）
参考答案：1．A【分析】根据分层抽样的概念及方法，列出方程，即可求解.【详解】设该样本中高三年级的人数为人，根据分层抽样的概念及方法，可得，解得人.故选：A.2．A【分析】设事件为抽取的一人完成新冠疫苗全程接种，事件为抽取的一人完成加强免疫接种，进而结合题意，根据条件概率公式求解即可.【详解】解：设事件为抽取的一人完成新冠疫苗全程接种，事件为抽取的一人完成加强免疫接种，所以，，所以在该地区完成新冠疫苗全程接种的60岁及以上人群中随机抽取一人，此人完成了加强免疫接种的概率为.故选：A3．D【分析】利用古典概型概率公式即得.【详解】因为从这20个数字的前10个数字中有7个奇数，后10个数字中有5个奇数，所以从这20个数字的前10个数字和后10个数字中各随机抽取一个数字，这两个数字均为奇数的概率为.故选：D.4．A【分析】先写出的展开式的通项公式，再令，即得.【详解】因为的展开式的通项公式为，令，则展开式中第4项的系数为，故选：A. 5．B【分析】利用古典概型运算公式进行求解即可.【详解】这3个节气中含有“立春”的概率为,故选：B6．5【分析】利用二项展开式的通项公式可求得结果.【详解】的展开式的通项公式为，，令，得，所以的系数为.故答案为：57．10【分析】在二项展开式的通项公式中，令的幂指数等于4，求出的值，即可求得展开式中的系数．【详解】的展开式的通项公式为，令，求得，故展开式中的系数为，故答案为：10．8．【分析】利用二项式的通项公式进行求解即可.【详解】二项式的通项公式为，令，所以常数项为，故答案为：9．【分析】求出二项展开式的通项，令的指数等于2，求得，再根据展开式中的系数为60，即可得出答案.【详解】的展开式的通项为，令，则，则在展开式中，的系数为，所以.故答案为：.10．（1）；（2）分布列见详解，；（3）答案见详解．【分析】（1）8类人均消费支出中有3类人均消费支出超过1000元，故概率可求；（2）列出变量的可能取值，结合超几何分布求解相应概率即可得分布列及数学期望；（3）根据表格数据即可得出结果．【详解】（1）8类人均消费支出中有3类人均消费支出超过1000元，故所求概率为；（2）依题意知的可能取值为1，2，3则 则的分布列为123；（3）农村居民人均消费支出增速大于城镇居民人均消费支出增速的类别有衣着，居住，交通和通信，医疗保健．【点睛】求离散型随机变量的分布列时，关键要判断随机变量是否服从二项分布或超几何分布等特殊的分布．11．（1）（2）分布列见解析，（3）不正确【分析】（1）根据古典概型的概率公式计算可得结果；（2）计算出的各个取值的概率可得分布列，根据期望公式计算可得数学期望；（3）根据方差公式计算，结合比较可得答案.【详解】（1）共有6科成绩，其中成绩大于90分的有数学、英语、物理和生物共4科，所以从小明同学第一次测试的科目中随机抽取1科，该科成绩大于90分的概率为.（2）的所有可能取值为：0，1，2，，，，所以X的分布列为：012数学期望.（3）设，则，则，同理可得，，因为，所以，所以的符号不确定，所以与无法比较大小，，所以，故这种观点不正确.【点睛】关键点点睛：掌握求离散型随机变量的分布列的步骤和数学期望公式是解题关键.12．(1)第2组(2)分布列答案见解析，数学期望：(3)不能，理由见解析 【分析】（1）利用图表中的数据结合25%分位计算判断；（2）根据题意可得，根据二项分布求分布列和期望；（3）用每组区间的中点值进行估计求平均数的估计值，用每组区间的左端点值进行估计求平均数最小值，计算判断．【详解】（1）根据表中数据，估计甲校学生每天日间户外活动时间25%分位数在第2组.（2）由频率分布直方图可知，乙校参与调查的学生每天日间户外活动时间不低于的频率为.由此估计乙校全体学生每天日间户外活动时间不低于的概率约为0.3.X的所有可能取值为0，1，2.，，，所以X的分布列为X012P0.490.420.09.（3）不能.若甲校参与调查的学生每组中的数据恰好都取区间中点值，则甲校参与调查的学生每天的日间户外活动时间的平均值.若乙校参与调查的学生每组中的数据恰好都取相应区间的左端点值，则乙校参与调查的学生每天的日间户外活动时间的平均值.此时，.13．(1)(2)分布列见解析；数学期望(3)自年开始的连续三年，名学生的视力平均值方差最小 【分析】（1）根据折线图可确定该年男生的视力平均值高于上一年男生的视力平均值的共有个，由此可计算得到概率；（2）由折线图知女生的视力平均值不低于当年男生的视力平均值的年份有个，根据超几何分布概率公式可确定每个取值对应的概率，由此可得分布列；根据数学期望计算公式可求得期望值；（3）根据折线图可确定自年开始的连续三年，学生视力波动程度最小，由此可得结论.【详解】（1）由折线图可知：从年到年中，该年男生的视力平均值高于上一年男生的视力平均值的共有个；所求概率.（2）从年到年这年中，女生的视力平均值不低于当年男生的视力平均值的年份有个；所有可能的取值为，；；；则的分布列为：的数学期望.（3）由折线图知：自年开始的连续三年视力平均值接近且连续三年数据相差不大，自年开始的连续三年，名学生的视力平均值波动幅度最小，则自年开始的连续三年，名学生的视力平均值方差最小.14．(1);(2)答案见解析；(3) 【分析】（1）结合概率乘法的计算公式即可求出结果；（2）求出X的可能取值，进而求出对应的概率，即可求出结果；（3）根据平均数的概念即可得出结论.【详解】（1）因为在该市15岁及以上常住人口中，受教育程度为硕士研究生的人口所占比例为0.06，则估计该市民年龄为15岁及以上且受教育程度为硕士研究生的概率85％；（2）该市15岁及以上常住人口中，受教育程度为大学本科及以上的人口所占比例为0.23+0.06+0.01=0.3，X的可能取值为0，1，2，则,,,故X的分布列为0120.490.420.09,（3）由题意，男性平均受教育年限为，女性平均受教育年限为，则.15．(1)(2)的分布列为所以.(3) 【分析】（1）根据表格中的数据，代入古典概型的概率计算公式即可求解；（2）根据题意先求出所有的可能取值，然后分别求出每一个值对应的概率，列出分布列并计算出期望即可求解；（3）根据题意先求出所有的可能取值，然后分别求出每一个值对应的概率，计算出期望与（2）中期望即可求解；【详解】（1）由题意可知：甲、乙两名同学共进行的13次测试中，测试成绩超过90分的共4次，由古典概型的概率计算公式可得，所以从甲、乙两名同学共进行的13次测试中随机选取一次，求该次测试成绩超过90分的概率.（2）由题意可知：从甲同学进行的6次测试中随机选取4次，这4次测试成绩达到优秀的次数的可能取值为1，2，3，则；；，所以的分布列为所以.（3）由题意可知：从乙同学进行的7次测试中随机选取3次，这3次测试成绩达到优秀的次数的可能取值为0，1，2，3，则；；；；所以的分布列为所以，.