沪科版八年级下册第18章 勾股定理18.1 勾股定理教学ppt课件

这是一份沪科版八年级下册第18章 勾股定理18.1 勾股定理教学ppt课件，共18页。PPT课件主要包含了知识要点，勾股定理的证明，SP+SQSR，几何语言，练一练，cm²，或100等内容，欢迎下载使用。
2.利用勾股定理进行计算
相传2 500年前，一次毕达哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系，同学们，我们也来观察下面的图案，看看你能发现什么？
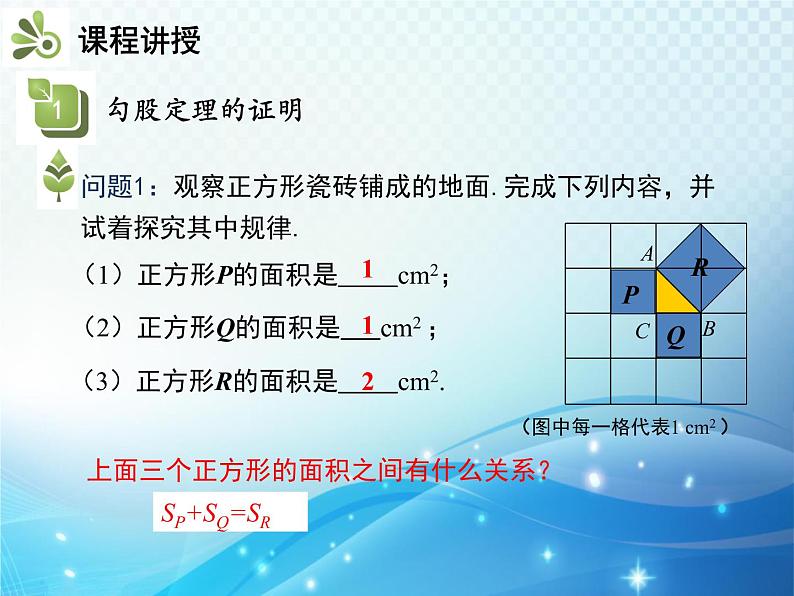
（图中每一格代表1 cm2 ）
（1）正方形P的面积是 cm2；
（2）正方形Q的面积是 cm2 ；
（3）正方形R的面积是 cm2.
上面三个正方形的面积之间有什么关系？
AC2+BC2=AB2
直角三角形ABC三边长度之间存在什么关系吗？
SP=AC2 SQ=BC2 SR=AB2
如果直角三角形的两条直角边长分别为a,b，斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
由上面的例子，我们猜想：
下面让我们跟着以前的数学家们用拼图法来证明这一猜想.
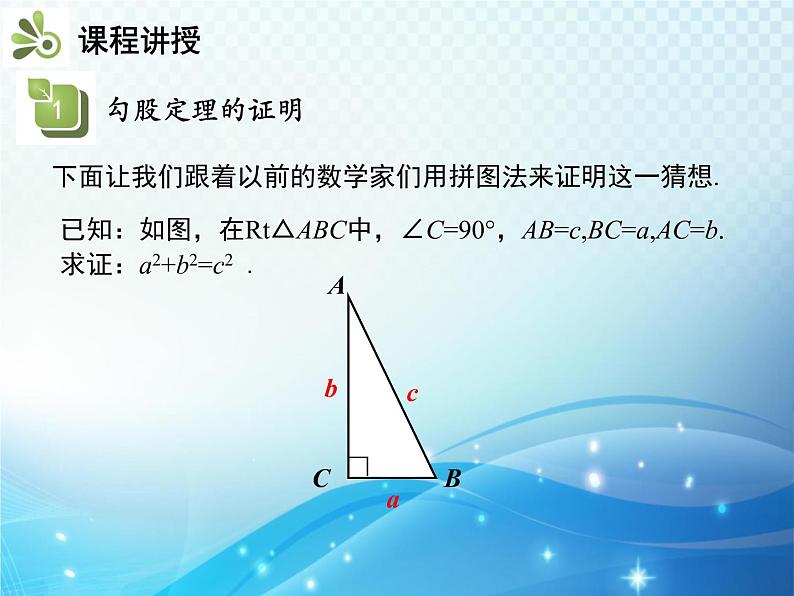
已知：如图，在Rt△ABC中，∠C=90°，AB=c,BC=a,AC=b.求证：a2+b2=c2 .
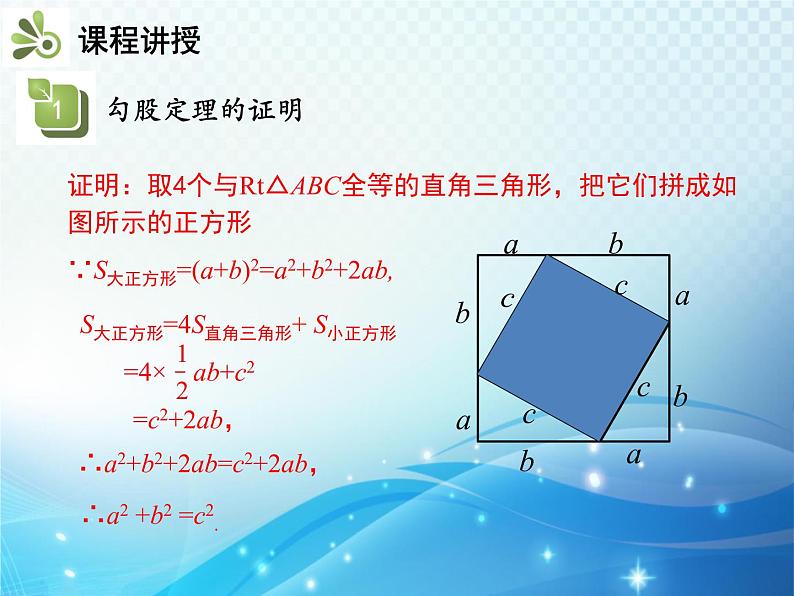
证明：取4个与Rt△ABC全等的直角三角形，把它们拼成如图所示的正方形
∴a2+b2+2ab=c2+2ab，
∴a2 +b2 =c2.
∵S大正方形=(a+b)2=a2+b2+2ab,
归纳：由前面的探索可以发现：对于任意的直角三角形，如果它的两条直角边分别为a，b，斜边为c，那么一定有a2+b2=c2.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.国外称为毕达哥拉斯定理.
∴a2+b2=c2（勾股定理）.
∵在Rt△ABC中 ，∠C=90°，
勾股定理揭示了直角三角形三边之间的关系.
例1 在Rt△ABC中，∠C＝90°，AB＝10 cm， BC＝8 cm，求AC的长． 解：由题意易知，AC2＋BC2＝AB2， 所以AC2＝AB2－BC2＝102－82＝36. 所以AC＝6 cm.
练一练：(中考·淮安)如图，在边长为1个单位长度的小正方形组成的网格中，点A，B都是格点，则线段AB的长度为(　　) A．5 B．6 C．7 D．25
例2 已知：如图，在Rt△ABC中,两直角边 AC=5,BC=12.求斜边上的高CD的长.
解：在Rt△ABC中， AB2=AC2+BC2=52+122=169 即 AB= =13.又∵Rt△ABC的面积， S△ABC = AC×BC= AB×CD. ∴ CD= .
如图，直线l上有三个正方形a，b，c，若a，c的 面积分别为3和4，则b的面积为(　　) A．16 B．12 C．9 D．7
归纳：由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积，它常与勾股定理联合使用．当直角三角形中所给的两条边没有指明是斜边或直角边时，其中一较长边可能是直角边，也可能是斜边，这种情况下一定要进行分类讨论，否则容易丢解.
1.图中阴影部分是一个正方形，则此正方形的面积为 _________.
2.在△ABC中, ∠C=90°,AC=6,CB=8,则△ABC面积为_____,斜边为上的高为______.
3.在△ABC中，∠C=90°.（1）若a=15，b=8，则c= . （2）若c=13，b=12，则a= .4.若直角三角形中，有两边长是6和8，则第三边长的平方为_________.