2023年中考数学二轮专项练习：二次函数压轴题（特殊四边形问题）

这是一份2023年中考数学二轮专项练习：二次函数压轴题（特殊四边形问题），共12页。试卷主要包含了解答题等内容，欢迎下载使用。
一、解答题
1．如图，抛物线与x轴交于A、B两点，与y轴交于点，顶点为D，且．
(1)求抛物线的解析式；
(2)若在线段上存在一点M，过点O作交的延长线于H，且，求点M的坐标；
(3)点P是y轴上一动点，点Q是在对称轴上一动点，是否存在点P，Q，使得以点P，Q，C，D为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由．
2．如图，抛物线与轴相交于点、点，与轴相交于点．
(1)请直接写出点，，的坐标；
(2)若点是抛物线段上的一点，当的面积最大时求出点的坐标，并求出面积的最大值．
(3)点是抛物线上的动点，作交轴于点，是否存在点，使得以、、、为顶点的四边形是平行四边形？若存在，请写出所有符合条件的点的坐标；若不存在，请说明理由．
3．如图，是将抛物线平移后得到的抛物线，其对称轴为，与轴的一个交点为，另一交点为，与轴交点为．
（1）求抛物线的函数表达式；
（2）若点为抛物线上一点，且，求点的坐标；
（3）点是抛物线上一点，点是一次函数的图象上一点，若四边形为平行四边形，这样的点是否存在？若存在，分别求出点的坐标，若不存在，说明理由．
4．如图，在平面直角坐标系中，二次函数y＝x2+bx+c的图象与x轴交于点A(﹣1，0)，B(3，0)，与y轴交于点C．
(1)b＝______，c＝______；
(2)若点D为第四象限内抛物线上的一个动点，过点D作DE∥y轴交BC于点E，过点D作DF⊥BC于点F，过点F作FG⊥y轴于点G，求出DE+FG的最大值及此时点D的坐标；
(3)若点P是该抛物线对称轴上的一点，点Q为坐标平面内一点，那么在抛物线上且位于x轴上方是否存在点M，使四边形OMPQ为正方形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
5．将抛物线向左平移1个单位，再向上平移4个单位后，得到抛物线．抛物线与轴交于点，，与轴交于点．已知，点是抛物线上的一个动点．
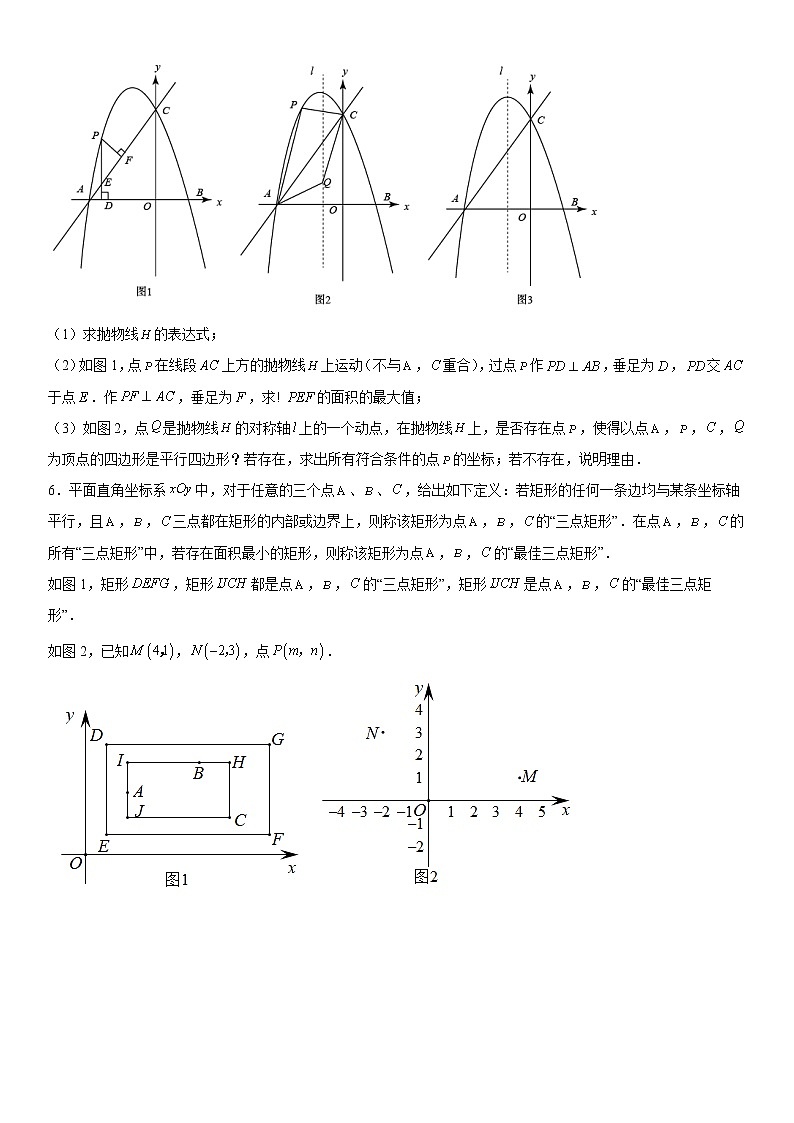
（1）求抛物线的表达式；
（2）如图1，点在线段上方的抛物线上运动（不与，重合），过点作，垂足为，交于点．作，垂足为，求的面积的最大值；
（3）如图2，点是抛物线的对称轴上的一个动点，在抛物线上，是否存在点，使得以点，，，为顶点的四边形是平行四边形？若存在，求出所有符合条件的点的坐标；若不存在，说明理由．
6．平面直角坐标系中，对于任意的三个点、、，给出如下定义：若矩形的任何一条边均与某条坐标轴平行，且，，三点都在矩形的内部或边界上，则称该矩形为点，，的“三点矩形”．在点，，的所有“三点矩形”中，若存在面积最小的矩形，则称该矩形为点，，的“最佳三点矩形”．
如图1，矩形，矩形都是点，，的“三点矩形”，矩形是点，，的“最佳三点矩形”．
如图2，已知，，点．
(1)①若，，则点，，的“最佳三点矩形”的周长为_________，面积为_________；
②若，点，，的“最佳三点矩形”的面积为24，求的值；
(2)若点在直线上．
①求点，，的“最佳三点矩形”面积的最小值及此时的取值范围；
②当点，，的“最佳三点矩形”为正方形时，求点的坐标；
(3)若点在抛物线上，当且仅当点，，的“最佳三点矩形”面积为18时，或，直接写出抛物线的解析式．
7．综合与探究
如图，抛物线经过点，两点，与y轴交于点C，且，点D是抛物线上第一象限内的一个动点，设点D的横坐标为m．连接．
(1)求抛物线的函数表达式；
(2)过点D作与y轴的平行线的直线l，与交于点E，当是以为底边的等腰三角形时，求点D的坐标．
(3)若点M是y轴上的动点，在坐标平面内是否存在点N，使以点A、C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．
8．如图，在平面直角坐标系中，已知抛物线y＝﹣x2＋x＋2与x轴相交于A，B两点，与y轴交于点C．
(1)求B、C两点的坐标；
(2)点P为直线BC上方抛物线上的任意一点，过P作PF∥x轴交直线BC于点F，过P作PE∥y轴交直线BC于点E，求线段EF的最大值及此时P点坐标；
(3)将该抛物线沿着射线AC方向平移个单位得到新抛物线y′，N是新抛物线对称轴上一点，在平面直角坐标系中是否存在点Q，使以点B、C、Q、N为顶点的四边形为菱形，若存在，请直接写出点Q点的坐标；若不存在，请说明理由．
9．如图，直线y=−x+4与x轴交于点A，与y轴交于点B，抛物线y=ax2−5x+c经过A、B、C三点，D为y轴上一动点，过点D作y轴的垂线与直线AB交于点E，与抛物线交于点F、G两点（F在G的左侧）．
(1)求抛物线的解析式及点C的坐标；
(2)在点D运动的过程中，若O、C、E、F为顶点的四边形是平行四边形，试求点D的坐标；
(3)如图2，当点D运动到点B上时（即B与D重合），有一点M在线段AB的上方且∠AMB=135°，连接MG，请直接写出线段MG的最小值．
10．已知二次函数y=x2﹣（a﹣1）x+a﹣2，其中a是常数．
（1）求证：不论a为何值，该二次函数的图象与x轴一定有公共点；
（2）当a=4时，该二次函数的图象顶点为A，与x轴交于B，D两点，与y轴交于C点，求四边形ABCD的面积．
11．将抛物线C1：y=﹣x2+沿x轴翻折，得到抛物线C2，如图所示
（1）请直接写出抛物线C2的解析式
（2）现将抛物线C1向左平移m个单位长度，平移后得到新抛物线的顶点为M，与x轴的交点从左到右依次为A、B；将抛物线C2向右也平移m个单位长度，平移后得到新抛物线的顶点为N，与x轴的交点从左到右依次为D、E．
①当B、D是线段AE的三等分点时，求m的值；
②在平移过程中，是否存在以点A、N、E、M为顶点的四边形是矩形的情形？若存在，请求出此时m的值；若不存在，请说明理由
12．如图，二次函数y＝ax2＋bx＋c的图象与x轴相交于点A（﹣1，0）、B（3，0）两点，与y轴相交于点C（0，﹣3）．
(1)求此二次函数的解析式；
(2)若抛物线的顶点为D，点E在抛物线上，且与点C关于抛物线的对称轴对称，直线AE交对称轴于点F，试判断四边形CDEF的形状，并证明你的结论．
13．已知抛物线交轴于点A，在的左侧），交轴于点．
(1)求点A的坐标；
(2)若经过点A的直线交抛物线于点．
①当且时交线段于，交轴于点，求的最大值；
②当且时，设为抛物线对称轴上一动点，点是抛物线上的动点，那么以A，，，为顶点的四边形能否成为矩形？若能，求出点的坐标，若不能，请说明理由．
14．如图，已知抛物线（a≠0）的图象的顶点坐标是（2，1），并且经过点（4，2），直线与抛物线交于B，D两点，以BD为直径作圆，圆心为点C，圆C与直线m交于对称轴右侧的点M（t，1），直线m上每一点的纵坐标都等于1．
（1）求抛物线的解析式；
（2）证明：圆C与x轴相切；
（3）过点B作BE⊥m，垂足为E，再过点D作DF⊥m，垂足为F，求MF的值．
15．如图，抛物线y＝ax2+bx+6经过点A（﹣2，0），B（4，0）两点，与y轴交于点C，设点D的横坐标为m（1＜m＜4）．连接AC、BC、DB、DC．
(1)求抛物线的函数表达式；
(2)当△BCD的面积等于△AOC的面积时，求m的值；
(3)当m＝3时，若点M是x轴正半轴上的一个动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B、D、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标，若不存在，请说明理由．
16．综合与探究
如图1，抛物线与x轴交于A，C两点，与y轴交于点B，顶点为点D．连接AB，BC．将沿x轴向右平移m个单位长度得到，线段与线段BC交于点E．
(1)求直线CD的函数表达式；
(2)当点E是的三等分点时，求m的值；
(3)如图2，当时，线段与CD交于点F，连接EF，．判断点F关于直线的对称点是否在抛物线上，并说明理由．
17．如图，抛物线y＝﹣x2+bx+c过等腰Rt△OAB的A，B两点，点B在点A的右侧，直角顶点A（0，3）．
（1）求抛物线的表达式．
（2）P是AB上方抛物线上的一点，作PQ⊥AB交OB于点Q，连接AP，是否存在点P，使四边形APQO是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由．
参考答案：
1．(1)
(2)
(3)或或
2．(1)，，
(2)点的坐标为时，有最大值
(3)存在，点的坐标为或或
3．（1）y=﹣x2+2x+3（2）（1，4）（3）P、Q的坐标是（0，3），（1，3）或（，）、（，）
4．(1)﹣2，3
(2)GF+DE有最大值，D
(3)存在，M点的坐标为或
5．（1）；（2）的面积最大值为；（3）点的坐标为或或．
6．(1)①18，18．②n=-1或5
(2)①12，1≤m≤2；②点P的坐标为（-1，7）或（4，-3）
(3)抛物线的解析式或
7．(1)
(2)
(3)，，，
8．(1)点B坐标为（4，0）；点C坐标为（0，2）．
(2)当m＝2时，EF有最大值，此时点P坐标为（2，3）．
(3)存在，点Q坐标为（﹣2，6）或（﹣2，﹣2）或（6，4）或（6，﹣4）．
9．(1)抛物线的解析式为y=x2−5x+4，点C的坐标为(1，0)；
(2)点D的坐标为(0，1+)或(0，3+)；
(3)线段MG的最小值为()．
10．（1）证明；（2）S四边形ABCD =．
11．（1）（2）①或；②是矩形，
12．(1)y＝x2﹣2x﹣3
(2)正方形
13．(1)
(2)①；②P点坐标为或．
14．（1） ；（2）11；（3） ．
15．(1)
(2)m的值为2
(3)存在， M点的坐标为或或
16．(1)
(2)或
(3)点在抛物线上
17．（1）y＝﹣x2+3x+3；（2）存在，当P（2，5）时，四边形APQO是平行四边形．