空间向量与立体几何-浙江省嘉兴市高考数学三年（2021-2023）模拟题知识点分类汇编

这是一份空间向量与立体几何-浙江省嘉兴市高考数学三年（2021-2023）模拟题知识点分类汇编，共37页。试卷主要包含了单选题，多选题，填空题，双空题，解答题等内容，欢迎下载使用。
空间向量与立体几何-浙江省嘉兴市高考数学三年（2021-2023）模拟题知识点分类汇编

一、单选题
1．（2023·浙江嘉兴·统考二模）已知正方体的棱长为为空间内一点且满足平面，过作与平行的平面，与交于点，则（    ）
A．1 B． C． D．
2．（2023·浙江嘉兴·统考模拟预测）《九章算术·商功》中记载：“斜解立方，得两堑堵.斜解堑堵，其一为阳马，一为鳖臑，不易之率也.”我们可以翻译为：取一长方体，分成两个一模一样的直三棱柱，称为堑堵.再沿堑堵的一顶点与相对的棱剖开，得一个四棱锥和一个三棱锥，这个四棱锥称为阳马，这个三棱锥称为鳖臑.现已知某个鳖臑的体积是1，则原长方体的体积是（    ）
A．8 B．6 C．4 D．3
3．（2022·浙江嘉兴·模拟预测）某几何体的三视图如图所示（单位：），则该几何体的体积（单位：）是（    ）

A． B． C． D．
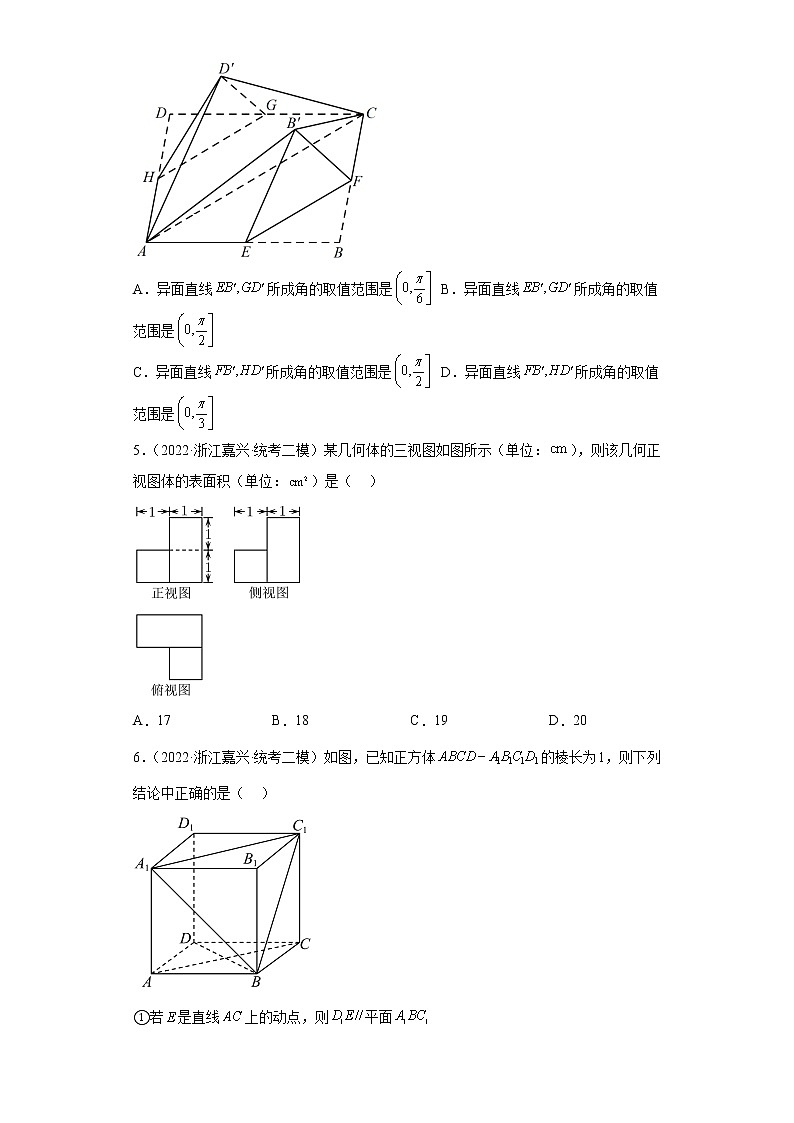
4．（2022·浙江嘉兴·模拟预测）如图，在矩形中，，E，F，G，H分别为边的中点，将分别沿直线翻折形成四棱锥，下列说法正确的是（    ）

A．异面直线所成角的取值范围是 B．异面直线所成角的取值范围是
C．异面直线所成角的取值范围是 D．异面直线所成角的取值范围是
5．（2022·浙江嘉兴·统考二模）某几何体的三视图如图所示（单位：），则该几何正视图体的表面积（单位：）是（    ）

A．17 B．18 C．19 D．20
6．（2022·浙江嘉兴·统考二模）如图，已知正方体的棱长为，则下列结论中正确的是（    ）

①若是直线上的动点，则平面
②若是直线上的动点，则三棱锥的体积为定值
③平面与平面所成的锐二面角的大小为
④若是直线上的动点，则
A．①②③ B．②③④ C．①②④ D．①③④
7．（2021·浙江嘉兴·统考模拟预测）某几何体的三视图如图所示（单位：），则该几何体的体积(单位：)是（    ）

A． B． C． D．
8．（2021·浙江嘉兴·统考模拟预测）某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（ ）

A．2 B．
C． D．
9．（2021·浙江嘉兴·统考模拟预测）如图，正方体中，是的中点，则（ ）

A．直线与直线相交，直线平面
B．直线与直线平行，直线//平面
C．直线与直线垂直，直线//平面
D．直线与直线异面，直线平面
10．（2021·浙江嘉兴·统考模拟预测）已知空间中两平面，直线，则“”是“”的（    ）
A．充分而不必要条件
B．必要而不充分条件
C．充要条件
D．既不充分也不必要条件
11．（2021·浙江嘉兴·统考二模）如图，矩形中，已知，，为的中点． 将沿着向上翻折至，记锐二面角的平面角为，与平面所成的角为，则下列结论不可能成立的是（    ）

A． B．
C． D．
12．（2021·浙江嘉兴·统考二模）某几何体（包含四棱锥）的三视图如图所示（单位：），则该几何体的体积（单位：）是（    ）

A． B． C． D．
13．（2021·浙江嘉兴·统考二模）已知空间中不过同一点的两条直线，及平面，则“，与平面所成的角相同”是“”的（    ）．
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
14．（2021·浙江嘉兴·统考二模）某几何体的三视图（单位：cm）如图所示，则该几何体中长度为3cm的棱有（    ）．

A．0条 B．1条 C．2条 D．3条

二、多选题
15．（2023·浙江嘉兴·统考二模）已知菱形的边长为，将沿对角线翻折，得到三棱锥，则在翻折过程中，下列说法正确的是（    ）
A．存在某个位置，使得
B．直线与平面所成角的最大值为
C．当二面角为时，三棱锥的外接球的表面积为
D．当时，分别以为球心，2为半径作球，这四个球的公共部分称为勒洛四面体，则该勒洛四面体的内切球的半径为
16．（2023·浙江嘉兴·统考模拟预测）已知正方体的棱长为2，，分别为，的中点，且与正方体的内切球（为球心）交于，两点，则下列说法正确的是（    ）
A．线段的长为
B．过，，三点的平面截正方体所得的截面面积为
C．三棱锥的体积为
D．设为球上任意一点，则与所成角的范围是

三、填空题
17．（2021·浙江嘉兴·统考模拟预测）三棱锥P-ABC中，PA，PB，PC两两垂直，，点Q为平面ABC内的动点，且满足，记直线PQ与直线AB的所成角为，则的取值范围为___________.

四、双空题
18．（2021·浙江嘉兴·统考二模）已知圆台的体积为cm3，母线长为3cm，高为cm，则圆台的侧面展开图（扇环）的圆心角的大小为______，它的侧面积为______cm2．

五、解答题
19．（2023·浙江嘉兴·统考二模）如图，在三棱台中，.

(1)求证：平面平面；
(2)若四面体的体积为2，求二面角的余弦值.
20．（2023·浙江嘉兴·统考模拟预测）如图在三棱柱中，为的中点，，.

(1)证明：；
(2)若，且满足：______，______（待选条件）.
从下面给出的①②③中选择两个填入待选条件，求二面角的正弦值.
①三棱柱的体积为；
②直线与平面所成的角的正弦值为；
③二面角的大小为60°；
注：若选择不同的组合分别解答，则按第一个解答计分.
21．（2022·浙江嘉兴·模拟预测）如图，四棱锥中，平面，平面,，F，M，N分别为的中点．

(1)求证：∥平面；
(2)求直线与平面所成角的正弦值．
22．（2022·浙江嘉兴·统考二模）如图，在四棱锥中，底面是等腰梯形，，，且.

(1)证明：；
(2)若E为中点，求直线与平面所成角的正弦值.
23．（2021·浙江嘉兴·统考模拟预测）如图，在三棱锥中，底面是边长2的等边三角形，，点F在线段BC上，且，为的中点，为的中点.

(Ⅰ)求证：//平面；
(Ⅱ)若二面角的平面角的大小为，求直线与平面所成角的正弦值.
24．（2021·浙江嘉兴·统考模拟预测）在四棱锥中，底面ABCD为平行四边形，平面平面，.

（1）证明：；
（2）求直线AP与平面PCD所成角的正弦值.
25．（2021·浙江嘉兴·统考二模）如图，四棱柱中，底面是矩形，，，，且二面角的平面角的大小为60°，，分别为，的中点．

（Ⅰ）求证：；
（Ⅱ）求与平面所成角的正弦值．
26．（2021·浙江嘉兴·统考二模）如图，在三棱柱中，，，是的中点，点在平面上的射影为的中点．

（Ⅰ）证明：平面；
（Ⅱ）若直线与平面所成角的正弦值为，求二面角的平面角的正切值．

参考答案：
1．D
【分析】由题意知平面平面，可先令为中点，再证明当点为中点时，满足平面平面，即可轻易得出的值.
【详解】因为为空间内一点且满足平面，过作与平行的平面，与交于点，
所以∥平面,而平面，故平面平面.
在正方体中，如图所示，取中点为,中点为,连接，
假设为中点，则为等腰三角形，中点为,所以;
又因为,,所以，
中点为,中点为,所以,而,所以，，平面，
所以平面，平面,所以；
因为，，,平面，
所以平面，平面，所以平面平面，符合题意，
故为中点，.
故选：D.

2．B
【分析】根据柱体和锥体体积公式求得正确答案.
【详解】如图所示，原长方体，
设矩形的面积为，，
鳖臑的体积为，
即，所以，
即原长方体的体积是.
故选：B

3．D
【分析】根据三视图还原原几何体的直观图，可知该几何体为四棱锥，结合图中数据可计算得出该几何体的体积.
【详解】根据三视图还原原几何体的直观图如下图所示：

由图可知，该几何体为四棱锥，且底面为直角梯形，四棱锥的高为，
结合图中的数据可知，该四棱锥的体积为.
故选：D.
4．C
【分析】建立空间直角坐标系，利用空间向量法求出异面直线所成角的余弦值，即可判断；
【详解】解：建立如图所示空间直角坐标系，由题意得，

和在平面中的投影分别在和上（如下图所示），

因为，令，则，
由比值可知，的x，y，z坐标比值为，所以令坐标为，
因为在平面中的投影在上，所以，
同理可得坐标为，
，
则，
解得，因为和的范围均为，
所以，即夹角范围是，故A，B错误；
同理可得，因为异面直线所成角范围是，则夹角范围是．即C正确，D错误；
故选：C．
5．B
【分析】先由三视图复原出几何体，再计算表面积即可.
【详解】由三视图可知该几何体为两个长方体拼接在一起，如图所示：

故表面积为：.
故选：B.
6．C
【分析】连接，利用面面平行的判定可证得平面平面，由面面平行性质可知①正确；根据①中结论，利用体积桥的方式，由可知②正确；由面面平行知平面与平面所成的锐二面角即为平面与平面所成的锐二面角，根据二面角平面角定义知所求角为，利用正切值可说明③错误；根据线面垂直的判定可证得平面，根据线面垂直性质知④正确.
【详解】对于①，连接，

，，四边形为平行四边形，，
又平面，平面，平面，
同理可得：平面，
，平面，平面平面，
若是直线上的动点，则平面，平面，①正确；

对于②，由①知，平面，
，②正确；
对于③，连接，交于点，连接，

平面平面，平面与平面所成的锐二面角即为平面与平面所成的锐二面角，
四边形为正方形，，为中点，
又，，
即为平面与平面所成的锐二面角的平面角，
，，
即平面与平面所成的锐二面角不为，③错误；
对于④，四边形为正方形，，
平面，平面，，
又，平面，平面；

若是直线上的动点，则平面，，④正确.
故选：C.
7．A
【分析】由三视图还原几何体，可知该几何体为一个三棱柱与一个三棱锥的组合体，从而即可求解该几何体的体积.
【详解】解：由三视图还原几何体，如图所示，可知该几何体为一个三棱柱与一个三棱锥的组合体，

所以体积，
故选：A.
8．A
【分析】由三视图得到直观图，再根据棱柱的体积公式计算可得；
【详解】解：依题意可得直观图如下所示：

所以
故选：A
9．C
【分析】建立空间直角坐标系，利用空间向量法证明平行与垂直，即可判断；
【详解】解：如图建立空间直角坐标系，令正方体的棱长为，则，，，，，，，，，所以，，，所以与不平行，故直线与直线不平行，即B错误；
，所以，所以，设面的法向量为，即，令，则，，所以，所以，因为平面，所以平面，故C正确；
因为，，故与不垂直，故D错误；
因为，，所以与不相交，故A错误；
故选：C

10．A
【分析】由已知条件判断空间线面、面面关系，根据推出关系判断条件的充分、必要性即可.
【详解】且，知：；而且，则与平面的关系可能有、、，
∴“”是“”的充分不必要条件.
故选：A
11．D
【分析】先取中点为，判断四边形是正方形，再作于，证明，，分别再直角三角形中计算和，比较即判断A正确；将选项A的结论平方，结合二倍角公式和余弦函数的单调性，即判断C正确；计算即判断B可能成立；判断，结合，即得，判断D错误.
【详解】记中点为，连接，连接与交于点， 依题意知四边形是正方形.

，故锐二面角的平面角为，
平面，过作于，则，
而相交于平面内，
故平面，故连接，则与平面所成的角为.
记，因为中，，
中，，所以①，选项A成立；
将①平方得：，所以，，
易见，都是锐角，则，∴，而，
根据余弦函数的单调性可知，，选项C成立；
因为，，若使，则需，
即当，可以成立，即B可能成立；
另外，由，都是锐角，且知，，知.
由选项C知，∴，选项D错误．
故选：D.
【点睛】关键点点睛：
本题的解题关键在于熟知二面角和线面角的定义，并准确找出，，才能结合三角函数及恒等变换等知识来突破难点.
12．A
【分析】利用三视图画出直观图可得几何体的体积．
【详解】由三视图可知，该几何体是下面为棱长等于的正方体，
上面是与正方体同底有一侧棱与底面垂直且高的四棱锥的组合体，
如下图，所以几何体的体积为：．

故选：A.
13．B
【分析】根据线面关系及其性质，直接判断即可得解.
【详解】如图，
当，与平面所成的角相同，，
而此时不共平行，故不成立，
反之，则，与平面所成的角相同成立，
故选：B.
14．C
【分析】由三视图求得直观图，在边长为2的正方体中画出该图形，分别求出各边长，即可得解.
【详解】
如图，在边长为2的正方体中画出其直观图为三棱锥，
其中为所在棱中点，
其中，
而，，
故选：C.
15．BCD
【分析】画出简图，数形结合，通过对几何体的观察、作辅助线、空间想象、计算等方式分别判断各选项，从而得出结论。
【详解】为等腰三角形，所以不可能是直角，选项错误；
如图，直线和夹角为，平面平面=，菱形,所以,当平面平面时，为直线与平面的平面角，此时直线与平面所成角为最大角，为，选项正确；
为二面角的平面角，设三棱锥的外接球的球心为，半径为，的外心为，则平分，，所以，三棱锥表面积为，选项正确；
设正四面体的外接球球心为，半径为，勒洛四面体的内切球的半径为，则

故，即，解得，由勒洛四面体的对称性可知，内切球切在每一个球面的中心，而顶点到切点的距离为2，故，选项D正确.
故答案为：BCD.

【点睛】关键点睛：解决与球有关的内切或外接问题时，关键是确定球心的位置，再利用球的截面小圆性质求解.
16．BC
【分析】过，，三点的截面为正六边形，球心为其中心，作出图形在正六边形中求出判断A，求出正六边形面积判断B，由等体积法求出三棱锥体积判断C，分析与所成角的最大最小值判断D.
【详解】过，，三点的截面为正六边形，球心为其中心，如图，

在正六边形中，，点到的距离为，，
所以，故A错误；
正六边形的面积，故B正确；，故C正确；
、、为球的切线，故当为中点时，与所成角最小为0，
，所以，
当与球相切且P在平面OAC内时，与所成角最大为，故D错误.
故选：BC.
17．
【分析】根据已知条件先确定出在平面内的轨迹，然后通过建立空间直角坐标系，根据两直线方向向量夹角的余弦值结合三角函数值的范围，计算出两直线所成角的正弦值的取值范围.
【详解】因为两两垂直，且，所以由全等三角形可知，
所以三棱锥为正三棱锥，记在底面内的投影为，
所以，
因为，所以，所以，
因为，所以，所以的轨迹是以为圆心半径为的圆，
取中点，连接，可知经过点，建立如下图所示的空间直角坐标系：

设，，
所以，
所以，
所以，
所以，且，
所以，所以，
故答案为：.
【点睛】思路点睛：异面直线所成角的余弦值的向量求法：
（1）先分别求解出两条异面直线的一个方向向量；
（2）计算出两个方向向量夹角的余弦值；
（3）根据方向向量夹角的余弦值的绝对值等于异面直线所成角的余弦值求解出结果.
18．
【分析】设圆台的上下底面半径为，利用圆台的体积公式得到，再根据勾股定理得到，联立可得，则可得圆台的侧面积，在侧面展开图中可求出圆心角.
【详解】设圆台的上下底面半径为，
则，化简得，
又因为母线cm，高cm，
所以，即，
所以，即，解得或（舍），
所以，
所以圆台的侧面积为，
圆台的侧面展开图如图：

设小扇形的半径为，圆心角为，
则，所以，
所以，所以，所以，
故答案为：；
19．(1)证明见解析；
(2).

【分析】（1）延长三条侧棱交于点，判断出，为中点.取的中点，证明出和，进而证明出平面，利用面面垂直的判定定理即可证明平面平面.
（2）先由体积关系求出.以为坐标原点，为轴，轴，建立空间直角坐标系，利用向量法求解.
【详解】（1）（1）延长三条侧棱交于点.因为所以， 分别为中点，且.
因为，所以.
取的中点，则.
因为
所以所以.
，则，故，
即.
因为，,平面,平面,
所以平面.
又平面，故平面平面.

（2）因为，所以.
而,
所以，解得：.
以为坐标原点，为轴，轴，建立空间直角坐标系，如图所示，

则，
设为面的一个法向量，
因为，所以，
不妨设，则面的一个法向量.
同理可求得面的一个法向量.
由图示，二面角的平面角为锐角，
所以，
所以二面角的余弦值为.
20．(1)证明见解析
(2)答案见解析

【分析】（1）通过证明平面来证得.
（2）先选择条件，然后根据所选条件，利用几何法或向量法求得二面角的正弦值.
【详解】（1）在三棱柱中，由题意可得，，，
∴，又∵，∴，
同时在中，∵，，∴，
∵平面，
∴平面，
又∵平面，∴.
（2）∵，且，∴平面，
方案一：选择①③
∵平面，∴，，
∴为二面角的平面角，即，
∴，又∵三棱柱的体积为，∴.
法一：取的中点为，连接，，过作于点，连接，
∵平面，∴平面，
又∵，由三垂线定理可得，
∴为二面角的平面角，
其中，，，则，
由于二面角的平面角与二面角的平面角互补，
故二面角的正弦值为.

法二：过作，过作，过作交于点，连接，
∴为二面角的平面角，其中，，，
∴，故二面角的正弦值为.

法三：如图所示，建立空间直角坐标系，
设平面的一个法向量为，且，，
则，令，则，，故，
设平面的一个法向量为，且，，
则，
令，则，，故，
，故二面角的正弦值为.

方案二：选择①②；
解析：过点作于点∵平面平面，，
∴平面，故直线与平面所成角为，且，
设，，则，即，.
余下解法参考方案一.

方案三：选择②③；
∵平面，∴，，
∴为二面角的平面角，即，
过点作于点，
∵平面平面且交线为，，平面，
∴平面，故直线与平面所成角为，且.
设，则，即.
余下解法参考方案一.

21．(1)证明见解析
(2)

【分析】（1）先证明平面∥平面，进而说明∥平面；（2）利用∥平面进行转化，D点到平面的距离等于A点到平面的距离，再证平面，即 ，则．
(1)
取的中点G，连接，则由M，G分别为的中点易得∥
平面，平面
∴∥平面
同理：∥平面
又，
所以平面∥平面，
所以∥平面
(2)
由题意可得∥
平面，平面
∥平面，
所以D点到平面的距离等于A点到平面的距离，
连接,三角形为正三角形，M为中点，所以
平面，平面，所以

∴平面
即，又，设直线与平面所成角为
则．

22．(1)证明见解析
(2)

【分析】（1）取中点Q，连接；先求出，证得，再由证得平面，即可证得；
（2）建立空间直角坐标系，求出，平面的法向量，按照线面角的向量求法求解即可.
(1)
取中点Q，连接；

因为且，所以四边形是菱形，又底面是等腰梯形，
所以，从而，由余弦定理知，
又因为，，
所以，得，
又因，且，
所以平面，所以；
(2)
分别以，为x，y轴，过B作垂直于面的直线为z轴建立空间直角坐标系，

则，，，，
因为，
平面的法向量为，
设直线与平面所成角为，
则，
所以直线与平面所成角的正弦值是.
23．(Ⅰ)证明见解析；(Ⅱ).
【分析】(Ⅰ) 取的中点，连接、，即可证明，，从而得到面面，即可得证；
(Ⅱ) 连接，为二面角的平面角，如图建立空间直角坐标系，利用空间向量法求出线面角的正弦值；
【详解】解：(Ⅰ)取的中点，连接、，因为为的中点，为的中点，所以，，又，所以，因为面，面，面，所以面，面，又，面，所以面面，因为面，所以平面；

(Ⅱ)连接，因为底面是边长2的等边三角形，，所以，，所以为二面角的平面角，即，如图建立空间直角坐标系，则，，，，，所以，，，设面的法向量为，则，令，则，，所以，设直线与平面所成角为，所以
故直线与平面所成角的正弦值为；

24．（1）证明见解析；（2）.
【分析】（1）过P作于E，由面面垂直的性质得面，根据线面垂直的性质有，且△为直角三角形，由线面垂直的判定及性质可证，由线面平行的性质即可证.
（2）构建以E为原点，为x，y，z轴正方向的空间直角坐标系，求的坐标，面PCD的一个法向量，利用空间向量夹角的坐标表示求，即可得直线AP与平面PCD所成角的正弦值.
【详解】（1）由，知：，

过P作于E，又面面，面面，面，
∴面，而面，
∴且，
∵，，易知△为直角三角形且，
∴，而，即面，又面，
∴，又，
∴.
（2）构建以E为原点，为x，y，z轴正方向的空间直角坐标系，如下图示，

∴，，，，则，，，
若面PCD的一个法向量为，则，令即，
∴，即直线AP与平面PCD所成角的正弦值为.
【点睛】关键点点睛：
（1）利用面面垂直的性质证线面垂直，再根据线面垂直的性质及判定证线线垂直，进而由平行四边形的性质即可证结论.
（2）构建空间直角坐标系，利用直线的方向向量与平面法向量夹角的坐标表示求线面角的正弦值.
25．（Ⅰ）证明见解析；（Ⅱ）.
【分析】（Ⅰ）由是矩形得，则，由是等边三角形，得，即可证平面，故得证；
（Ⅱ）法一：用几何法求解，作，依题意可证平面，故即与平面所成角，根据三角知识可求得问题结果；法二：以为原点建立空间直角坐标系，求的方向向量与平面的法向量，结合向量夹角公式即可求解问题．
【详解】（Ⅰ）取中点，连接，在菱形中，且，又因为，所以即二面角的平面角，即
因此是等边三角形，且
显然，且，因此平面
而平面，因此，．

（Ⅱ）法一：因为，即求与平面所成角的正弦值
由（Ⅰ）知平面，而，所以平面
又因为平面，因此，平面平面
作，连接
因为平面平面，且面
所以平面，因此，即与平面所成角
四边形中，，得
中，
与平面所成角的正弦值为
法二：由（Ⅰ）知：平面，而平面，因此平面平面
又因为平面平面，平面，且
因此，平面
如图，以为原点，分别以射线，，为，，轴的正半轴建立空间直角坐标系，则

，，，
因此，，
设平面的法向量，则
，取
记与平面所成角为，则
所以与平面所成角的正弦值为．
【点睛】求直线与平面所成的角的一般步骤：
（1）、①找直线与平面所成的角，即通过找直线在平面上的射影来完成；②计算，要把直线与平面所成的角转化到一个三角形中求解；
（2）、用空间向量坐标公式求解．
26．（Ⅰ）证明见解析；（Ⅱ）.
【分析】（Ⅰ）连结交于，连结，根据棱柱的几何性质，结合线面平行的判定定理进行证明即可.
（Ⅱ）建立空间直角坐标系，利用空间向量夹角公式，结合线面角、面面角定义、同角的三角函数关系式求解即可.
【详解】解：（Ⅰ）连结交于，连结．
∵是三棱柱，∴四边形是平行四边形．
则．
在中，∵，∴．
又平面，平面，∴平面．
（Ⅱ）因为平面，与平面所成角为，即，
又因为在中，，故，，
在中，由余弦定理求得，
过作，，
分别以、、作为轴、轴、轴建立空间直角坐标系．

则，，，
，，，
故，，
设平面的法向量为，则    ．
，取，
又平面的法向量为，
故，所以，
故，
即所求二面角的平面角的正切值为．