2023年小升初『几何问题』专项复习 专题02《等积变形（位移、割补）》 （提高版）

2022-2023学年专题卷

小升初数学几何问题精选真题汇编强化训练（提高）

专题02 等积变形（位移、割补）

考试时间：100分钟；试卷满分：100分

姓名：___________班级：___________考号：___________

一．选择题（共6小题，满分12分，每小题2分）

1．（2分）一个圆柱形橡皮泥，底面积是12.56cm2，高是6cm，如果把它捏成同样底面积大小的圆锥，这个圆锥的高是（　　）cm．

A．2 B．3 C．18 D．36

2．（2分）轧钢厂要把一种底面直径6厘米，长1米的圆柱形钢锭，轧制成内径（内侧直径）为10厘米，外径（外侧直径）为30厘米的无缝钢管，如果不计加工过程中的损耗，则这种无缝钢管的长是（　　）

A．4.25厘米 B．5厘米 C．4厘米 D．4.5厘米

3．（2分）把圆柱的底面平均分成若干等份，切开后，拼成一个长方体，这个长方体与圆柱相比（　　）

A．体积不变，表面积也不变 

B．体积不变，表面积变大 

C．体积变大，面积不变

4．（2分）把割补成后，面积（　　）

A．不变 B．变大了 C．变小了 D．无法判断

5．（2分）如图，长方形的面积与圆的面积相等，已知阴影部分的面积是84.78cm2，圆的周长是（　　）cm．

A．18.84 B．75.36 C．37.68

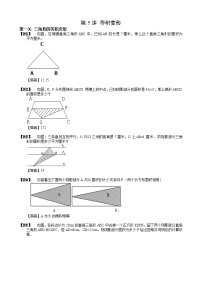
6．（2分）如图的等腰梯形中，甲三角形的面积（　　）乙三角形的面积。

A．大于 B．等于 C．小于 D．无法判断

二．填空题（共8小题，满分16分，每小题2分）

7．（2分）（如图）运用了数学思想方法是 　   　，你还知道哪些数学思想方法？再列举一个 　   　。

8．（2分）把一个底面半径2厘米、高1.5厘米的圆柱形钢锭，铸成底面积大小不变的圆锥形钢锭，圆柱的高和圆锥的高的比是　   　．

9．（2分）如图，大正方形ABCD的边长是10cm，小正方形CGFE的边长是6cm，那么图中阴影部分的面积是 　   　cm2。

10．（2分）将一底面半径为2分米的圆柱的底面平均分成若干个扇形，截开拼成一个和它等底等高的长方体后，表面积增加16平方分米，圆柱的体积是　   　．

11．（2分）有一种饮料瓶的容积是50立方厘米，瓶身呈圆柱形（不包括瓶颈）．现在瓶中装有一些饮料，正放时饮料高度为20厘米，倒放时空余部分的高度为5厘米．瓶内现有饮料　   　立方厘米．

12．（2分）如图，外侧大正方形的边长是10厘米，图中阴影部分的面积是27.5平方厘米，那么圆内的大正方形面积是小正方形面积的　   　倍．

13．（2分）如图，三个大小相同的正方形重叠地放在一个大的正方形ABCD内，已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米．那么正方形ABCD的边长是　   　厘米．

14．（2分）如图所示，一种饮料瓶，容积是200ml，瓶身是圆柱形．将该瓶正放时饮料高20cm，倒放时余部分高5cm，瓶内的饮料是　   　ml．

三．应用题（共14小题，满分72分，每小题5分）

15．（5分）如图所示，SA＝32dm2，SB＝8dm2，h＝5dm．现在要把A处的铁块熔到B处．使A、B处同样高，这时B处比原来升高了多少分米？

16．（5分）如图，一瓶营养液的瓶底直径是12厘米，瓶高30厘米，液面高20厘米，倒置后，液面高25厘米．这个瓶子的容积是多少？

17．（5分）如图1、图2所示，梯形上底AB长3厘米，下底CD长6厘米，高为3厘米，P为CD边上任意一点，求阴影部分的面积。

你认为东东的想法怎么样？写出你这样判断的理由。

18．（5分）如图，正方形ABCD的边长为10厘米，E，F，G，H分别为正方形四边上的

中点，求阴影部分的面积是多少平方厘米．

19．（5分）看图求阴影部分的面积．

（1）求出图（1）中阴影部分的面积．

（2）分析上面各图形之间的关系，看一看、想一想、找一找图（4）中阴影部分的面积是　   　．

20．（5分）如图，正方形ABCD的边长为4cm，则图中阴影部分的面积为多少平方厘米？

21．（5分）给一个直角楼梯铺地毯，如图所示（图中阴影处不铺），至少需要多少平方米的地毯？（单位：米）

22．（5分）雨哗哗地不停地下着．如果在雨地放一个如图1那样的长方体的容器（单位：厘米），雨水将它灌满要用1小时．雨水灌满图2容器各需多长时间？

23．（5分）把一个底面直径是4厘米的圆柱底面分成许多相等的扇形，然后沿着直径切开，拼成一个和它体积相等的长方体，这个长方体的表面积比原来圆柱的表面积增加了20平方厘米，这个长方体的体积是多少立方厘米？

24．（5分）求如图的体积．（π取3.14）

25．（5分）用20个大小相同的小正方可以组成一个十字图形．把这个十字图形分割为4个部分，是的它们的形状和大小都一样（分割线须沿着图内的虚线），方法有很多，如图例所示，请你再画出与范例不同的两种分割方法．

26．（5分）如图，ABCD是一个长方形草坪，长20米，宽14米，中间有一条宽2米的曲折小路，求小路的面积．

27．（6分）A和B都是高度为12厘米的圆柱形容器，底面半径分别是1厘米和2厘米，一水龙头单独向A注水，一分钟可注满．现将两容器在它们的高度的一半出用一根细管连通（连通管的容积忽略不计），仍用该水龙头向A注水，求

（1）2分钟容器A中的水有多高？

（2）3分钟时容器A中的水有多高．

28．（6分） 一个容积为550mL的水瓶，里面装了一些水，正放时，水面高20cm，倒放时，空气高7.5cm．求水有多少升？