2024年高考数学一轮复习（新高考方案）课时跟踪检测（七十三） 成对数据的统计分析

这是一份2024年高考数学一轮复习（新高考方案）课时跟踪检测（七十三） 成对数据的统计分析，共8页。
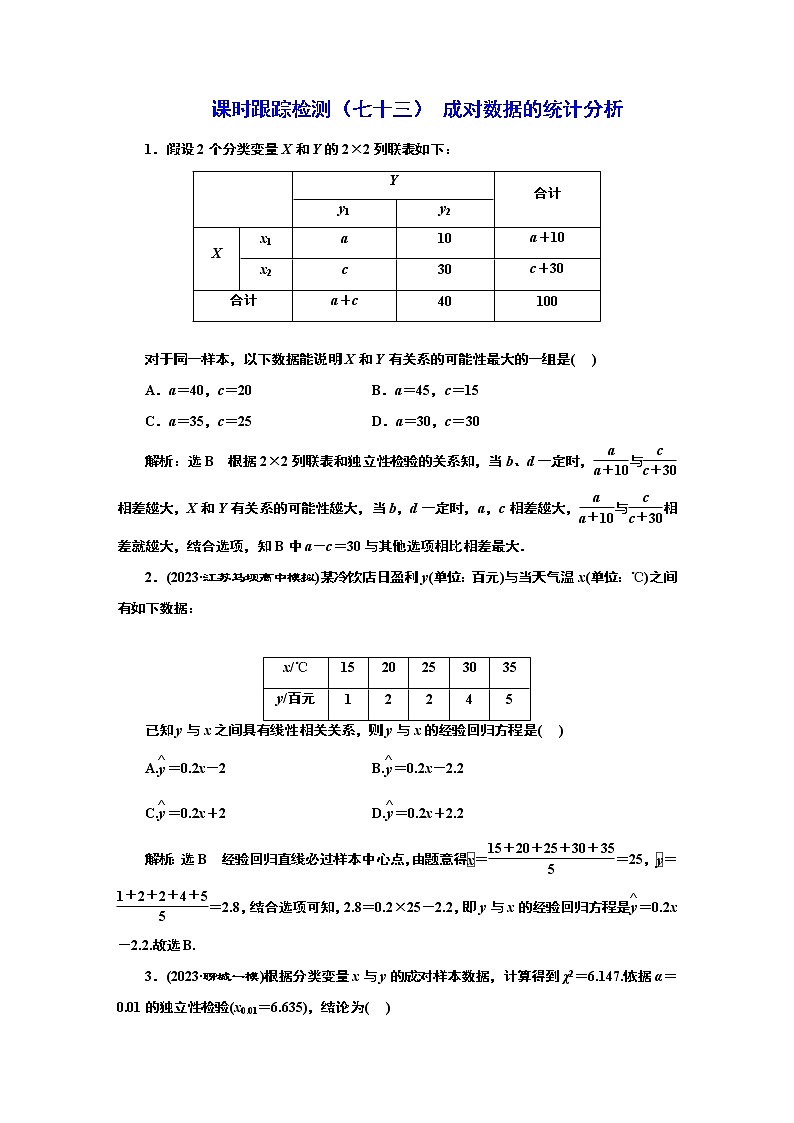
课时跟踪检测（七十三） 成对数据的统计分析1．假设2个分类变量X和Y的2×2列联表如下： Y合计y1y2Xx1a10a＋10x2c30c＋30合计a＋c40100 对于同一样本，以下数据能说明X和Y有关系的可能性最大的一组是(　 )A．a＝40，c＝20  B．a＝45，c＝15C．a＝35，c＝25  D．a＝30，c＝30解析：选B　根据2×2列联表和独立性检验的关系知，当b、d一定时，与相差越大，X和Y有关系的可能性越大，当b，d一定时，a，c相差越大，与相差就越大，结合选项，知B中a－c＝30与其他选项相比相差最大．2．(2023·江苏马坝高中模拟)某冷饮店日盈利y(单位：百元)与当天气温x(单位：℃)之间有如下数据： x/℃1520253035y/百元12245已知y与x之间具有线性相关关系，则y与x的经验回归方程是(　 )A.＝0.2x－2  B.＝0.2x－2.2C.＝0.2x＋2  D.＝0.2x＋2.2解析：选B　经验回归直线必过样本中心点，由题意得＝＝25，＝＝2.8，结合选项可知，2.8＝0.2×25－2.2，即y与x的经验回归方程是＝0.2x－2.2.故选B.3．(2023·聊城一模)根据分类变量x与y的成对样本数据，计算得到χ2＝6.147.依据α＝0.01的独立性检验(x0.01＝6.635)，结论为(　 )A．变量x与y不独立B．变量x与y不独立，这个结论犯错误的概率不超过0.01C．变量x与y独立D．变量x与y独立，这个结论犯错误的概率不超过0.01解析：选C　按照独立性检验的知识及比对的参数值，当χ2＝6.147时，我们可以下结论变量x与y独立，故排除选项A、B；依据α＝0.01的独立性检验(x0.01＝6.635)，6.147<6.635，我们不能得到“变量x与y独立，这个结论犯错误的概率不超过0.01”这个结论， 故C正确，D错误. 故选C.4．色差和色度是衡量毛绒玩具质量优劣的重要指标，现抽检一批产品测得如下数据：色差x212325272931色度y151617212223已知该产品的色差和色度之间满足线性相关关系，且＝0.25x＋，现有一对测量数据为(32,21.25)，则该组数据的残差(测量值与预测值的差)为(　 )A．0.65     B．0.75     C．－0.75      D．0.95解析：选B　样本中心点坐标为(26,19)，代入经验回归方程得到＝12.5，所以＝0.25x＋12.5，将x＝32代入，求解得到对应的预测值为20.5，因而其残差为21.25－20.5＝0.75.故选B.5．(2023·衡阳模拟)某化工厂产生的废气经过过滤后排放，以模型y＝p0e－kx去拟合过滤过程中废气的污染物浓度y mg/L与时间x h之间的一组数据，为了求出经验回归方程，设z＝ln y，其变换后得到经验回归方程为＝－0.5x＋2＋ln 300，则当经过6 h后，预报废气的污染物浓度为(　 )A．300e2  mg/L  B．300e mg/LC. mg/L  D. mg/L解析：选D　当x＝6时，＝－1＋ln 300＝ln ，所以y＝e＝.故选D.6．(2023·莆田模拟)已知变量y关于x的回归方程为y＝ebx－0.5，若对y＝ebx－0.5两边取自然对数，可以发现ln y与x线性相关，现有一组数据如下表所示，x＝5时，预测y值为________.x1234yee3e4e6解析：对y＝ebx－0.5两边取自然对数，得ln y＝bx－0.5，令z＝ln y，则z＝bx－0.5.x1234yee3e4e6z1346＝＝2.5，＝＝3.5，代入＝－0.5得3.5＝·2.5－0.5，故＝1.6，故z＝1.6x－0.5，y＝e1.6x－0.5，当x＝5时，y＝e1.6×5－0.5＝e.答案：e7．(2022·全国甲卷)甲、乙两城之间的长途客车均由A和B两家公司运营．为了解这两家公司长途客车的运行情况，随机调查了甲、乙两城之间的500个班次，得到下面列联表： 准点班次数未准点班次数A24020B21030 (1)根据上表，分别估计这两家公司甲、乙两城之间的长途客车准点的概率；(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关？解：(1)由题表可得A公司甲、乙两城之间的长途客车准点的概率为＝，B公司甲、乙两城之间的长途客车准点的概率为＝.(2)χ2＝≈3.205＞2.706，所以有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关．8．(2023·烟台模拟)为了引导青少年抵制不良游戏，适度参与益脑游戏，某游戏公司开发了一款益脑游戏，在内测时收集了玩家对每一关的平均过关时间，如下表：关卡x123456平均过关时间y(单位：秒)5078124121137352计算得到一些统计量的值为i＝28.5，iui＝106.05，其中，ui＝ln yi.(1)若用模型y＝aebx拟合y与x的关系，根据提供的数据，求出y与x的经验回归方程；(2)制定游戏规则如下：玩家在每关的平均过关时间内通过可获得积分2分并进入下一关，否则获得－1分且该轮游戏结束．甲通过练习，前3关都能在平均时间内过关，后面3关能在平均时间内通过的概率均为，若甲玩一轮此款益脑游戏，求“甲获得的积分X”的分布列和数学期望．参考公式：对于一组数据(xi，yi)(i＝1,2,3，…，n)，其经验回归直线＝x＋的斜率和截距的最小二乘估计分别为＝，＝－.解：(1)因为y＝aebx两边取自然对数可得ln y＝ln(aebx)＝ln a＋ln ebx，即ln y＝ln a＋bx，令u＝ln y，所以u＝bx＋ln a，由＝i＝4.75，＝×(1＋2＋3＋4＋5＋6)＝3.5，＝12＋22＋32＋42＋52＋62＝91.所以＝＝＝0.36，又＝＋ln a，即4.75＝0.36×3.5＋ln a，所以ln a＝3.49，所以a＝e3.49.所以y关于x的经验回归方程为y＝e0.36x＋3.49.(2)由题知，甲获得的积分X的所有可能取值为5,7,9,12，所以P(X＝5)＝，P(X＝7)＝×＝，P(X＝9)＝2×＝，P(X＝12)＝3＝，所以X的分布列为X57912P所以E(X)＝5×＋7×＋9×＋12×＝.9．小李准备在某商场租一间商铺开服装店，为了解市场行情，在该商场调查了20家服装店，统计得到了它们的面积x(单位：m2)和日均客流量y(单位：百人)的数据(xi，yi)(i＝1,2，…，20)，并计算得i＝2 400，i＝210，(xi－)2＝42 000，(xi－)(yi－)＝6 300.(1)求y关于x的经验回归方程；(2)已知服装店每天的经济效益W＝k＋mx(k>0，m>0)，该商场现有60～150  m2的商铺出租，根据(1)的结果进行预测，要使单位面积的经济效益Z最高，小李应该租多大面积的商铺？附：经验回归直线＝x＋的斜率和截距的最小二乘估计分别为＝，＝－. 解：(1)由已知可得＝i＝120，＝i＝10.5，＝＝＝0.15，＝－＝10.5－0.15×120＝－7.5，所以经验回归方程为＝0.15x－7.5.(2)根据题意得Z＝＝＋m，60≤x≤150.设f(x)＝＝－，令t＝，≤t≤，则f(x)＝g(t)＝0.15t－7.5t2＝－7.5(t－0.01)2＋0.000 75，当t＝0.01，即x＝100时，f(x)取最大值，又因为k，m>0，所以此时Z也取最大值，因此，小李应该租100 m2的商铺．10．某公司对项目A进行生产投资，所获得的利润有如下统计数据表：  项目A投资金额x(单位：百万元)12345所获利润y(单位：百万元)0.30.30.50.91(1)请用线性回归模型拟合y与x的关系，并用样本相关系数加以说明；(2)该公司计划用7百万元对A，B两个项目进行投资，若公司对项目B投资x(1≤x≤6)百万元所获得的利润y近似满足：y＝0.16x－＋0.49，求A，B两个项目投资金额分别为多少时，获得的总利润最大？附：①对于一组数据(x1，y1)，(x2，y2)，…，(xn，yn)，其经验回归方程＝x＋的斜率和截距的最小二乘法估计公式分别为＝，＝－.②样本相关系数r＝.一般地，样本相关系数r的绝对值在0.75以上(含0.75)认为线性相关程度较强；否则，线性相关程度较弱．参考数据：对项目A投资的统计数据表中iyi＝11，＝2.24，≈2.1.解：(1)对项目A投资的统计数据进行计算得，＝3，＝0.6，＝55，于是得＝＝＝0.2，＝－＝0.6－0.2×3＝0.所以经验回归方程为＝0.2x.样本相关系数r＝＝＝≈0.952 4>0.75，这说明投资金额x与所获利润y之间的线性相关程度较强，用经验回归方程＝0.2x对该组数据进行拟合合理．(2)设对B项目投资x(1≤x≤6)百万元，则对A项目投资(7－x)百万元，所获总利润W＝0.16x－＋0.49＋0.2(7－x)＝1.93－≤1.93－2＝1.65，当且仅当0.04(x＋1)＝，即x＝2.5时取等号，所以对A，B项目分别投资4.5百万元，2.5百万元时，获得总利润最大．11．已知一系列样本点(x1，y1)，(x2，y2)，…，(xn，yn)，其中n∈N*，n≥2.响应变量y关于x的线性回归方程为＝＋x，对于响应变量y，通过观测得到的数据称为观测值，通过线性回归方程得到的称为预测值，观测值减去预测值，称为残差，即i＝yi－i＝yi－xi－(i＝1,2，…，n)，称为相应于点(xi，yi)的残差．证明：(1)i＝0；(2)＝(1－r2)(yi－)2，并说明|r|与线性回归模型拟合效果的关系．参考公式：r＝，＝，＝－.证明：(1)∵i＝yi－i，∴i＝i－i，且i＝＋xi，＝－，∴i＝(＋xi)，＝＋，∴i＝n－(＋xi)＝n(＋)－n－n＝0.(2)根据给出的样本相关系数公式，以及经验回归直线斜率和截距的最小二乘估计公式，可知(xi－)(yi－)＝(xi－)2，记R2＝1－＝1－，∴2(xi－)(yi－)－2(xi－)2＝2(xi－)2，且2(xi－)(yi－)－2(xi－)2＝(xi－) [2(yi－)－(xi－)]＝(2yi－－i)·(i－)＝(yi－)2－(yi－i)2＝R2(yi－)2，又2(xi－)2＝＝r2(yi－)2＝R2(yi－)2，∴r2＝R2，又R2＝r2＝1－，∴＝(1－r2)(yi－)2，且当越小时，相关性越强，线性回归模型拟合效果越好，即|r|越接近于1时，线性回归模型拟合效果越好．