2022-2023学年河北省石家庄市高一上学期期末数学试题含解析

2022-2023学年河北省石家庄市高一上学期期末数学试题

一、单选题

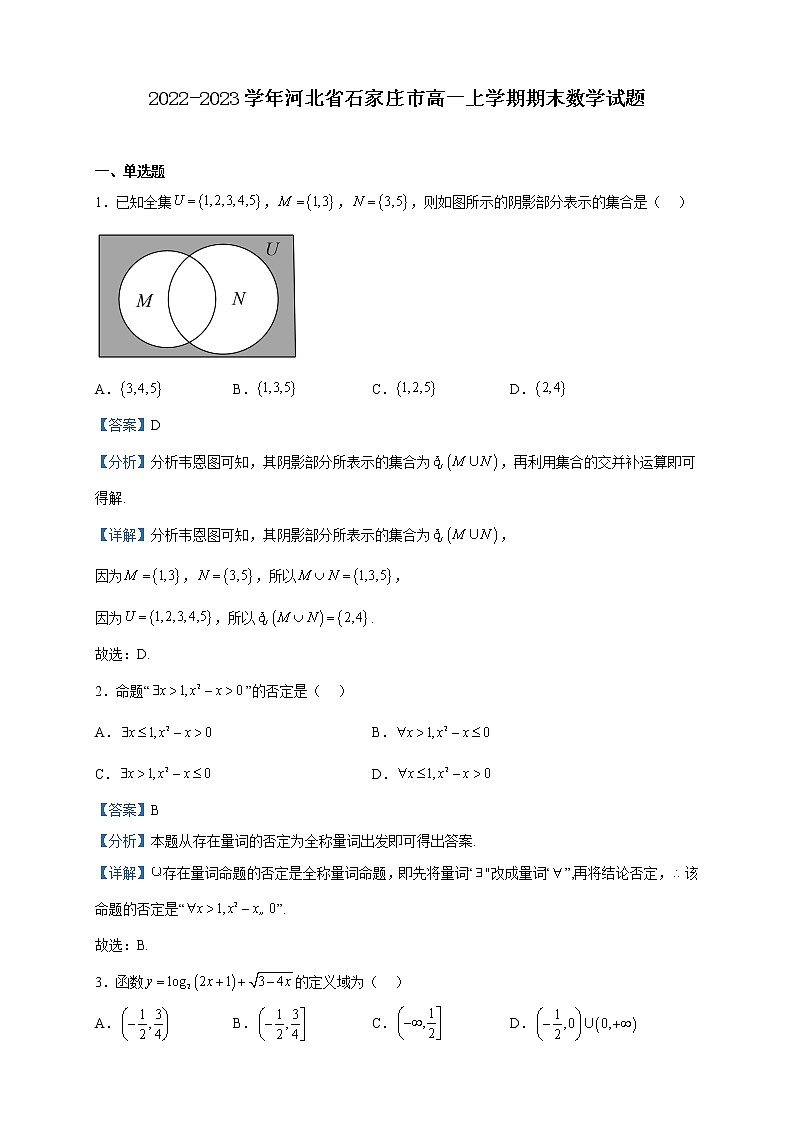
1．已知全集，，，则如图所示的阴影部分表示的集合是（    ）

A． B． C． D．

【答案】D

【分析】分析韦恩图可知，其阴影部分所表示的集合为，再利用集合的交并补运算即可得解.

【详解】分析韦恩图可知，其阴影部分所表示的集合为，

因为，，所以，

因为，所以.

故选：D.

2．命题“”的否定是（    ）

A． B．

C． D．

【答案】B

【分析】本题从存在量词的否定为全称量词出发即可得出答案.

【详解】存在量词命题的否定是全称量词命题，即先将量词“"改成量词“”,再将结论否定，该命题的否定是“”.

故选：B.

3．函数的定义域为（    ）

A． B． C． D．

【答案】B

【分析】令，解不等式可得答案．

【详解】令，解得，故定义域为.

故选：B.

4．已知角的终边经过点，则的值为（    ）

A． B． C． D．

【答案】A

【分析】利用三角函数的定义即可得解.

【详解】因为角的终边经过点，

所以.

故选：A.

5．设，，，则（    ）

A． B． C． D．

【答案】D

【分析】利用对数函数、指数函数的单调性确定的范围，进而比较大小可得答案.

【详解】因为在上单调递增，

所以，即；

因为在上单调递增，

所以，

因为在上单调递减，

所以，

所以.

故选：D．

6．函数的图象大致是（    ）

A． B．

C． D．

【答案】C

【分析】先判断函数奇偶性，排除A、D选项，再根据排除B选项，即可得结果.

【详解】函数定义域为,且，

所以为偶函数，排除A、D选项；

因为，所以排除B，

故选：C.

7．数学中常用记号表示p，q两者中较大的一个，用表示p，q两者中较小的一个，若函数的图象关于对称，则t的值为（    ）

A． B．2 C． D．1

【答案】D

【分析】先分析与的图像性质，再在同一个坐标系中作出两个函数的图像，结合图像可分析得的图像关于直线对称，从而求得值．

【详解】对于，易得其图像关于轴对称；

对于，易得其图像关于对称；

如图，在同一个坐标系中做出两个函数与的图象，

则函数的图象为两个图象中较低的一个，

结合图像可知的图象关于直线对称，

所以要使函数的图象关于直线对称，

则，故．

故选：D.

8．已知函数在上单调递增，则a的取值范围是（    ）

A． B．

C． D．

【答案】B

【分析】先利用指数函数与一次函数的单调性，分段讨论的单调性，从而得到，再由在上的单调性得处有，从而得到，由此得解.

【详解】因为在上单调递增，

当时，在上单调递增，所以；

当时，在上单调递增，所以，即；

同时，在处，，即，即，

因为，所以，即，

解得或（舍去），

综上：，即.

故选：B.

二、多选题

9．已知函数图象经过点，则下列命题正确的有（    ）

A．函数为奇函数

B．函数在定义域内为减函数

C．若，则

D．若，则

【答案】AC

【分析】将点代入函数得到，利用函数奇偶性的定义可判断A，举反例可判断BD，利用作差法可判断D.

【详解】因为图象经过点，

所以，即，则，

对于A，易得的定义域为，关于原点对称，

又，所以为奇函数，故A正确；

对于B，，函数不是减函数，故B错误；

对于C，因为，

所以，即，故C正确.

对于D，，故D错误；

故选：AC.

10．成立的充分不必要条件可以是（    ）

A． B．

C． D．

【答案】BC

【分析】先求得的等价条件，再利用充分不必要条件的性质得到集合的包含关系，从而得解.

【详解】令，，

由得，故，

若是成立的充分不必要条件，则是的真子集，

对于A，不是的真子集，故A错误；

对于B，是的真子集，故B正确；

对于C，是的真子集，故C正确；

对于D，不是的真子集，故D错误；

故选：BC.

11．下列函数中以为周期的是（    ）

A． B．

C． D．

【答案】AD

【分析】对于ABD，利用三角函数的性质以及周期公式逐一判断即可；对于C，举例子证明不是周期函数即可判断.

【详解】对于A，，则，故A正确；

对于B，，则，

所以不以为周期，故B错误；

对于C，因为，

所以，，

所以至少存在，使得，

所以不是以为周期的周期函数，故C错误；

对于D，，则，故D正确.

故选：AD.

12．已知正数x、y，满足，则下列说法正确的是（    ）

A．xy的最大值为1 B．的最大值为2

C．的最小值为 D．的最小值为1

【答案】ABD

【分析】对于AB，利用基本不等式及其推论即可判断；对于CD，利用换元法与基本不等式“1”的妙用即可判断.

【详解】对于A，因为，

所以，则，

当且仅当且，即时，等号成立，

所以xy的最大值为1，故A正确；

对于B，因为，

所以，当且仅当时，等号成立，

所以，则，

当且仅当且，即时，等号成立，

所以的最大值为2，故B正确；

对于C，，

当且仅当且，即时等号成立，

所以的最小值为，故C错误；

对于D，令，，则，，，，

所以

，

当且仅当且，即，即时，等号成立，

所以的最小值为1，故D正确.

故选：ABD.

【点睛】方法点睛：在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．

三、填空题

13．已知，，则__________.

【答案】

【分析】利用诱导公式转化为锐角的三角函数求解.

【详解】∵，∴，

∵，

∴，.

故答案为：.

14．斐波那契螺旋线被称为自然界最完美的“黄金螺旋”，它的画法是：以斐波那契数1，1，2，3，5，8……为边长的正方形按如图的方式拼成长方形，并以每个正方形的某一顶点为圆心画一个圆心角为的圆弧，这些圆弧连成的弧线被称为斐波那契螺旋线，图中的弧线就是斐波那契螺旋线的前一部分，则阴影部分的面积与矩形ABCD的面积之比为________．

【答案】/

【分析】由圆的面积公式和矩形的面积公式，分别求得其面积，即可得解.

【详解】由题意知，矩形的面积为，

而阴影部分的面积为，

所以阴影部分的面积与矩形的面积之比为.

故答案为：.

15．已知函数在区间上有零点，则实数m的取值范围是________．

【答案】

【分析】先利用基本初等函数的单调性判断得在上都单调递增，再利用零点存在定理得到，解之即可得解.

【详解】因为与在上都单调递增，

所以在上单调递增，

因为在区间上有零点，

所以，即，即，

解得，

所以实数m的取值范围为.

故答案为：.

四、双空题

16．已知是偶函数，则________，的最小值为________．

【答案】         

【分析】先利用函数奇偶性的定义可求得实数的值，从而得到，再利用基本不等式即可推得，由此得解.

【详解】因为函数为偶函数，则，

即，

所以，

由的任意性可得，故，

所以，

因为，所以，

当且仅当，即时，等号成立，即，

所以，即的最小值为.

故答案为：；.

五、解答题

17．已知，且，求的值．

【答案】

【分析】利用诱导公式和同角三角函数关系得，再结合同角三角函数的商的关系求出的值，代入计算即可.

【详解】设,,那么,从而.

于是.因为,

所以.由,得.

所以,

所以.

，

则.

18．已知全集为，集合，．

(1)若，求集合；

(2)请在①“”是“”的充分条件，②，③这三个条件中任选一个，补充在下面问题的横线上，并完成问题解答．

若________，求实数a的取值范围．

【答案】(1)或

(2)或.

【分析】（1）直接根据集合的补集以及交集的定义计算即可；

（2）若选①，则可知，列出相应的不等式，解得答案；若选②，求出，再根据集合的交集运算，列出相应的不等式，解得答案；若选③，根据集合的并集运算，列出相应的不等式，解得答案；

【详解】（1）集合或，集合，

若，

所以或

所以或.

（2）若选①“”是“”的充分条件，则，

即或，

所以或，

或；

若选②，

所以或

或

若选③，，

则或，或.

19．设（，且）其图象经过点，又的图象与的图象关于直线对称．

(1)若在区间上的值域为，且，求c的值；

(2)若，，求的值．

【答案】(1)

(2)

【分析】（1）将点代入解析式，即可求出，根据其单调性得，则，解出即可；

（2）根据指数函数与对数函数的关系得，则有，则.

【详解】（1）因为（，且）的图象经过点，

所以，所以，所以，所以，

因为在区间上单调递增，则，

因为，所以，所以，

即，解得.

（2）的图象与的图象关于直线对称，

，若，则，，

所以，所以.

20．已知函数的图象相邻两条对称轴之间的距离为．

(1)求的解析式和单调递增区间；

(2)求函数在区间上值域．

【答案】(1)，单调增区间为.

(2)

【分析】（1）根据正弦型函数的性质得出的值，结合正弦函数的单调性确定函数的单调递增区间；

（2）根据正弦函数的性质得出，进而得出函数在区间上的值域.

【详解】（1）因为相邻两条对称轴之间的距离为，所以的最小正周期，

所以，，则， ，

又因为当，时函数单调递增，

即，,

所以函数的单调递增区间为；

（2）（2）当时，，所以

所以函数在区间的值域为.

21．酒驾是严重危害交通安全的违法行为，为了保障交通安全，根据国家有关规定：血液中酒精含量达到的驾驶员即为酒后驾车，及以上认定为醉酒驾车．假设人在喝一定量的酒后，如果停止喝酒，血液中的酒精含量会以每小时p的比率减少．现有驾驶员甲乙三人喝了一定量的酒后，测试他们血液中的酒精含量均上升到了．（运算过程保留4位小数，参考数据：，．．，）

(1)若驾驶员甲停止喝酒后，血液中酒精含量每小时下降比率为，则驾驶员甲至少要经过多少个小时才能合法驾驶？（最后结果取整数）

(2)驾驶员乙在停止喝酒5小时后驾车，却被认定为酒后驾车，请你结合（1）的计算，从数学角度给驾驶员乙简单分析其中的原因，并为乙能够合法驾驶提出合理建议；

(3)驾驶员乙听了你的分析后，在不改变饮酒量的条件下，在停止饮酒后6小时和7小时各测试一次并记录结果，经过一段时间观察，乙发现自己至少要经过7个小时才能合法驾驶．请你帮乙估算一下：他停止饮酒后，血液中酒精含量每小时减少比率的取值范围．（最后结果保留两位小数）

【答案】(1)驾驶员甲至少要经过个小时才能合法驾驶

(2)答案见解析

(3)

【分析】（1）根据题意得到，利用对数运算法则与换底公式运算即可得解；

（2）根据（1）中计算结果，给予驾驶员乙合理的建议即可；

（3）设驾驶员乙停止喝酒后，血液中酒精含量每小时下降比率为，根据题意得到关于的不等式组，解之即可.

【详解】（1）根据题意，驾驶员甲停止喝酒后，经过t小时后，体内的酒精含量为，

只需，即，所以，

可得，

取整数为时，满足题意.

所以驾驶员甲至少要经过个小时才能合法驾驶.

（2）因为驾驶员乙在停止喝酒5小时后驾车，却被认定为酒后驾车，

说明驾驶员乙血液中的酒精含量每小时下降比率比驾驶员甲小，

所以驾驶员乙在停止喝酒5小时后其血液中的酒精含量大于国家有关规定的含量，

故此，建议驾驶员乙在停止饮酒后的若干个小时进行测试其血液中的酒精含量，从而确定自己停止饮酒后需要经过多少小时，才能合法驾驶.

（3）设驾驶员乙停止喝酒后，血液中酒精含量每小时下降比率为，

则经过小时后，驾驶员乙体内的酒精含量为，

根据题意可知，驾驶员乙在停止喝酒6小时后其血液中的酒精含量仍不达标，在7小时后其血液中的酒精含量达标，

所以，

对于，即，则，故；

对于，即，则，故；

综上：，

所以驾驶员乙停止饮酒后，血液中酒精含量每小时减少比率的取值范围为.

22．已知函数（a，b，）有最小值，且的解集为．

(1)求函数的解析式；

(2)若对于任意的，不等式恒成立，求实数m的取值范围．

【答案】(1)

(2)

【分析】（1）根据韦达定理列出方程组解出即可；

（2）分离参数得，，利用基本不等式求出右边最值即可.

【详解】（1）令，则为方程的两根，则，

则由题有，解得，

.

（2）由（1）得对，，

即，，，

，

令，，则，

当且仅当，即时等号成立，

故，则.