2023年湖北省黄冈市浠水县方铺中学中考数学二模试卷(含答案解析)

这是一份2023年湖北省黄冈市浠水县方铺中学中考数学二模试卷(含答案解析)，共26页。试卷主要包含了008×107C， 因式分解等内容，欢迎下载使用。
2023年湖北省黄冈市浠水县方铺中学中考数学二模试卷
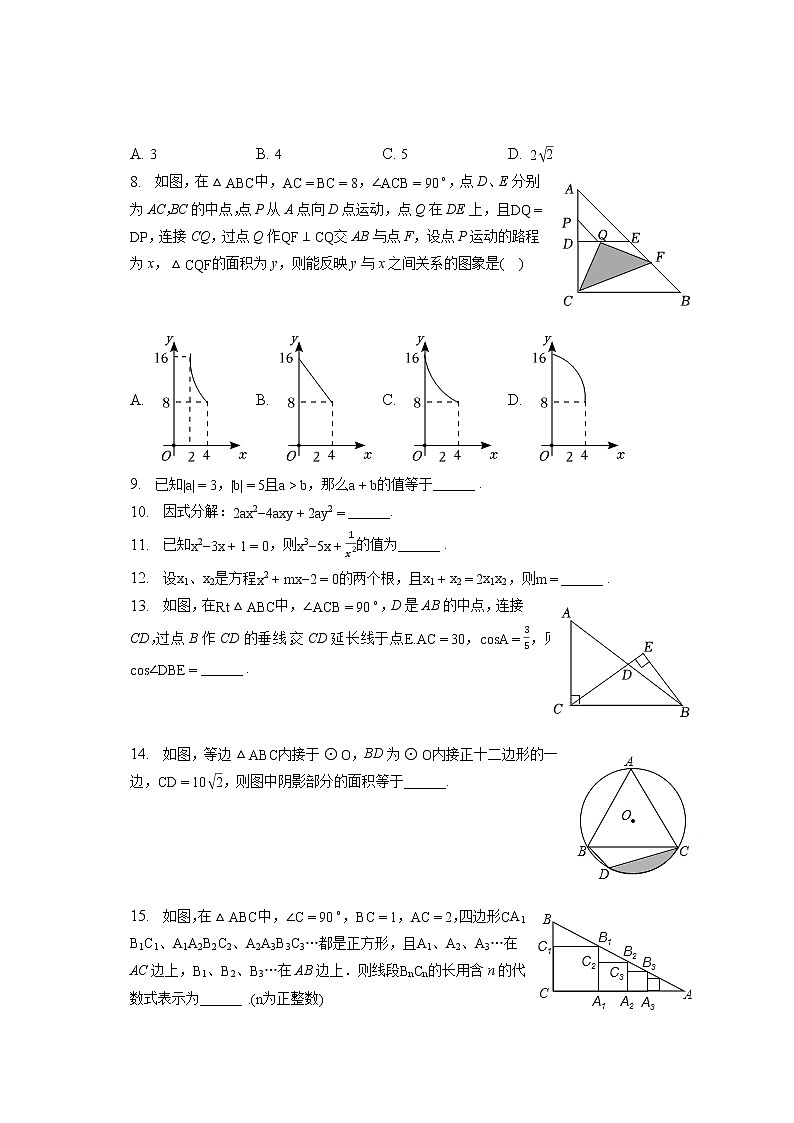
1. 下列各组数中，互为相反数的一组是(    )
A. 131和1−31 B. 7和− 7 C. 13和 19 D. 52和(−5)2
2. 数据50080000用科学记数法表示为(    )
A. 5008×104 B. 5.008×107 C. 5.08×107 D. 5.8×108
3. 如图的几何体，从左面看的平面图是(    )
A.
B.
C.
D.
4. 如图，数轴上点A表示的实数是(    )

A. 5−1 B. 5+1 C. 3+1 D. 3−1
5. 如图，△ABC内接于⊙O，并且AB为⊙O的直径，∠B=35∘，点P是BC上任意一点(点P不与点C，点B重合)，连接PA，则∠PAB的度数不可能为(    )


A. 40∘ B. 45∘ C. 50∘ D. 60∘
6. 方程2x2−5x+3=0的根的情况是(    )
A. 有两个相等的实数根 B. 没有实数根
C. 有两个不相等的实数根 D. 只有一个实数根
7. 如图，矩形ABCD中，AB=4，BC=8，E为CD边的中点，点P、Q为BC边上的两个动点，且PQ=2，当BP=时，四边形APQE的周长最小.(    )


A. 3 B. 4 C. 5 D. 2 2
8. 如图，在△ABC中，AC=BC=8，∠ACB=90∘，点D、E分别为AC，BC的中点，点P从A点向D点运动，点Q在DE上，且DQ=DP，连接CQ，过点Q作QF⊥CQ交AB与点F，设点P运动的路程为x，△CQF的面积为y，则能反映y与x之间关系的图象是(    )


A. B. C. D.
9. 已知|a|=3，|b|=5且a>b，那么a+b的值等于______ .
10. 因式分解：2ax2−4axy+2ay2=______.
11. 已知x2−3x+1=0，则x3−5x+1x2的值为______ .
12. 设x1、x2是方程x2+mx−2=0的两个根，且x1+x2=2x1x2，则m=______ .
13. 如图，在Rt△ABC中，∠ACB=90∘，D是AB的中点，连接CD，过点B作CD的垂线，交CD延长线于点E.AC=30，cosA=35，则cos∠DBE=______ .


14. 如图，等边△ABC内接于⊙O，BD为⊙O内接正十二边形的一边，CD=10 2，则图中阴影部分的面积等于______.


15. 如图，在△ABC中，∠C=90∘，BC=1，AC=2，四边形CA1B1C1、A1A2B2C2、A2A3B3C3…都是正方形，且A1、A2、A3…在AC边上，B1、B2、B3…在AB边上．则线段BnCn的长用含n的代数式表示为______ .(n为正整数)
16. 如图，在Rt△ABC中，∠C=90∘，BC=2 3，AC=2，点D是BC的中点，点E是边AB上一动点，沿DE所在直线把△BDE翻折到△B′DE的位置，B′D交AB于点F.若△AB′F为直角三角形，则AE的长为______.


17. 计算：3−27+12 16+|− 2|+1.
18. 如图1，平行四边形ABCD中，点E、F在直线BD上，且BE=DF，连接AF，FC，CE，EA.
(1)求证：四边形AFCE是平行四边形；
(2)如图2，连接AC，若AC⊥BD，请直接写出图中与AF相等的三条线段(不包括AF).

19. “1000米跑步”是体育中考的必考项目，某校为了了解学生长跑能力，学校从初三800名学生中随机抽取部分学生进行测试，并将跑步时间折算成得分绘制统计图(部分信息未给出)，其中扇形统计图中8分的圆心角度数为90∘.

由图中给出的信息解答下列问题：
(1)求抽取学生的总人数，并补全频数分布直方图；
(2)如果全体初三学生都参加测试，请你根据抽样测试的结果估计该校初三学生获得10分学生的人数；
(3)经过一段时间训练，学校将从之前抽测获得7分的3位同学(2名男生，1名女生)当中抽取2人再次测试，请用列表或者画树状图的方法计算恰好抽到的都是男生概率.
20. 如图，双曲线C1：y=k1x与直线y=2x+b在第一象限交于点A(1,6).
(1)求双曲线与直线的解析式；
(2)曲线C2是反比例函数y=k2x在第四象限的分支，点B是C2上的一点，且△ABO是等腰直角三角形，∠AOB=90∘，求C2的解析式；
(3)是否在x轴上存在一点P，使|PA−PB|的值最大，若存在，直接写出点P的坐标；若不存在，说明理由.

21. 如图，⊙O是四边形ABCD的外接圆．AC、BD是四边形ABCD的对角线，BD经过圆心O，点E在BD的延长线上，BA与CD的延长线交于点F，DF平分∠ADE.
(1)求证：AC=BC；
(2)若AB=AF，求∠F的度数；
(3)若CDAC=12，⊙O半径为5，求DF的长．

22. 四边形ABCD是正方形，E是直线BC上一点，连接AE，在AE右侧，过点E作射线EP⊥AE，F为EP上一点.
(1)如图1，若点E是BC边的中点，且EF=AE，连接CF，则∠DCF=______ ∘；
(2)如图2，若点E是BC边上一点(不与B，C重合).∠DCF=45∘，判断线段EF与AE的数量关系，并说明理由；
(3)若正方形边长为1，且EF=AE，当AF+BF取最小值时，求△BCF的面积.

23. 有一种葡萄：从树上摘下后不保鲜最多只能存放一周，如果放在冷藏室，可以延长保鲜时间，但每天仍有一定数量的葡萄变质，假设保鲜期内的重量基本保持不变，现有一位个体户，按市场价收购了这种葡萄200千克放在冷藏室内，此时市场价为每千克2元，据测算，此后每千克鲜葡萄的市场价格每天可以上涨0.2元，但是，存放一天需各种费用20元，平均每天还有1千克葡萄变质丢弃．
(1)设5天后每千克鲜葡萄的市场价为P元，则P=______ ；
(2)若存放x天后将鲜葡萄一次性出售，销售金额为760元，求x的值？
(3)问个体户将这批葡萄存放多少天后出售，可获得最大利润？最大利润Q是多少？
24. 如图1，抛物线y=ax2+3x−6与x轴交于A、B(6,0)两点，与y轴交于点C，直线y=x+b经过点B.点P在抛物线上，设点P的横坐标为m.

(1)①求抛物线的表达式和b的值；②连接AC、AP、PC，若△APC是以CP为斜边的直角三角形，求点P的坐标；
(2)如图2，若点P在直线BC上方的抛物线上，过点P作PQ⊥BC，垂足为Q，求CQ+PQ的最大值.
答案和解析

1.【答案】B 
【解析】解：∵1−31=−30，
∴131和1−31不是互为相反数，
∴A选项不符合题意；
∵ 7和− 7互为相反数，
∴B选项符合题意；
∵ 19=13，
∴13和 19不是互为相反数，
∴C选项不符合题意；
∵52=25，(−5)2=25，
∴52与(−5)2不是互为相反数，
∴D选项不符合题意，
故选：B.
利用相反数的意义对每个选项进行逐一判断即可得出结论．
本题主要考查了相反数的意义，实数的性质，熟练掌握相反数的有意义是解题的关键．

2.【答案】B 
【解析】解：50080000=5.008×107.
故选：B.
科学记数法的表示形式为a×10n的形式，其中1≤|a|b，
∴a=3，b=−5和a=−3，b=−5.
∴a+b=−2或a+b=−8.
故答案为：−2或−8.
求出a，b的值，根据a>b，确定a，b的值，进而求出解．
本题考查有理数的加法和绝对值的概念，以及对a>b条件的理解．

10.【答案】2a(x−y)2 
【解析】
【分析】
本题考查了提公因式法与公式法的综合运用，属于基础题．
原式提取公因式2a，再利用完全平方公式分解即可．
【解答】
解：原式=2a(x2−2xy+y2)=2a(x−y)2，
故答案为：2a(x−y)2.  
11.【答案】5 
【解析】解：∵x2−3x+1=0，
∴x2−3x+1x=x−3+1x=0，x2=3x−1，x2−3x=−1，
∴x+1x=3，
∴(x+1x)2=2+x2+1x2=9，
∴x2+1x2=9−2=7，
∴x3−5x+1x2
=x(x2−5)+1x2
=x(3x−6)+1x2=3x2−6x+1x2
=2x2−6x+x2+1x2
=2(x2−3x)+x2+1x2
=−2+x2+1x2
=−2+7=5.
故答案为：5.
将方程x2−3x+1=0同除以x，得到x+1x=3，进而求出x2+1x2=7，将x3−5x+1x2进行化简，利用整体思想代入求值即可．
本题考查分式的化简求值，熟练掌握完全平方公式，利用整体思想进行求值是解题的关键．

12.【答案】4 
【解析】解：∵x1、x2是方程x2+mx−2=0的两个根，
∴x1+x2=−m，x1x2=−2.
∵x1+x2=2x1x2，
∴−m=2×(−2)，
解得m=4.
故答案为：4.
由根与系数的关系可得x1+x2=−m，x1x2=−2，结合x1+x2=2x1x2可得出关于m的一元一次方程，解之即可得出结论．
本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0(a≠0)的两根时，x1+x2=−ba，x1⋅x2=ca.

13.【答案】2425 
【解析】解：过点C作CF⊥AB，垂足为F，

在Rt△ABC中，AC=30，cosA=35，
∴AB=ACcosA=3035=50，
∴BC= AB2−AC2= 502−302=40，
∵D是AB的中点，
∴CD=12AB=25，
∵△ABC的面积=12AB⋅CF=12AC⋅CB，
∴AB⋅CF=AC⋅CB，
∴50CF=30×40，
∴CF=24，
在Rt△CDF中，DF= CD2−CF2= 252−242=7，
∴cos∠DCF=CFCD=2425，
∵BE⊥CD，
∴∠E=90∘，
∴∠EDB+∠EBD=90∘，
∵∠FCD+∠CDF=90∘，∠CDF=∠BDE，
∴∠EBD=∠DCF，
∴cos∠DBE=cos∠DCF=2425，
故答案为：2425.
过点C作CF⊥AB，垂足为F，在Rt△ABC中，利用锐角三角函数的定义求出AB=50，从而利用勾股定理求出BC=40，然后利用直角三角形斜边上的中线性质可得CD=12AB=25，再利用面积法求出CF=24，从而在Rt△CDF中，利用勾股定理求出DF=7，进而利用锐角三角函数的定义求出cos∠DCF的值，最后利用等角的余角相等可得∠EBD=∠DCF，即可解答．
本题考查了解直角三角形，掌握直角三角形斜边上的中线等于斜边的一半，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．

14.【答案】25π−50 
【解析】解：连接OB，OC，OD，

∵等边△ABC内接于⊙O，BD为内接正十二边形的一边，
∴∠BOC=13×360∘=120∘，∠BOD=112×360∘=30∘，
∴∠COD=∠BOC−∠BOD=90∘，
∵OC=OD，
∴∠OCD=45∘，
∴OC=CD⋅cos45∘=10 2× 22=10(cm).
∴阴影部分的面积=90π×102360−12×10×10=25π−50.
故答案为：25π−50.
首先连接OB，OC，OD，由等边△ABC内接于⊙O，BD为内接正十二边形的一边，可求得∠BOC，∠BOD的度数，继而证得△COD是等腰直角三角形，继而求得答案．
此题考查了正多边形与圆以及等腰直角三角形性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．

15.【答案】(23)n 
【解析】
【分析】
根据题意得出△BB1C1∽△BAC，进而求出B1C1=23，同理可得出：B2C2=(23)2，B3C3=(23)3…进而得出答案．
此题主要考查了相似三角形的判定与性质，得出线段BnCn长的变化规律是解题关键．
【解答】
解：由题意可得：B1C1//AC，
∴△BB1C1∽△BAC，
∴BC1BC=B1C1AC，
∵CC1=B1C1，
∴B1C12=1−C1B11，
解得：B1C1=23，
故A1B1=23，AA1=43，
同理可得出：B2C2=(23)2，B3C3=(23)3…
∴线段BnCn的长用含n的代数式表示为：(23)n.
故答案为：(23)n.  
16.【答案】3或145 
【解析】解：∵∠C=90∘，BC=2 3，AC=2，
∴tanB=ACBC=22 3= 33，
∴∠B=30∘，
∴AB=2AC=4，
∵点D是BC的中点，沿DE所在直线把△BDE翻折到△B′DE的位置，B′D交AB于点F
∴DB=DC= 3，EB′=EB，∠DB′E=∠B=30∘，
设AE=x，则BE=4−x，EB′=4−x，
当∠AFB′=90∘时，
在Rt△BDF中，cosB=BFBD，
∴BF= 3cos30∘=32，
∴EF=32−(4−x)=x−52，
在Rt△B′EF中，∵∠EB′F=30∘，
∴EB′=2EF，
即4−x=2(x−52)，解得x=3，此时AE为3；
若B′不落在C点处，作EH⊥AB′于H，连接AD，如图，
∵DC=DB′，AD=AD，
∴Rt△ADB′≌Rt△ADC，
∴AB′=AC=2，
∵∠AB′E=∠AB′F+∠EB′F=90∘+30∘=120∘，
∴∠EB′H=60∘，
在Rt△EHB′中，B′H=12B′E=12(4−x)，EH= 3B′H= 32(4−x)，
在Rt△AEH中，∵EH2+AH2=AE2，
∴34(4−x)2+[12(4−x)+2]2=x2，解得x=145，此时AE为145.
综上所述，AE的长为3或145.
故答案为3或145.
利用三角函数的定义得到∠B=30∘，AB=4，再利用折叠的性质得DB=DC= 3，EB′=EB，∠DB′E=∠B=30∘，设AE=x，则BE=4−x，EB′=4−x，讨论：当∠AFB′=90∘时，则∴BF= 3cos30∘=32，则EF=32−(4−x)=x−52，于是在Rt△B′EF中利用EB′=2EF得到4−x=2(x−52)，解方程求出x得到此时AE的长；若B′不落在C点处，作EH⊥AB′于H，连接AD，如图，证明Rt△ADB′≌Rt△ADC得到AB′=AC=2，再计算出∠EB′H=60∘，则B′H=12(4−x)，EH= 32(4−x)，接着利用勾股定理得到34(4−x)2+[12(4−x)+2]2=x2，方程求出x得到此时AE的长．
本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了含30度的直角三角形三边的关系和勾股定理．

17.【答案】解：3−27+12 16+|− 2|+1
=−3+12×4+ 2+1
=−3+2+ 2+1
= 2. 
【解析】首先计算开方、开立方和绝对值，然后计算乘法，最后从左向右依次计算，求出算式的值即可．
此题主要考查了实数的运算，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．

18.【答案】(1)证明：如图1，连接AC交BD于O，

∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵BE=DF，
∴OB+BE=OD+DF，即OE=OF，
∴四边形AFCE是平行四边形；
(2)解：∵四边形AFCE是平行四边形，AC⊥BD，即AC⊥EF，
∴四边形AFCE是菱形，
∴AF=CE=AE=CF，
故与AF相等的三条线段为AE、CE、CF. 
【解析】(1)连接AC交BD于O，根据平行四边形的判定与性质即可得到结论；
(2)根据菱形的判定与性质求解即可．
本题考查平行四边形的判定与性质、菱形的判定与性质，解答的关键是熟练掌握平行四边形和菱形的判定与性质．

19.【答案】解：(1)获得8分的学生的人数占抽取人数的百分数为：90∘360∘×100%=25%，
则剩余学生人数为：4+32+24=60(名)，占抽取人数的75%，
∴抽取学生的总人数为：60÷75%=80(名)，
∴获得8分的学生的人数为：80−60=20(名)，
补全频数分布直方图如下：

(2)估计该校初三学生获得10分学生的人数为：800×2580=250(名)；
(3)列表如下：

男1
男2
女
男1

男1男2
男1女
男2
男2男1

男2女
女
女男1
女男2

∵一共有6种等可能的结果，其中选中的两人均是男的情况共有2种等可能的结果，
∴P(选中的两人都是男生)=26=13. 
【解析】(1)求出抽取的总人数，即可解决问题；
(2)由初三学生总人数乘以获得10分学生的人数所占的比例即可；
(3)用列表法求出总的事件所发生的数目，再根据概率公式即可求出选中的这两人都是男生的概率．
本题考查的是用树状图法求概率以及条形统计图和扇形统计图．树状图法可以不重复不遗漏的列出所有可能的结果，适合两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．

20.【答案】解：(1)将点A(1,6)代入y=2x+b，可得2+b=6，即：b=4，
∴直线的解析式为：y=2x+4，
将点A(1,6)代入y=k1x，可得k11=6，即：k1=6，
∴双曲线的解析式为：y=6x；

(2)过点A，点B分别作AC⊥x轴，BD⊥x轴，则∠ACO=∠ODB=90∘，

∵A(1,6)，
∴AC=6，OC=1，
∵∠AOB=90∘，则∠AOC+∠BOD=∠BOD+∠OBD=90∘，
∴∠AOC=∠OBD，
又∵△ABO是等腰直角三角形，
∴AO=BO，
∴△AOC≌△OBD(AAS)，
∴OD=AC=6，BD=OC=1，
则B(6,−1)，
将点B(6,−1)代入y=k2x，可得k26=−1，即：k2=−6，
∴C2的解析式为y=−6x；

(3)作B关于x轴的对称点E，连接PA，PB，PE，可得E(6,1)，PE=PB，

则|PA−PB|=|PA−PE|≤AE，
当A，E，P在同一直线上时取等号，即此时|PA−PB|取最大值，亦即此时点P为直线AE与x的交点，
设直线AE解析式为：y=mx+n，将A(1,6)，E(6,1)代入，可得：
m+n=66m+n=1，
解得：m=−1n=7，
∴直线AE解析式为：y=−x+7，
当y=0时，−x+7=0，得x=7，
∴P(7,0). 
【解析】(1)利用待定系数法求解即可；
(2)过点A，点B分别作AC⊥x轴，BD⊥x轴，可证△AOC≌△OBD(AAS)，进而求得点B(6,−1)，再利用待定系数法求解即可；
(3)作B关于x轴的对称点E，连接PA，PB，PE可得E(6,1)，PE=PB，则|PA−PB|=|PA−PE|≤AE，当A，E，P在同一直线上时取等号，即此时|PA−PB|取最大值，亦即此时点P为直线AE与x的交点，利用待定系数法求得直线AE解析式为：y=−x+7，令y=0，求得得x=7，可得P(7,0).
本题考查待定系数法求解函数解析式，全等三角形的判定即性质，三角形的三边关系的应用，作出图形，利用数形结合是解决问题的关键．

21.【答案】(1)证明：∵DF平分∠ADE，
∴∠EDF=∠ADF，
∵∠ADF=∠ABC，∠BAC=∠BDC，∠EDF=∠BDC，
∴∠BAC=∠ABC，
∴AC=BC；
(2)解：∵BD是⊙O的直径，
∴AD⊥BF，
∵AF=AB，
∴DF=DB，
∴∠FDA=∠BDA，
∵∠ADB=∠ACB，∠ADF=∠ABC，
∴∠ACB=∠BAC=∠ABC，
∴△ACB是等边三角形，
∴∠ADB=∠ACB=60∘，
∴∠ABD=90∘−60∘=30∘，
∴∠F=∠ABD=30∘；
(3)解：∵CDAC=12，
∴CDBC=12，
设CD=k，k>0，则BC=2k，
∴BD= CD2+BC2= 5k=10，
∴k=2 5，
∴CD=2 5，BC=AC=4 5，
∵∠ADF=∠BAC，
∴∠FAC=∠ADC，
∵∠ACF=∠DCA，
∴△ACF∽△DCA，
∴CDAC=ACCF，
∴CF=8 5，
∴DF=CF−CD=6 5. 
【解析】本题综合考查了角平分线，相似三角形的判定和性质，圆内接四边形的性质，圆周角定理，熟知圆内接四边形的对角互补是解答此题的关键．
(1)根据角平分线的定义得到∠EDF=∠ADF，根据圆内接四边形的性质和圆周角定理结论得到结论；
(2)根据圆周角定理得到AD⊥BF，推出△ACB是等边三角形，得到∠ADB=∠ACB=60∘，根据等腰三角形的性质得到结论；
(3)设CD=k，k>0，则BC=2k，根据勾股定理得到BD= CD2+BC2= 5k=10，求得k=2 5，BC=AC=4 5，根据相似三角形的性质即可得到结论.

22.【答案】45 
【解析】解：(1)如图1，过点F作FH⊥直线BC于H，

∵AE⊥EF，FH⊥BC，
∴∠AEF=∠EHF=90∘=∠ABC，
∴∠AEB+∠FEC=90∘=∠AEB+∠BAE，
∴∠BAE=∠FEH，
又∵EF=AE，
∴△ABE≌△EHF(AAS)，
∴BE=FH，AB=EH，
∴BC=EH，
∴BE=CH=FH，
∴∠FCH=45∘，
∴∠DCF=45∘，
故答案为：45；
(2)EF=AE，理由如下：
如图2，过点E作EN⊥BC交AC于N，

∵四边形ABCD是正方形，
∴∠ACB=45∘=∠ACD=∠DCF，
∵NE⊥BC，AE⊥EP，
∴∠NEC=∠AEP=90∘，
∴∠AEN=∠PEC，∠ENC=∠ECN=45∘，
∴NE=EC，∠ANE=∠ECF=135∘，
∴△AEN≌△FEC(ASA)，
∴AE=EF；
(3)如图，连接AC，过点E作EN⊥BC交AC于N，

∵四边形ABCD是正方形，
∴∠ACB=45∘=∠ACD=∠DCF，
∵NE⊥BC，AE⊥EP，
∴∠NEC=∠AEP=90∘，
∴∠AEN=∠PEC，∠ENC=∠ECN=45∘，
∴NE=EC，∠ANE=135∘，
又∵AE=EF，
∴△AEN≌△FEC(ASA)，
∴∠ANE=∠ECF=135∘，
∴∠DCF=45∘，
∴点F是在过点C且与CD成45∘的直线上运动，
作点B关于CF的对称点B′，连接AB′，交CF于点F′，交BC于Q，连接BF′，
∴此时：AF+BF有最小值，最小值为AB′，
∵点B关于CF的对称点B′，
∴BC=B′C，∠BCF′=∠B′CF′=45，
∴∠BCB′=90∘，
∴B′C//AB，
∴ABB′C=BQCQ=1，
∴BQ=CQ=12，
∵∠BCF′=∠B′CF′=45，F′H⊥BC，F′G⊥B′C，
∴F′H=F′G，
∵S△B′CQ=12×1×12=12×12×F′H+12×1×F′G，
∴F′H=13，
∴△BCF的面积=12×13×1=16.
(1)由“AAS”可证△ABE≌△EHF，可得BE=FH，AB=EH，即可求解；
(2)由“ASA”可证△AEN≌△FEC，可得AE=EF；
(3)先证点F是在过点C且与CD成45∘的直线上运动，由面积法可求F′H的长，即可求解．
本题是四边形综合题，考查了正方形的性质，全等三角形的判定和性质，添加恰当辅助线构造全等三角形是解题的关键．

23.【答案】2+0.2x 
【解析】解：(1)市场价为每千克2元，每天上涨0.2元，存放x天后可上涨0.2x元，∴P=2+0.2x；
(2)根据题意列方程(200−x)(2+0.2x)=760
整理得：−0.2x2+38x+400=760，
解得：x1=10，x2=180，
故存放10天或180天；
(3)设利润为w，
W=(200−x)(2+0.2x)−20x−200×2=−0.2x2+18x=−0.2(x−45)2+405
当x=45天时，利润最大，最大利润是405元．
(1)根据市场价=原价+x天上涨的价格列出代数式；
(2)根据销售金额=x天后的市场价×可售葡萄的总质量列方程求解即可；
(3)根据利润=销售总金额−x天的总费用-成本，列出函数表达式，进而求得最值即可．
本题主要考查了二次函数的应用；理解销售总金额和利润的意义，得到销售总金额和总利润的等量关系是解决本题的关键．

24.【答案】解：(1)①将B(6,0)代入y=ax2+3x−6，
∴36a+18−6=0，
∴a=−13，
∴y=−13x2+3x−6，
∵直线y=x+b经过点B(6,0)，
∴6+b=0，
∴b=−6；

②作PM⊥x轴交于M，

∵y=−13x2+3x−6，
令x=0，则y=−6，即C(0,−6)，
令y=0，则−13x2+3x−6=0，
解得：x1=3，x2=6，
∴A(3,0)，
∴OA=3，OC=6，
设点P的横坐标为m，
∴P(m,−13m2+3m−6)，
∴PM=13m2−3m+6，AM=m−3，
∵△APC是以CP为斜边的直角三角形，
∴∠CAP=90∘，
∴∠OAC+∠PAM=90∘，
∵∠APM+∠PAM=90∘，
∴∠OAC=∠APM，
∵∠AOC=∠AMP=90∘，
∴△COA∽△AMP，
∴OAMP=OCMA，
∴OA⋅MA=OC⋅MP，
∴3(m−3)=6×(13m2−3m+6)，
整理得：2m2−21m+45=0，
解得：m1=152，m2=3(舍)
∴P(152,−94)；

(2)作PN⊥x轴交BC于N，过点N作NE⊥y轴于E，

设直线BC的解析式为y=kx+b0，由题意得：
6k+b0=0b0=−6，
解得：k=1b0=−6，
∴直线BC的解析式为y=x−6，
设点P的横坐标为m，则P(m,−13m2+3m−6)，N(m,m−6)，
∴PN=−13m2+3m−6−(m−6)=−13m2+2m，
∵PN⊥x轴，
∴PN//OC，
∴∠PNQ=∠OCB，
∵∠PQN=∠BOC=90∘，
∴Rt△PQN∽Rt△BOC，
∴PNBC=NQOC=PQOB，
∵OB=6，OC=6，
由勾股定理的：BC= OB2+OC2=6 2，
∴PN6 2=NQ6=PQ6，
∴NQ= 22PN，PQ= 22PN，
∴NQ=PQ= 22×(−13m2+2m)=− 26m2+ 2m，
∵∠CEN=∠BOC=90∘，∠ECN=∠OCB，
∴△CNE∽△CBO，
∴CNBC=ENOB，
∴CN6 2=m6，
∴CN= 2m，
∴CQ+PQ=CN+NQ+PQ
= 2m+(− 26m2+ 2m)+(− 26m2+ 2m)
=− 23m2+3 2m
=− 23(m2−9m)
=− 23(m−92)2+27 24，
当m=92时，CQ+PQ的最大值是27 24. 
【解析】(1)①把B(6,0)分别代入抛物线解析式和一次函数解析式求解，即可得到答案；
②作PM⊥x轴于点M，先求出C(0,−6)、A(3,0)，由题意可知P(m,−13m2+3m−6)，得到PM=13m2−3m+6，AM=m−3，再证明△COA∽△AMP，得到OAMP=OCMA，列方程求解，即可求出可m的值；
(2)作PN⊥x轴交BC于点N，过点N作NE⊥y轴于点E，先求出直线BC的解析式为y=x−6，设点P的横坐标为m，则P(m,−13m2+3m−6)，N(m,m−6)，得到PN=−13m2+2m，再证明Rt△PQN∽Rt△BOC，推出NQ=PQ= 22PN=− 26m2+ 2m，然后证明△CNE∽△CBO，推出CN= 2m，根据CQ+PQ得到关于m的二次函数，利用二次函数的性质求出最值，即可得到答案．
本题是二次函数的综合题，主要考查了二次函数的图象和性质，相似三角形的判定和性质，熟练掌握二次函数的图象和性质，相似三角形的判定和性质，利用数形结合思想解答是解题关键，是中考的压轴题．