2023年山东省德州市宁津县中考数学一模试卷(含答案解析)

这是一份2023年山东省德州市宁津县中考数学一模试卷(含答案解析)，共21页。试卷主要包含了5B等内容，欢迎下载使用。
2023年山东省德州市宁津县中考数学一模试卷1.  实数，0，，2中，为负数的是(    )A.  B. 0 C.  D. 22.  下列图形中，是轴对称图形的是(    )A.  B.  C.  D. 3.  2022年，温州市委、市政府决定发放新一轮消费券1200000000元，数据1200000000用科学记数法表示为(    )A.  B.  C.  D. 4.  如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A，B，C都在横线上．若线段，则线段BC的长是(    )A.
B. 1
C.
D. 3
 5.  下列算式，能按照“底数不变，指数相乘”计算的是(    )A.  B.  C.  D. 6.  如图是某校七年级二班参加课外兴趣小组人数的扇形统计图，根据图中信息，你认为哪一个兴趣小组参加人数最多的是(    )A. 唱歌
B. 绘画
C. 编程
D. 舞蹈7.  如图，数轴上A，B两点到原点的距离是三角形两边的长，则该三角形第三边长可能是(    )
 A.  B. 4 C. 7 D. 88.  如图，内接于，AD是的直径，若，则的度数是(    )
 A.  B.  C.  D. 9.  某校购买了一批篮球和足球．已知购买足球的数量是篮球的2倍，购买足球用了5000元，购买篮球用了4000元，篮球单价比足球贵30元．根据题意可列方程，则方程中x表示(    )A. 足球的单价 B. 篮球的单价 C. 足球的数量 D. 篮球的数量10.  当地时间2019年4月15日下午，法国巴黎圣母院发生火灾，大火烧毁了巴黎圣母院后塔的塔顶．烧毁前，为测量此塔顶B的高度，在地面选取了与塔底D共线的两点A、C，A、C在D的同侧，在A处测量塔顶B的仰角为，在C处测量塔顶B的仰角为，A到C的距离是米．设BD的长为x米，则下列关系式正确的是(    )A.  B.
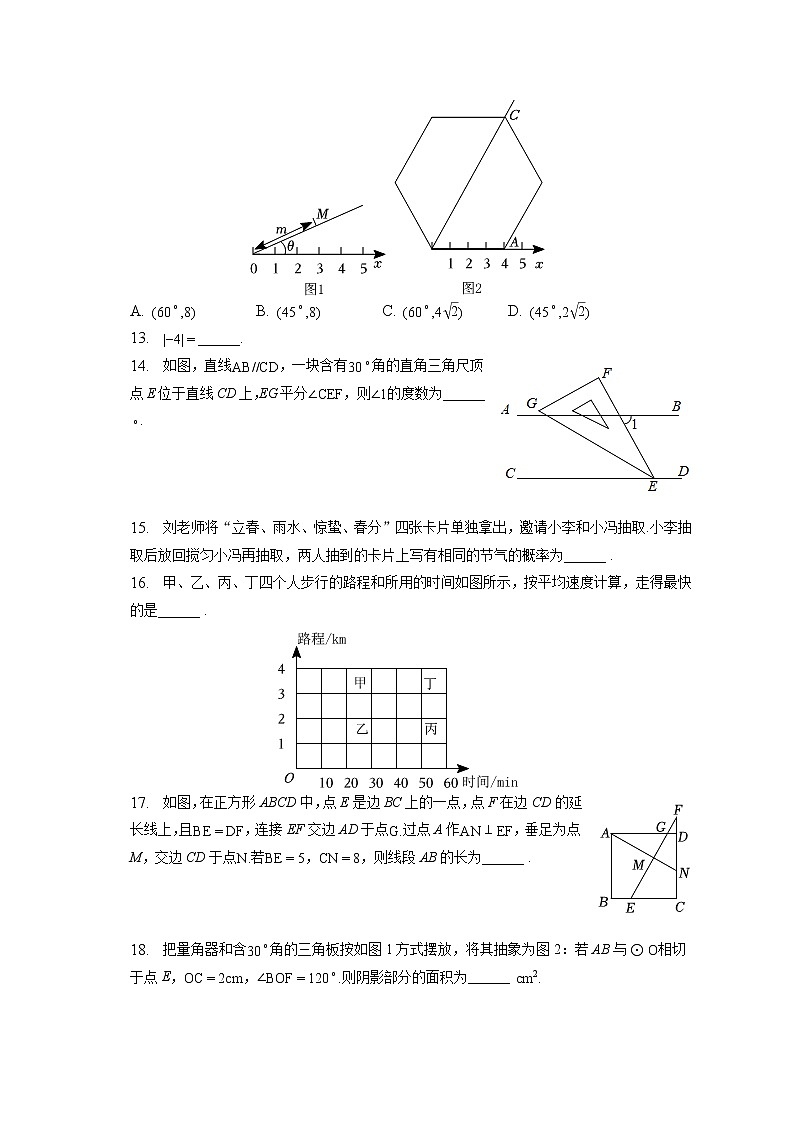
C.  D. 11.  已知函数的自变量x与函数值y之间满足下列表格中的数量关系，那么的值为(    )x245y3 A. 18 B. 15 C. 9 D. 312.  阅读理解：如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由的度数与OM的长度m确定，有序数对称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”.应用：在图2的极坐标系下，如果正六边形的边长为4，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为(    )
A.  B.  C.  D. 13.  ______.14.  如图，直线，一块含有角的直角三角尺顶点E位于直线CD上，EG平分，则的度数为______
 15.  刘老师将“立春、雨水、惊蛰、春分”四张卡片单独拿出，邀请小李和小冯抽取.小李抽取后放回搅匀小冯再抽取，两人抽到的卡片上写有相同的节气的概率为______ .16.  甲、乙、丙、丁四个人步行的路程和所用的时间如图所示，按平均速度计算，走得最快的是______ .
17.  如图，在正方形ABCD中，点E是边BC上的一点，点F在边CD的延长线上，且，连接EF交边AD于点过点A作，垂足为点M，交边CD于点若，，则线段AB的长为______ .
 18.  把量角器和含角的三角板按如图1方式摆放，将其抽象为图2：若AB与相切于点E，，则阴影部分的面积为______
 
 
 19.  解方程组：；
化简：20.  某校依据教育部印发的《大中小学劳动教育指导纲要试行》指导学生积极参加劳动教育，该校七年级数学兴趣小组利用课后托管服务时间，对七年级学生一周参加家庭劳动次数情况.开展了一次调查研究.①收集数据：通过问卷调查，兴趣小组获得了这20名学生每人一周参加家庭劳动的次数，数据如下：3 1 2 2 3 3 2 3 4 3 4 0 5 5 2 6
4 6 3；②整理、描述数据：整理数据，结果如下：分组频数21062③分析数据：平均数中位数众数a3根据以上信息，解答下列问题：
兴趣小组计划抽取该校七年级20名学生进行问卷调查，下面抽取方法中，合理的是______ ；
A.从该校七年级1班中随机抽取20名学生
B.从该校七年级女生中随机抽取20名学生
C.从该校七年级学生中随机抽取男、女各10名学生
补全频数分布直方图；
填空：______ ；
该校七年级现有400名学生，请估计该校七年级学生每周参加家庭劳动的次数达到平均水平及以上的学生人数；
21.  如图是海洋公园娱乐设施“水上滑梯”的侧面图，建立如图坐标系．其中BC段可看成是反比例函数图象的一段，矩形AOEB为向上攀爬的梯子，梯子高6米，宽1米，出口C点到BE的距离CF为11米，求：
段所在的反比例函数关系式是什么？
点到x轴的距离CD长是多少？
若滑梯BC上有一个小球Q，Q的高度不高于3米，则Q到BE的距离至少多少米？
22.  如图，已知
用尺规作图：作线段AB的垂直平分线，垂足为D，交AM于点C，连接BC；作的平分线CN，在CN上截取，连接BE；
求证：中所作的四边形BDCE是矩形.
23.  翻开史书，中华文化灿烂的历史展现在眼前，尤其是红色革命文化的精神，值得人们传承和弘扬，一部部红色典籍更是每个时代都需要的精神食粮.某学校计划开设阅读课让同学们学习革命文化，便购买了《红岩》和《林海雪原》供学生阅读，首次购买书籍的单价及花费如表： 《红岩》《林海雪原》单价元/本x购买花费元675540已知首次购买到的两种书籍数量相等.
求学校购买的两种书籍的单价各为多少元？
首次购书之后，学校发现学生对革命文化有了更深入的了解，现打算再次购买500本，这一次学校共花费6600元，那么这次购买《林海雪原》多少本？24.  [概念引入]
在一个圆中，圆心到该圆的任意一条弦的距离，叫做这条弦的弦心距．
[概念理解]
如图1，在中，半径是5，弦，则这条弦的弦心距OC长为______.
通过大量的做题探究；小明发现：在同一个圆中，如果两条弦相等，那么这两条弦的弦心距也相等．但是小明想证明时却遇到了麻烦．请结合图2帮助小明完成证明过程如图2，在中，，，，求证：
[概念应用]如图3，在中，的直径为20，且弦AB垂直于弦CD于E，请应用上面得出的结论求OE的长．
 25.  根据以下素材，探索完成任务.如何设计喷水池喷头的安装方案？素材1图1中有一个直径为20m的圆形喷水池，四周安装一圈喷头，喷射水柱呈抛物线型，在水池中心O处立着一个直径为1m的圆柱形实心石柱，各方向喷出的水柱在石柱顶部的中心点M处汇合，如图2，水柱距水池中心4m处到达最高，高度为素材2如图3，拟在水池里过水池中心的直线上安装一排直线型喷头喷射水柱竖直向上，高度均为；相邻两个直线型喷头的间距均为，且喷射的水柱不能碰到抛物线型水柱，要求在符合条件处都安装喷头，安装后关于OM成轴对称分布.问题解决任务1确定水柱形状在图2中建立合适的直角坐标系，任选一条抛物线求函数表达式.任务2确定石柱高度在你所建立的坐标系中，确定水柱汇合点M的纵坐标.任务3拟定设计方案请给出符合所有要求的直线型喷头的安装数量，并根据你所建立的直角坐标系，求出离中心O最远的两个直线型喷头的坐标.
答案和解析 1.【答案】A 【解析】解：
负数是：，
故选
根据负数的定义，找出这四个数中的负数即可．
本题主要考查实数的分类，区分正负，解题的关键是熟知实数的性质：负数小于零．
 2.【答案】B 【解析】解：选项A、C、D不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，
选项B能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，
故选：
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
 3.【答案】C 【解析】解：
故选：
科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值时，n是正整数；当原数的绝对值时，n是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，n为整数，表示时关键要正确确定a的值以及n的值．
 4.【答案】C 【解析】解：过点A作平行横线的垂线，交点B所在的平行横线于D，交点C所在的平行横线于E，

则，即，
解得：，
故选：
过点A作平行横线的垂线，交点B所在的平行横线于D，交点C所在的平行横线于E，根据平行线分线段成比例定理列出比例式，计算即可．
本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．
 5.【答案】C 【解析】解：能按照“底数不变，指数相乘”计算的是
故选：
直接利用同底数幂的乘除运算、幂的乘方运算法则判断得出答案．
此题主要考查了幂的乘方运算、同底数幂的乘除运算，正确掌握相关运算法则是解题关键．
 6.【答案】A 【解析】解：由扇形统计图可以看出，编程占的百分比为，
所以唱歌占的百分比为
所以唱歌的参加人数最多．
故选：
求出所占比例最多的就是兴趣小组参加人数最多的．
本题主要考查对于扇形统计图的应用以及数据的计算．
 7.【答案】B 【解析】解：由题意知，该三角形的两边长分别为3、
不妨设第三边长为a，则，即
观察选项，只有选项B符合题意．
故选：
由实数与数轴与绝对值知识可知该三角形的两边长分别为3、然后由三角形三边关系解答．
本题主要考查了三角形三边关系，绝对值，实数与数轴，要注意三角形形成的条件：任意两边之和>第三边，任意两边之差<第三边，
 8.【答案】C 【解析】解：连接BD，

是的直径，
，
，
，
，
故选：
连接BD，根据直径所对的圆周角是直角可得，从而可求出的度数，然后利用同弧所对的圆周角相等即可解答．
本题考查了圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
 9.【答案】D 【解析】解：设篮球的数量为x个，足球的数量是2x个．
根据题意可得：，
故选：
设篮球的数量为x个，足球的数量是2x个，列出分式方程解答即可．
此题主要考查了由实际问题抽象出分式方程，得到相应的关系式是解决本题的关键．
 10.【答案】A 【解析】【分析】
本题考查了解直角三角形的应用-仰角俯角问题，要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．
根据三角函数得出，进而利用根据可得答案．
【解答】
解：在A处测量塔顶B的仰角为，在C处测量塔顶B的仰角为，A到C的距离是米．设BD的长为x米，
可得：，
故选：  11.【答案】A 【解析】解：抛物线经过，，
抛物线对称轴为直线，
，
抛物线经过，对称轴为直线，
抛物线经过，即，
，
故选：
由抛物线经过，可得抛物线的对称轴，从而可得的值，再由抛物线的对称性及点可得的值，进而求解．
本题考查二次函数的性质，解题关键是掌握二次函数图象与系数的关系，掌握二次函数与方程的关系．
 12.【答案】A 【解析】解：如图，设正六边形的中心为D，连接AD，
，，
是等边三角形，
，，
，
正六边形的顶点C的极坐标应记为
故选：
设正六边形的中心为D，连接AD，判断出是等边三角形，根据等边三角形的性质可得，，再求出OC，然后根据“极坐标”的定义写出即可．
本题考查了正多边形和圆，坐标确定位置，主要利用了正六边形的性质，读懂题目信息，理解“极坐标”的定义是解题的关键．
 13.【答案】4 【解析】【分析】
本题考查绝对值，正数的绝对值是其本身，负数的绝对值是它的相反数，0的绝对值是因为，由绝对值的性质，可得的值.
【解答】
解：
故答案为  14.【答案】60 【解析】解：，
，
平分，，
，
，
故答案为
根据两直线平行，可以得出内错角相等，，由EG平分，角平分线的性质得，，故可以得出的度数．
本题考查平行线的性质和角平分线，解本题要熟练掌握平行线的性质和角平分线．
 15.【答案】 【解析】解：设立春、雨水、惊蛰、春分分别记为A，B，C，D，
画树状图如下：

共有16种等可能的结果，其中两人抽到的卡片上写有相同的节气的结果有4种，
两人抽到的卡片上写有相同的节气的概率为
故答案为：
画树状图得出所有等可能的结果数以及两人抽到的卡片上写有相同的节气的结果数，再利用概率公式可得出答案．
本题考查列表法与树状图法，熟练掌握列表法与树状图法以及概率公式是解答本题的关键．
 16.【答案】甲 【解析】解：分钟甲比乙步行的路程多，25分钟丁比丙步行的路程多，
甲的平均速度>乙的平均速度，丁的平均速度>丙的平均速度，
步行3千米时，乙比丙用的时间少，
乙的平均速度>丙的平均速度，
走得最快的是甲，
故答案为：甲．
当时间一样的时候，分别比较甲、乙和丙、丁的平均速度；当路程都是3千米的时候，比较甲、丁的平均速度即可得出答案．
本题考查了函数的图象，通过控制变量法比较平均速度的大小是解题的关键．
 17.【答案】20 【解析】解：如图，连接AE，AF，EN，

四边形ABCD为正方形，
，，，
在和中，
，
≌，
，，
，
为等腰直角三角形，
，
，，
≌，≌，
，
设，
，，
，
，，
在中，由勾股定理可得：
，
即，
解得：，
，

故答案为：
连接AE，AF，EN，由正方形的性质可得，，，可证得≌，可得，，从而可得，根据等腰三角形三线合一可得点M为EF中点，由可证得≌，≌，可得，设，则，，由勾股定理解得，可得，
本题考查正方形的性质，勾股定理，等腰三角形的性质，全等三角形的判定与性质等知识点，解题的关键是正确作出辅助线，构建全等三角形解决问题．
 18.【答案】 【解析】解：连接OE，
与半圆相切于E，
半径，
，
，
，
，
，
，
，
 ，
的面积，
，
扇形DOE的面积，
阴影的面积的面积-扇形DOE的面积
故答案为：
连接OE，由切线的性质得到，，由，得到，求出OF的长，即可求出BE的长，从而求出的面积，扇形DOE的面积，即可得到阴影的面积．
本题考查切线的性质，扇形面积的计算，关键是掌握切线的性质，扇形面积计算公式．
 19.【答案】解：①+②，得，
解得，
将代入②，得，
所以，方程组的解为：；
原式



 【解析】先用加减消元法求出x的值，再用代入消元法求出y的值即可；
根据分式混合运算的法则进行计算即可．
本题考查的是分式的混合运算及解二元一次方程组，熟知分式混合运算的法则是解题的关键．
 20.【答案】C 3 【解析】解：兴趣小组计划抽取该校七年级20名学生进行问卷调查，下面的抽取方法中，合理的是从该校七年级学生中随机抽取男，女各10名学生；
故答案为：C；
补全频数分布直方图：

被抽取的20名学生每人一周参加家庭劳动的次数从小到大排列，排在中间的两个数分别为3、3，故中位数；
故答案为：3；
由题意可知，被抽取的20名学生中达到平均水平及以上的学生人数有8人，
人，
答：估计该校七年级学生每周参加家庭劳动的次数达到平均水平及以上的学生有160人；
根据抽样调查的可靠性即可得出答案；
根据频数分布表中的数据即可补全频数分布直方图；
根据中位数的定义即可得出答案；
用400乘以平均水平及以上的百分比即可．
本题考查抽样调查的可靠性、频数分布直方图、中位数、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．
 21.【答案】解：四边形AOEB是矩形，
，，
，
设双曲线BC的解析式为，
，
段所在的反比例函数关系式是；
，
点C的横坐标为12，
当时，，
长为米；
的高度不高于3米，即，
，
解得，
，
到BE的距离至少1米， 【解析】根据矩形的性质得到，，求得，设双曲线BC的解析式为，得到，于是得到结论；
根据题意写出点C的横坐标，然后代入中解析式求出y即可；
令，解出x的取值范围即可．
本题考查了反比例函数的应用，矩形的性质，掌握的识别图形是解题的关键．
 22.【答案】解：作法：分别以点A、B为圆心，大于长为半径作弧，交于点P、Q；
过点P、Q作直线交AB于点D，交AM于点C；
连接BC；
以点C为圆心，任意长为半径作弧，分别交CM、CB于点G、H；
分别以点G、H为圆心，大于长为半径作弧，两弧在内部交于点N；
作射线CN；
在CN上截取；
连接
证明：的垂直平分线PQ交AAB于点D，交AM于点C，
，，
，
，
，
平分，
，
，
，
，
，
，
四边形BDCE是平行四边形，
，
四边形BDCE是矩形． 【解析】用圆规和直尺按作一条线段等于已知线段、作已知线段的垂直平分线、作已知角的平分线的作法作出图形并保留作图痕迹即可；
由线段的垂直平分线的性质得，则，可推导出，由CN平分，得，则，所以，由，，得，则四边形BDCE是平行四边形，再由，根据矩形的定义证明四边形BDCE是矩形即可．
此题重点考查尺规作图、作一条线段等于已知线段、作已知线段的垂直平分线、作已知角的平分线等基本作图、线段的垂直平分线的性质、等腰三角形的性质、矩形的判定等知识，熟练掌握有关基本作图的作法是解题的关键．
 23.【答案】解：由题知，学校购买《红岩》的单价为x元/本，
购买《林海雪原》的单价为元/本，，
根据题意，得：，
解得，
经检验，是原分式方程的解，且符合题意，
元/本
答：学校购买《红岩》的单价为15元/本，《林海雪原》的单价为12元/本；

设购买《林海雪原》m本，，则购买《红岩》本，
根据题意，得：，
解得
答：这次购买《林海雪原》300本． 【解析】根据表中数据列出分式方程，解方程并检验结果即可；
设购买《林海雪原》m本，根据题意列方程求解即可．
本题主要考查了分式方程的应用和一元一次方程的应用，解答本题的关键是找准等量关系，列出方程．
 24.【答案】3 【解析】[概念理解解：连接OB，
，
，，
，
，
，
，
故答案为：3；  
证明：连接BO、OC，
，
，，
，
，，
，
，
，
，
；
[概念应用]解：过点O作交于G，过点O作交于H，连接DO，
，
，
，
，
四边形GEHO是正方形，
，
，
，
的直径为20，
，
，
，

[概念理解连接OB，在中，应用勾股定理求解即可；
连接BO、OC，证明即可；
[概念应用]过点O作交于G，过点O作交于H，连接DO，根据的结论，得到四边形GEHO是正方形，在中，用勾股定理求出，在等腰中，求出
本题考查圆的综合应用，熟练掌握垂径定理，勾股定理，三角形全等的判定及性质，正方形的性质是解题的关键．
 25.【答案】解：【任务1】以点O为原点建立如图所示直角坐标系，选择第一象限内的抛物线的解析式进行求解，

根据题意，设，
将点代入抛物线，解得
抛物线的解析式为：
【任务2】，
将代入，可得
点M的纵坐标为
【任务3】如图，令，
解得或舍，
安装后关于OM成轴对称分布，石柱直径为1，，，

左右两侧各安装7个直线型喷头，共14个喷头，
离中心O最远的两个喷头的坐标分别为， 【解析】【任务1】以点O为原点建立如图所示直角坐标系，选择第一象限内的抛物线的解析式进行求解，设出抛物线的顶点式，再将代入即可得出结论；
【任务2】令上述抛物线，即可得出结论；
【任务3】令上述抛物线，可求出x的值，再根据对称性可分别求出两端的喷头坐标．
本题考查了二次函数在实际问题中的应用，理清题中的数量关系、熟练掌握待定系数法及二次函数的性质是解题的关键．