初中数学湘教版九年级上册2.4 一元二次方程根与系数的关系一等奖ppt课件

这是一份初中数学湘教版九年级上册2.4 一元二次方程根与系数的关系一等奖ppt课件，共16页。PPT课件主要包含了探究新知，x1+x2-3，x1·x2-4，x1+x25，x1·x26，猜一猜，证一证，b2-4ac≥0，韦达定理，针对训练等内容，欢迎下载使用。

创设情境 新课导入
一元二次方程ax2+bx+c = 0(a≠0)的根的值由方程的系数a，b，c来决定，除此之外,根与系数之间还有什么关系呢？
1、一元二次方程的根的判别式
2、方程根的判别方法
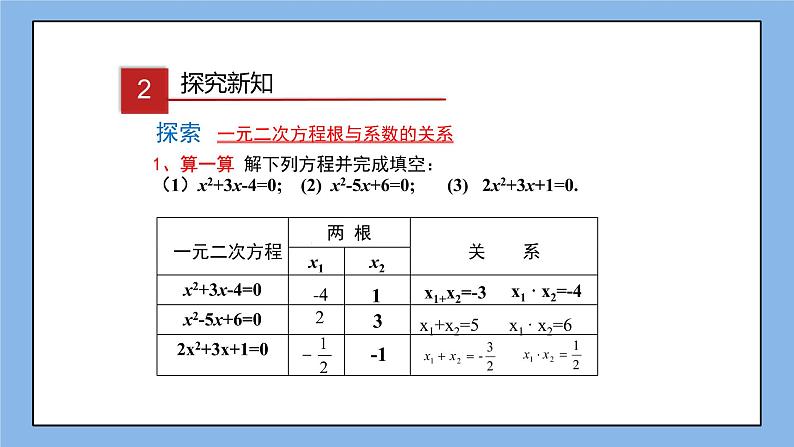
1、算一算 解下列方程并完成填空：（1）x2+3x-4=0; (2) x2-5x+6=0; (3) 2x2+3x+1=0.
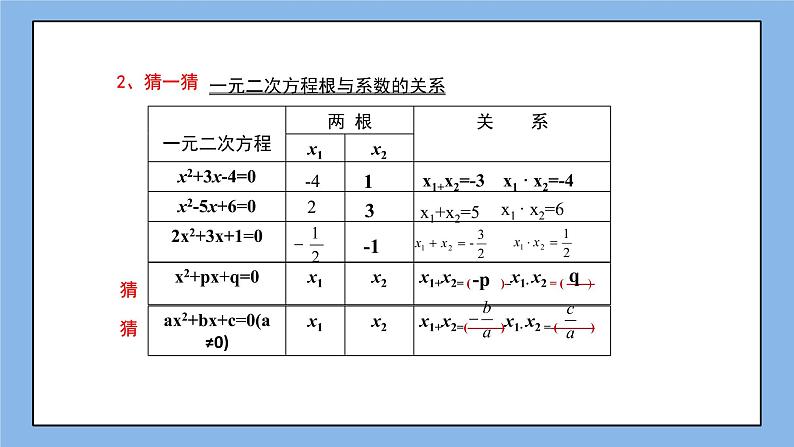
一元二次方程根与系数的关系
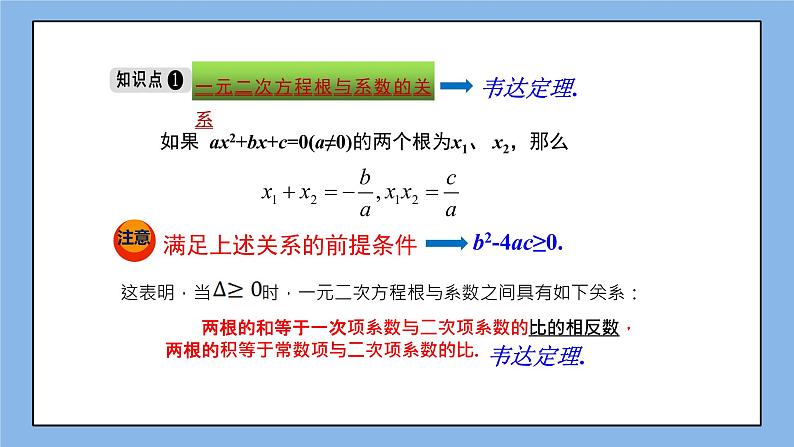
如果 ax2+bx+c=0(a≠0)的两个根为x1、 x2，那么
满足上述关系的前提条件
两根的和等于一次项系数与二次项系数的比的相反数，两根的积等于常数项与二次项系数的比.
例1：利用根与系数的关系，求下列方程的两根之和、两根之积. （1）x2 + 7x + 6 = 0;
解：这里 a = 1 , b = 7 , c = 6. Δ = b2 - 4ac = 72 – 4 × 1 × 6 = 25 > 0. ∴方程有两个实数根. 设方程的两个实数根是 x1, x2, 那么 x1 + x2 = -7 , x1 x2 = 6.
一元二次方程根与系数的关系的应用
（2）2x2 - 3x - 2 = 0.
解：这里 a = 2 , b = -3 , c = -2. Δ= b2 - 4ac = （- 3）2 – 4 × 2 × (-2) = 25 > 0, ∴方程有两个实数根. 设方程的两个实数根是 x1, x2, 那么 x1 + x2 = , x1 x2 = -1 .
例2 已知方程5x2+kx-6=0的一个根是2，求它的另一个根及k的值.
解：设方程的两个根分别是x1、x2，其中x1=2 . 所以：x1 · x2=2x2= 即：x2= 由于x1+x2=2+ = 得：k=－7.答：方程的另一个根是 ，k=－7.
变式：已知方程3x2-18x+m=0的一个根是1，求它的另一个根及m的值.
解：设方程的两个根分别是x1、x2，其中x1=1. 所以：x1 + x2=1+x2=6， 即：x2=5 . 由于x1·x2=1×5= 得：m=15.答：方程的另一个根是5，m=15.
例3 不解方程，求方程2x2+3x-1=0的两根的平方和、倒数和.
解：根据根与系数的关系可知：
例4 设x1，x2是方程 x2 -2(k - 1)x + k2 =0 的两个实数根， 且x12 +x22 =4，求k的值.
解：由方程有两个实数根，得Δ= 4（k - 1）2 - 4k2 ≥ 0 即 -8k + 4 ≥ 0. 由根与系数的关系得 x1 + x2 = 2(k -1) , x1 x2 =k 2. ∴ x12 + x22 = (x1 + x2)2 - 2x1x2 = 4(k -1)2 -2k2 = 2k2 -8k + 4. 由 x12 + x22 = 4，得 2k2 - 8k + 4 = 4, 解得 k1= 0 , k2 = 4 . 经检验， k2 = 4 不合题意，舍去.
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
一元二次方程的根与系数的关系的应用