数学3.4 相似三角形的判定与性质优质ppt课件

这是一份数学3.4 相似三角形的判定与性质优质ppt课件，共12页。

创设情境 新课导入
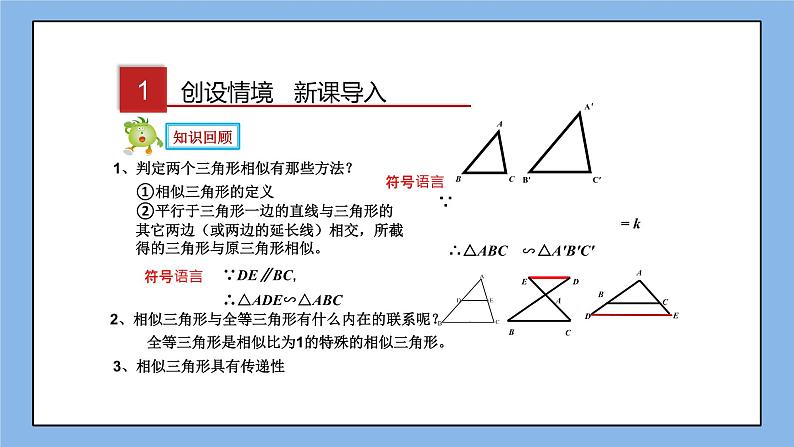
1、判定两个三角形相似有那些方法？
②平行于三角形一边的直线与三角形的其它两边（或两边的延长线）相交，所截得的三角形与原三角形相似。
2、相似三角形与全等三角形有什么内在的联系呢？
全等三角形是相似比为1的特殊的相似三角形。
3、相似三角形具有传递性
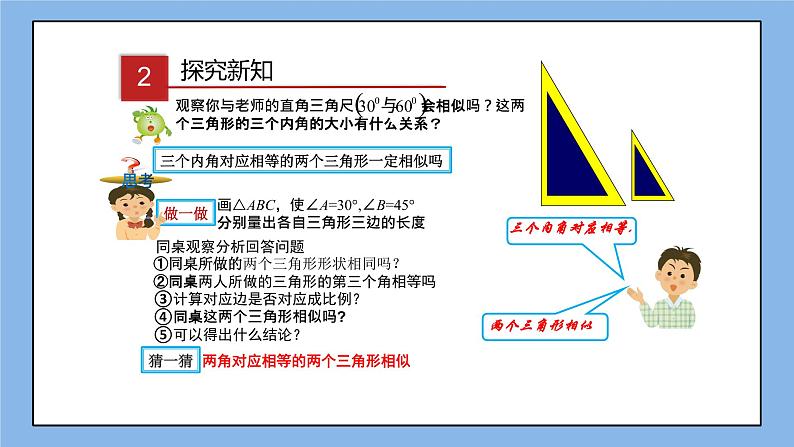
三个内角对应相等的两个三角形一定相似吗
同桌观察分析回答问题 ①同桌所做的两个三角形形状相同吗？ ②同桌两人所做的三角形的第三个角相等吗 ③计算对应边是否对应成比例？ ④同桌这两个三角形相似吗? ⑤可以得出什么结论？
画△ABC，使∠A=30°,∠B=45°分别量出各自三角形三边的长度
两角对应相等的两个三角形相似
已知：在△ABC和△A′B′C′中，∠A=∠A′，∠B=∠B′. 求证：△ABC∽△A′B′C′.
∵A′D=AB，∠A=∠A′，A′E=AC，
证明：在△A′B′C′的边A′B′、A′C′上，分别截取A′D=AB，A′E=AC，连接DE.
∴△A′DE≌△ABC， ∴∠A′DE=∠B，
又∵∠B′=∠B， ∴∠A′DE=∠B′，
∴DE∥B′C′，
∴△A′B′C′∽△ABC
∴△A′DE∽△A′B′C′，
即：两角分别相等的两个三角形相似
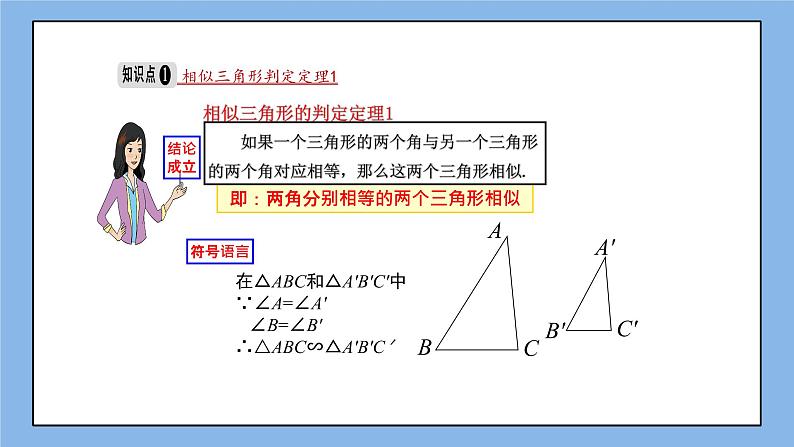
如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似.
相似三角形判定定理1
在△ABC和△A′B′C′中∵∠A=∠A′ ∠B=∠B′ ∴△ABC∽△A′B′C′
相似三角形的判定定理1
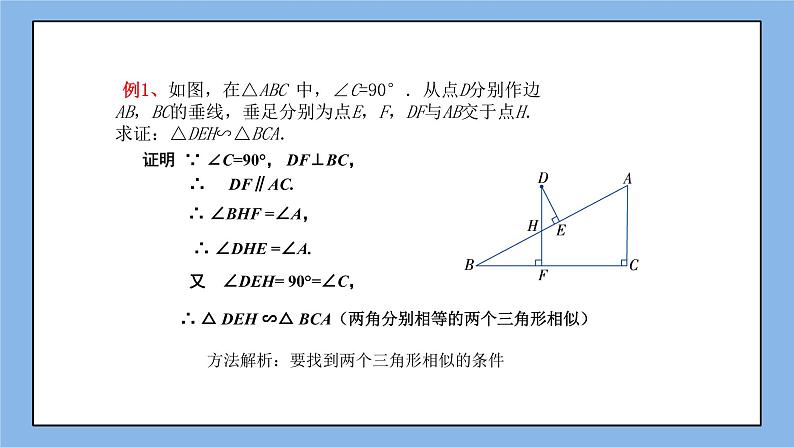
例1、如图，在△ABC 中，∠C=90°．从点D分别作边AB，BC的垂线，垂足分别为点E，F，DF与AB交于点H．求证：△DEH∽△BCA．
证明 ∵ ∠C=90°， DF⊥BC，
∴ ∠BHF =∠A，
∴ ∠DHE =∠A.
又 ∠DEH= 90°=∠C，
∴ △ DEH ∽△ BCA（两角分别相等的两个三角形相似）
方法解析：要找到两个三角形相似的条件
例2、如图，在Rt△ABC 与Rt△DEF中，∠C=90°， ∠F = 90°． 若∠A =∠D，AB = 5，BC = 4，DE = 3，求EF的长．
∴ EF = 2.4.
∴ △ABC ∽△DEF.
又 AB = 5，BC = 4，DE = 3，
【类型一】利用相似三角形的判定定理1求值
方法总结：根据三角形内角和可判定∠ACB＝∠CED，再结合相似三角形判定定理1得出△ABC与△CDE的相似关系，从而求解.
例3、 如图，已知AB⊥BD，ED⊥BD，AC⊥CE，点B，D，C分别为垂足，点C是线段BD的中点，若ED＝1，BD＝4，则AB＝　　　　.
又∵ED＝1，BD＝4，C为BD的中点
例4、如图所示，在△ABC中，∠AED＝∠B，则下列等式成立的是（　　）
解析：由相似三角形的判定定理1可得△ADE∽△ACB，即可得 ，故选C.
方法总结：在解此题时一定要明确对应关系， 由于△ADE∽△ACB， 所以AE对应AB，AD对应AC，ED对应BC.
【类型二】利用相似三角形的判定定理1证明相似
　　方法总结：解此类题型时首先要根据题设寻求两三角形相似的条件，再证明两三角形相似，并根据相似获得题目要求的数量关系.
例5、如图，在△ABC中，AB＝AC，BD＝CD，CE⊥AB于E. 求证：△ABD∽△CBE. 解析：已知∠B是公共角，判定两三角形相似， 再找一组角相等即可， 由题易证AD⊥BC，有∠ADB＝∠CEB＝90°，即可得证. 证明：在△ABC中， AB＝AC， BD＝CD， ∴AD⊥BC， ∵CE⊥AB， ∴∠ADB＝∠CEB＝90°， 又∠B＝∠B， ∴△ABD∽△CBE.
相似三角形的判定定理1
内容：两角分别相等的两个三角形相似
相似三角形判定定理1的运用