数学九年级上册第3章 图形的相似3.4 相似三角形的判定与性质试讲课课件ppt

这是一份数学九年级上册第3章 图形的相似3.4 相似三角形的判定与性质试讲课课件ppt，共15页。PPT课件主要包含了探究1，探究2，等于相似比，CD240m等内容，欢迎下载使用。

创设情境 新课导入
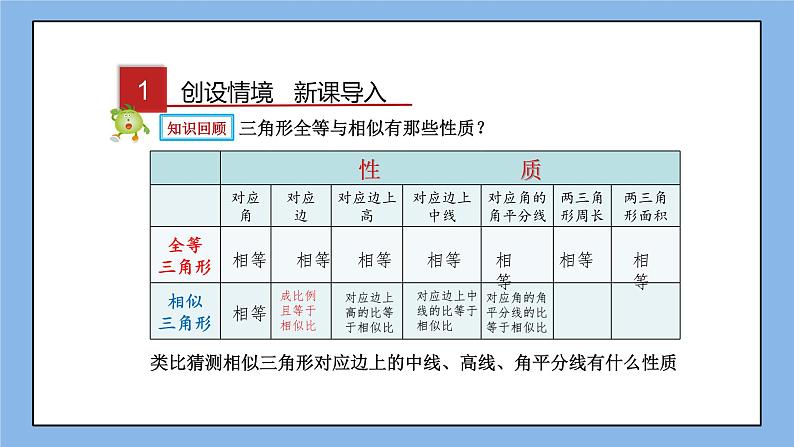
三角形全等与相似有那些性质？
类比猜测相似三角形对应边上的中线、高线、角平分线有什么性质
对应边上高的比等于相似比
对应边上中线的比等于相似比
对应角的角平分线的比等于相似比
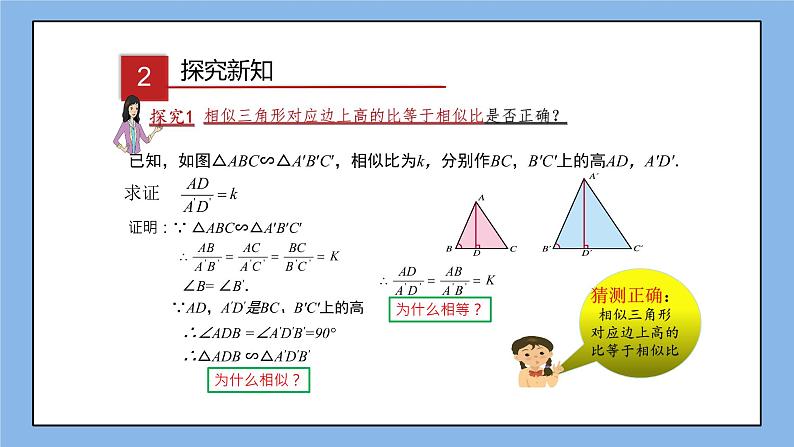
相似三角形对应边上高的比等于相似比是否正确？
已知，如图△ABC∽△A′B′C′，相似比为k，分别作BC，B′C′上的高AD，A′D′．
证明：∵ △ABC∽△A′B′C′
∴△ADB ∽△A'D'B'
∵AD，A'D'是BC、B′C′上的高
∴∠ADB =∠A'D'B'=90°
相似三角形的对应边上高的比等于相似比
类似的，我们可以证明其余两组对应边上的高的比也等于相似比．
若把相似三角形对应边上的高改为对应角的角平分线、对应边上的中线，那么它们对应角平分线的比、对应中线的比等于多少？
你能用仿照对应边的上高的比等于相似比的方法证明吗
那大家就仿照相似三角形对应高的比等于相似比方法证一证
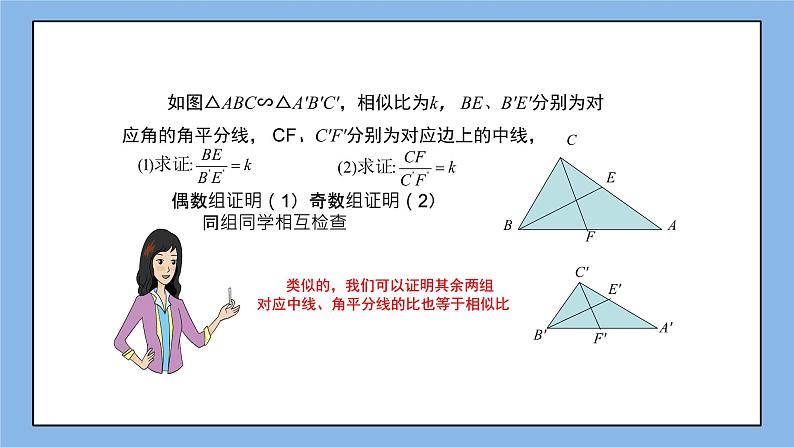
如图△ABC∽△A′B′C′，相似比为k， BE、B′E′分别为对应角的角平分线， CF、C′F′分别为对应边上的中线，
偶数组证明（1）奇数组证明（2） 同组同学相互检查
类似的，我们可以证明其余两组对应中线、角平分线的比也等于相似比
相似三角形的对应边上中线的比等于相似比
相似三角形的对应角的角平分组的比等于相似比
若△ABC∽△A′B′C′，相似比为k， AD、A′D′分别为对应边上的高，BE、B′E′，分别为对应角的角平分线， CF、C′F′分别为对应边上的中线，那么AD、A′D′，BE、B′E′，CF、C′F′之间有什么关系。
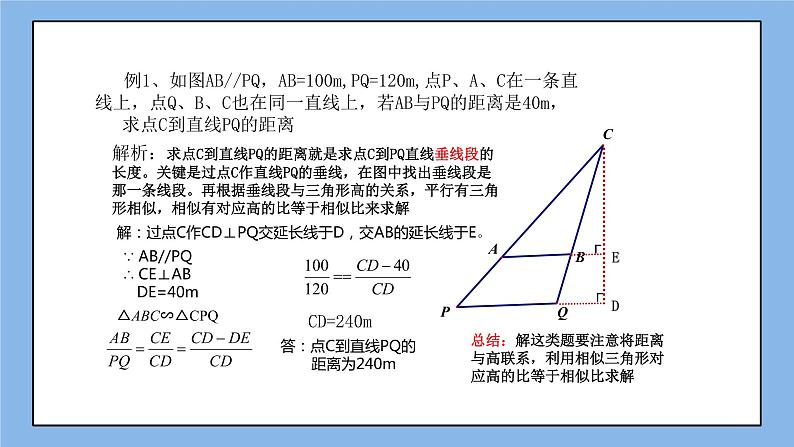
例1、如图AB//PQ，AB=100m,PQ=120m,点P、A、C在一条直线上，点Q、B、C也在同一直线上，若AB与PQ的距离是40m， 求点C到直线PQ的距离
解析：求点C到直线PQ的距离就是求点C到PQ直线垂线段的长度。关键是过点C作直线PQ的垂线，在图中找出垂线段是那一条线段。再根据垂线段与三角形高的关系，平行有三角形相似，相似有对应高的比等于相似比来求解
解：过点C作CD⊥PQ交延长线于D，交AB的延长线于E。
∵ AB//PQ∴ CE⊥AB DE=40m
答：点C到直线PQ的 距离为240m
总结：解这类题要注意将距离与高联系，利用相似三角形对应高的比等于相似比求解
例2、如图，AD是ΔABC的高，点P，Q在BC边上，点R在AC边上，点S在AB边上，BC=60cm，AD=40cm，四边形PQRS是正方形.
(1)AE是Δ ASR的高吗？为什么？
(2) ΔASR与ΔABC相似吗？为什么？
(3)求正方形PQRS的边长.
（1）解： AE是ΔASR的高. 理由： ∵AD是ΔABC的高 ∴ ∠ADC=90° ∵四边形PQRS是正方形 ∴SR∥BC ∴∠AER=∠ADC=90° ∴ AE是ΔASR的高.
总结：理解高是垂线段，只有两直线垂直即交角为90°时，才有垂线段。
（2）解： ΔASR与ΔABC相似. 理由: ∵ SR∥BC ∴ ΔASR与ΔABC相似.
（3）解：∵ ΔASR ∽ ΔABC AE、AD分别是ΔASR 和ΔABC 对应边上的高 ∴ 设正方形PQRS的边长为 x cm, 则SR=DE=x cm,AE=(40-x)cm ∴ ∴正方形PQRS的边长为24cm.
总结：利用相似三角形的对应边上高的比等于相似比和正方形的四边都相等是解决问题的关键。设正方形的边长为x能使问题变得简单。
思考：如图，AD是ΔABC的高，点P，Q在BC边上，点R在AC边上，点S在AB边上，BC=5cm，AD=10cm，若矩形PQRS的长是宽的2倍，你能求出这个矩形的面积吗？
设SP=xcm，则SR=2x cm 得到 : x=2 2x=4 S矩形PQRS= 2×4=8cm2
∵ ΔASR ∽ ΔABC
设SR=xcm，则SP=2x cm
所以 x=2.5 2x=5S矩形PQRS=2.5×5=12.5cm2
总结：由于长和宽的不确定性，所以要分情况进行讨论。再利用相似三角形的性质求解
解析：由于矩形的长与宽不确定性， 要分情况进行讨论。
例3、如图所示，已知△ABC∽△A′B′C′，AD，BE分别是△ABC的高和中线，A′D′，B′E′分别是△A′B′C′的高和中线，求证：AD·B′E′＝BE·A′D′.
解析：由△ABC∽△A′B′C′，可以对应高与对应中线的比都等于相似比，即可得证.证明：∵△ABC∽△A′B′C′，设△ABC和△A′B′C′的相似比为k，∵AD，BE分别是△ABC的高和中线，A′D′，B′E′分别是△A′B′C′的高和中线，∴∴AD·B′E′＝BE·A′D′.
类型一：相似三角形的对应中线、对应高、对应角平分线的比等于相似比
方法总结：本题考查相似三角形对应高和中线的性质，解题时应从三角形的相似出发，寻找对应的比例关系解题.
2、ΔABC∽ ΔA1B1C1 ，BD和B1D1是它们的中线， 已知 B1D1 =4cm，则BD= cm.
3、ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分 线，已知AD=8cm，A1D1=3cm , 则 ΔABC与 ΔA1B1C1的对应高之比为 .
4、如图、电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB=2m， CD=4m，点P到CD的距离是3m，则P到AB的距离是 m.
三角形对应边上中线的比等于相似比
相似三角形对应角的角平分线的比等于相似比
三角形对应边上高的比等于相似比