



数学湘教版3.5 相似三角形的应用试讲课ppt课件
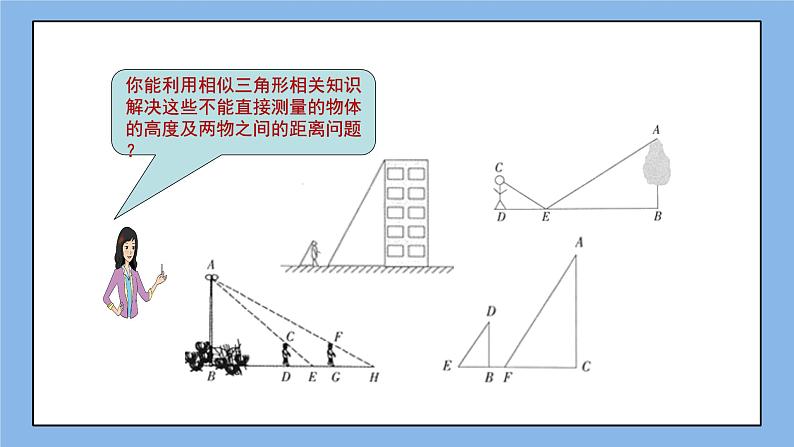
展开创设情境 新课导入
世界上最高的树 —— 红杉
世界上最宽的河 ——亚马逊河
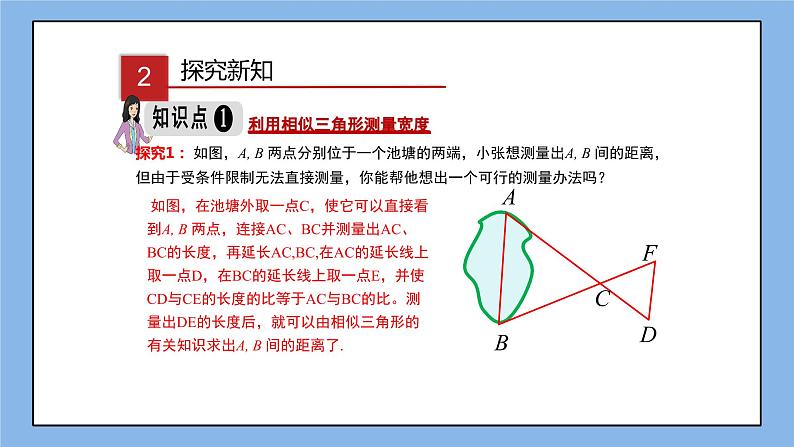
探究1: 如图,A, B 两点分别位于一个池塘的两端,小张想测量出A, B 间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量办法吗?
利用相似三角形测量宽度
如图,在池塘外取一点C,使它可以直接看到A, B 两点,连接AC、BC并测量出AC、BC的长度,再延长AC,BC,在AC的延长线上取一点D,在BC的延长线上取一点E,并使CD与CE的长度的比等于AC与BC的比。测量出DE的长度后,就可以由相似三角形的有关知识求出A, B 间的距离了.
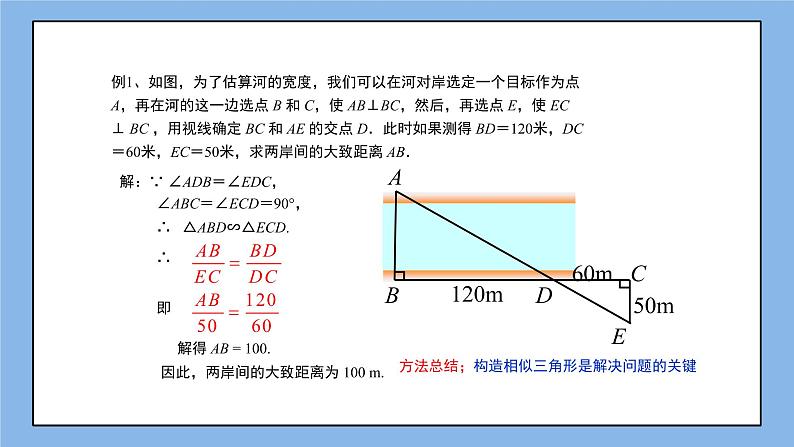
例1、如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点 A,再在河的这一边选点 B 和 C,使 AB⊥BC,然后,再选点 E,使 EC ⊥ BC ,用视线确定 BC 和 AE 的交点 D.此时如果测得 BD=120米,DC=60米,EC=50米,求两岸间的大致距离 AB.
解:∵ ∠ADB=∠EDC,
∠ABC=∠ECD=90°,
∴ △ABD∽△ECD.
解得 AB = 100.
因此,两岸间的大致距离为 100 m.
方法总结;构造相似三角形是解决问题的关键
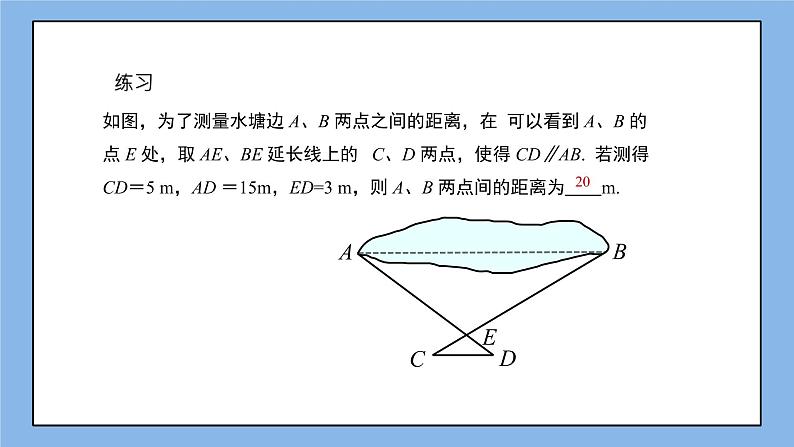
如图,为了测量水塘边 A、B 两点之间的距离,在 可以看到 A、B 的点 E 处,取 AE、BE 延长线上的 C、D 两点,使得 CD∥AB. 若测得 CD=5 m,AD =15m,ED=3 m,则 A、B 两点间的距离为 m.
利用相似三角形测量高度
据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
例2:如图,木杆 EF 长 2 m,它的影长 FD 为3m, 测得 OA 为 201 m,求金字塔的高度 BO.
解:太阳光是平行的光线,因此 ∠BAO =∠EDF.
又 ∠AOB =∠DFE = 90°,∴△ABO ∽△DEF.
因此金字塔的高度为134 m.
1、如图是小明设计用手电来测量某古城墙高度的示意图,点 P 处放一水平的平面镜,光线从点 A出发经平面镜反射后,刚好射到古城墙的顶端 C 处,已知 AB = 2 米,且测得 BP = 3 米,DP = 12 米,那么该古城墙的高度是 ( )
2、如图,九年级某班数学兴趣小组的同学想利用所学 数学知识测量学校旗杆的高度,当身高 1.6 米的楚 阳同学站在 C 处时,他头顶端的影子正好与旗杆顶端的影子重合,同一时刻,其他成员测得 AC = 2 米,AB = 10 米,则旗杆的高度是_____米
例3、如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了?
分析:如图,设观察者眼睛的位置 (视点) 为点 F,画出观察者的水平视线 FG,它交 AB,CD 于点 H,K.视线 FA,FG 的夹角∠AFH 是观察点A 的仰角.类似地,∠CFK 是观察点 C 时的仰角,由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域 (盲区) 之内.再往前走就根本看不到 C 点了.
当∠AFH =∠CFK时 即走到E点使C、A、E三点在同一直线
解:如图,假设观察者从左向右走到点 E 时,她的眼 睛的位置 点 E 与两棵树的顶端点 A,C 恰在一条直线上. 由题意可知,HK=BD=5,HB=KD=1.6,AB=10,CD=12 ∵AB⊥l,CD⊥l,∴AB∥CD. ∴△AEH∽△CEK.
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
方法总结:本题把实际问题抽象到相似三角形中, 利用相似三角形性质列出比例式求解即可.
例4、某同学想利用树影测量树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树影长时,因大树靠近教学楼,有一部分影子在墙上.经测量地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高多少米?
解析: 如图,BC=6.4m,CD=1.4m,MN=1.5m,NP=1.2m
大树的影长不等于地面上部分的加上墙上的
所以要构造三角形满足树高与影长关系,符合相似三角形的条件,即:过D作DE⊥AB于E,则∆AED∽△MNP,可求出AE,再由 AB=AE+BE求树高
解:过D作DE⊥AB于E,则BE=CD==1.4 ED=BC=6.4,∆AED∽△MNP
∴AB=AE+BE=8+1.4=9.4米.
【类型一】利用影长测量高度(长度)
【类型二】利用标杆测量高度(长度)
例5、 如图,某校数学兴趣小组利用自制的直角三角形硬 纸板 DEF 来测量操场旗杆 AB 的高度,他们通过调整测量位置,使斜边 DF 与地面保持平行,并使边DE 与旗杆顶点 A 在同一直线上,已知 DE = 0.5 米, EF = 0.25 米,目测点 D 到地面的距离 DG = 1.5 米,到旗杆的水平距离 DC = 20 米,求旗杆的高度.
DE=0.5米,EF=0.25米,DG=1.5米,DC=20米
故 AB = AC + BC = 10 + 1.5 = 11.5 (m).
答:旗杆的高度为 11.5 m
利用相似解决有遮挡物问题
初中数学湘教版九年级上册3.5 相似三角形的应用优质ppt课件: 这是一份初中数学湘教版九年级上册3.5 相似三角形的应用优质ppt课件,文件包含35相似三角形的应用-课件pptx、35相似三角形的应用-试卷docx、35相似三角形的应用-教学设计docx等3份课件配套教学资源,其中PPT共26页, 欢迎下载使用。
湘教版九年级上册3.5 相似三角形的应用一等奖ppt课件: 这是一份湘教版九年级上册3.5 相似三角形的应用一等奖ppt课件,共15页。PPT课件主要包含了回顾导入,探究新知,DE50m,∵DE50m,课堂练习,解∵AB∥CD,∴CD3m,得x48,课堂小结等内容,欢迎下载使用。
初中数学湘教版九年级上册3.5 相似三角形的应用完美版教学ppt课件: 这是一份初中数学湘教版九年级上册3.5 相似三角形的应用完美版教学ppt课件,文件包含教学课件九上·湘教·35相似三角形的应用pptx、数学九上·湘教·35相似三角形的应用教案docx等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。














