初中数学青岛版七年级下册13.1 三角形备课课件ppt

这是一份初中数学青岛版七年级下册13.1 三角形备课课件ppt，共18页。PPT课件主要包含了学习目标，新课引入，认识三角形的外角，知识讲解，外角个数的探究，典例导学，总结归纳，三角形外角的性质，随堂训练等内容，欢迎下载使用。

1.理解三角形外角的概念, 能识别图形中的外角.2.掌握三角形外角的性质, 熟练运用性质解决问题.
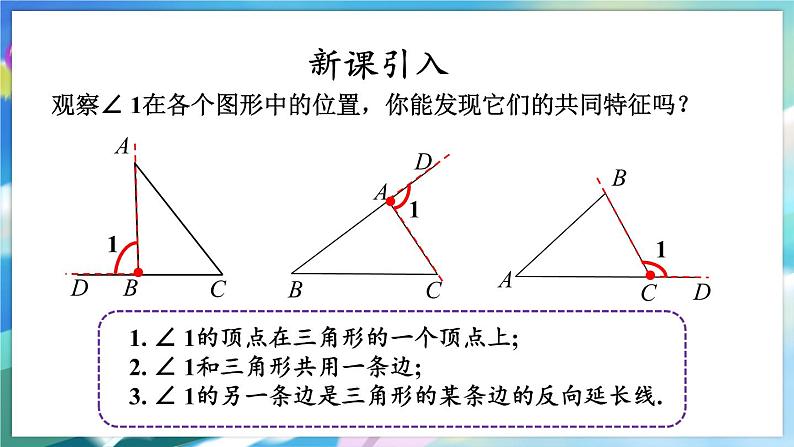
观察∠ 1在各个图形中的位置，你能发现它们的共同特征吗？
1. ∠ 1的顶点在三角形的一个顶点上;2. ∠ 1和三角形共用一条边;3. ∠ 1的另一条边是三角形的某条边的反向延长线.
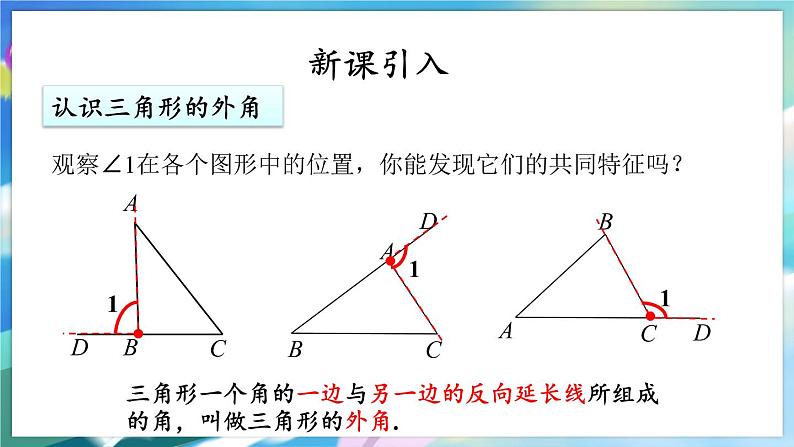
观察∠1在各个图形中的位置，你能发现它们的共同特征吗？
三角形一个角的一边与另一边的反向延长线所组成的角，叫做三角形的外角.
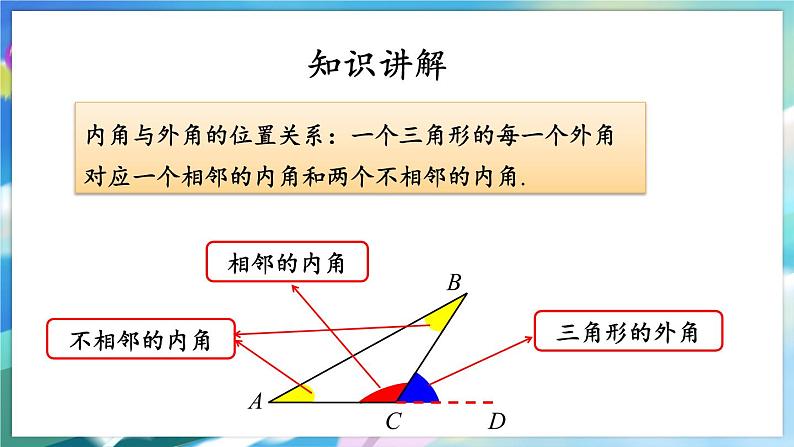
内角与外角的位置关系：一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.
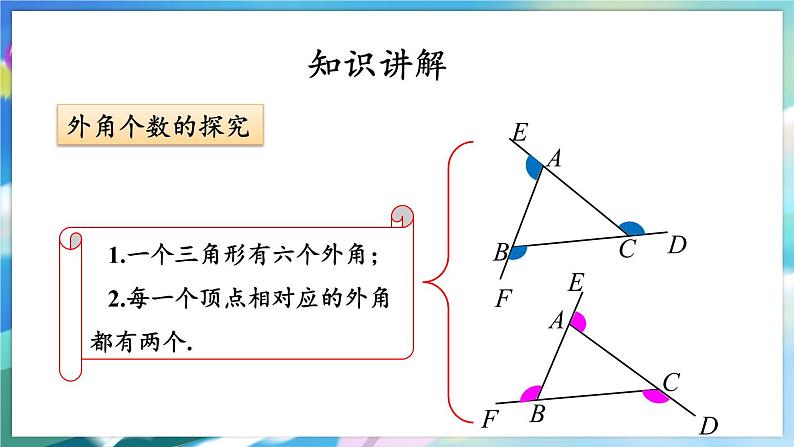
1.一个三角形有六个外角； 2.每一个顶点相对应的外角都有两个.
外角与内角大小关系的探究
若∠BAC=55°，∠B=60°，试求∠ACB, ∠ACD, ∠CAE的度数．
解：根据三角形内角和定理，可以求得∠ACB=180°-55°-60°=65°.因为∠ACB+∠ACD=180°，所以∠ACD=180°-65°=115°=∠BAC+∠B.同理可求得∠CAE=125°=∠B+∠ACB.
∠ACD=∠BAC+∠B.∠CAE=∠B+∠ACB.
三角形的一个外角等于与它不相邻的两个内角的和.
是否适用于所有三角形？
试说明∠ACD=∠B+∠A.
解：过点C作CE平行于AB，
所以∠1=∠B (两直线平行，同位角相等),
∠2=∠A (两直线平行，内错角相等),
所以∠ACD=∠1+ ∠2=∠A+∠B.
不借助辅助线，应该怎么说明？
解：因为∠ACD+∠ACB=180°(邻补角的定义),
又因为∠A+ ∠B+ ∠ACB=180°(三角形内角和定理),
所以， ∠A+ ∠B= ∠ACD (等量代换).
所以∠ACD =180 ° -∠ACB.
所以∠A+ ∠B =180 ° -∠ACB.
若∠ACD=∠B+∠A，
则∠ACD ∠A (<、>)；∠ACD ∠B (<、>).
三角形的一个外角大于任何一个与它不相邻的内角.
例1 如图，∠BCD=92°，∠A=27°，∠BED=44°.求：(1)∠B的度数；(2)∠BFD的度数.
解：(1)在△ABC中，因为∠BCD=∠A+∠B（三角形的一个外角等于与它不相邻的两个内角的和），∠BCD=92°（已知），∠A=27°（已知），所以∠B=∠BCD-∠A=92°-27°=65°.
(2)在△BEF中，因为∠BFD=∠B+∠BEF（三角形的一个外角等于与它不相邻的两个内角的和），∠BED=44°（已知），∠B=65°（已求），所以∠BFD=44°+65°=109°.
例2 如图,在△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连接EF,则∠1,∠2,∠3的大小关系是 .
【解析】比较角的大小关系,首先想到三角形的一个外角大于任何一个与它不相邻的内角.从上面的图形中可以看出：∠1是△ABC的一个外角,所以它大于与它不相邻的内角∠2; 同理,∠2作为△AEF的一个外角,也大于与它不相邻的内角∠3.
三角形的一个外角等于与它不相邻的两个内角之和.
1.如图，已知∠AEC=110°，求∠A+∠B+∠C+∠D的度数.
2.如图,BC⊥ED于O,∠A=27°,∠D=20°, 求∠B和∠ACB 的度数.
分析： ∠B是△ABC的内角,在△ABC中,∠B与∠ACB都是所要求的,而∠ACB又是△COD的外角,根据“三角形的一个外角等于和它不相邻的两个内角的和”可求∠ACB,从而根据三角形的内角和定理可求∠B.