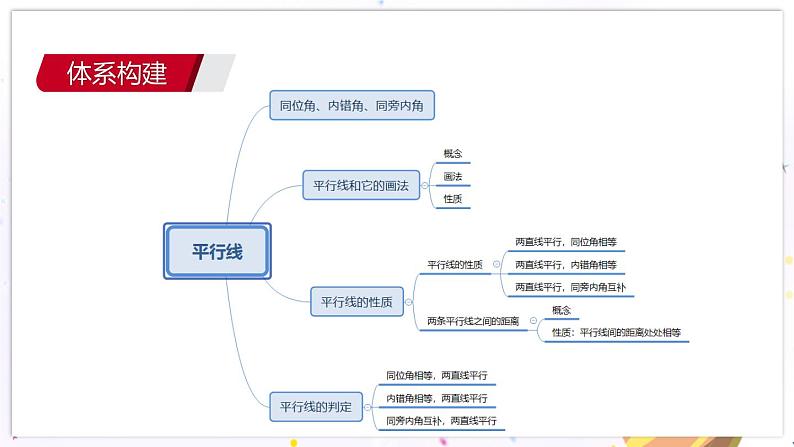
青岛版数学七年级下册 期末复习 专题二 平行线 PPT课件

这是一份青岛版数学七年级下册 期末复习 专题二 平行线 PPT课件，共17页。PPT课件主要包含了归纳总结，变式训练等内容，欢迎下载使用。

考点一　同位角、内错角、同旁内角的识别
【例1】（2019年满城县期末）如图所示，直线AB，CD被直线EF所截，分别交AB，CD于点M，N，NH是一条射线，图中共有多少对同位角？多少对内错角？多少对同旁内角？分别指出这些角.
解：共有6对同位角：∠EMB与∠END、∠EMA与∠ENC、∠AMN与∠CNF、∠BMF与∠DNF、∠EMB与∠ENH、∠BMN与∠HNF；
共有3对内错角：∠BMF与∠MNC、∠AMN与∠MND、∠AMN与∠MNH；共有3对同旁内角：∠AMN与∠MNC、∠BMN与∠MND、∠BMN与∠MNH.
首先弄明白所判断的是哪两个角，其次判断是由哪两条直线被哪条直线所截形成的.其方法是：两个角的公共边所在的直线是截线，其余两边所在的直线是被截的两条直线.
如何正确判断同位角、内错角、同旁内角？
(2019年柳州模拟)如图，与∠1是同旁内角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
考点二　平行线的性质与判定的综合应用
【例2】如图，CD⊥AB于点D，点F是BC上任意一点，FE⊥AB于点E，∠1=∠2，∠3=72°，求∠BCA的度数.
解:因为CD⊥AB，FE⊥AB，所以∠BDC=∠BEF=90°.所以FE//CD，即∠2=∠BCD.因为∠1=∠2，所以∠1=∠BCD.所以DG//BC，即∠BCA=∠3=72°.
(1)平行线的判定是用角的数量关系推出两直线的位置关系；(2)平行线的性质是用两直线的位置关系得到角的数量关系.性质和判定恰好是互为“因果”关系，因此，“欲证平行用判定，已知平行用性质”.
平行线的性质与判定中角的数量关系与直线的位置关系有怎样的因果关系？
1.(2019年山东济宁中考)如图，直线a，b被直线c，d所截，若∠1=∠2，∠3=125°，则∠4的度数是( )
A.65° B.60° C.55° D.75°
解析：如图，因为∠1=∠2，所以a//b，所以∠4=∠5.因为∠5=180°－∠3=55°,所以∠4=55°.
2.如图，∠EBC+∠EFA=180°，∠A=∠C.试说明:AB//CE.
解:因为∠EBC+∠EFA=180°，∠DFB=∠EFA，所以∠EBC+∠DFB=180°，即BC//AD.所以∠EDA=∠C.因为∠A=∠C，所以∠EDA=∠A，所以AB//CE.
考点三 辅助线在平行线中的应用
【例3】如图，AB//EF，∠BCD=90°，试求图中∠α+∠β－∠γ的度数.
解:如图，过点C作CM//AB，过点D作DN//AB.
因为AB//EF，所以AB//CM//DN//EF.
所以∠BCM=∠α，∠DCM=∠CDN，∠EDN=∠γ,因为∠β=∠CDN+∠EDN=∠CDN+∠γ①， ∠BCD=∠α+∠CDN=90°②,由①②得∠a+∠β－∠γ=90°.
条件不足时，如何求角或线段之间的关系？
解决这类问题，一般是先过“拐点”作平行线，将个一角分成两个角或与其他已知角建立联系，再运用平行线的性质，使问题得到解决.
解：AB//CD.理由如下：如图，过点E作EF//AB，则∠ABE+∠BEF=180°.
因为∠ABE+∠BED+∠EDC=360°.所以∠FED+∠EDC=180°,所以EF//CD，即AB//CD.
【变式训练】如图，已知∠B+∠D+∠E=360°，则AB与CD平行吗？为什么？