青岛版数学八年级下册 10.2 第2课时 一次函数的图象 PPT课件

这是一份青岛版数学八年级下册 10.2 第2课时 一次函数的图象 PPT课件，共18页。
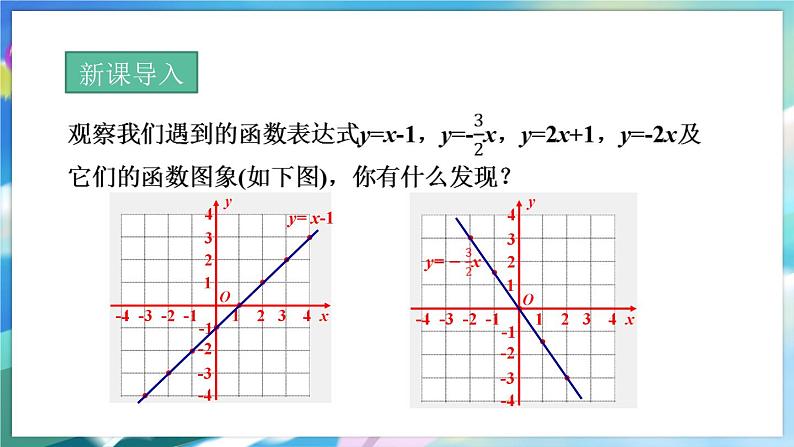
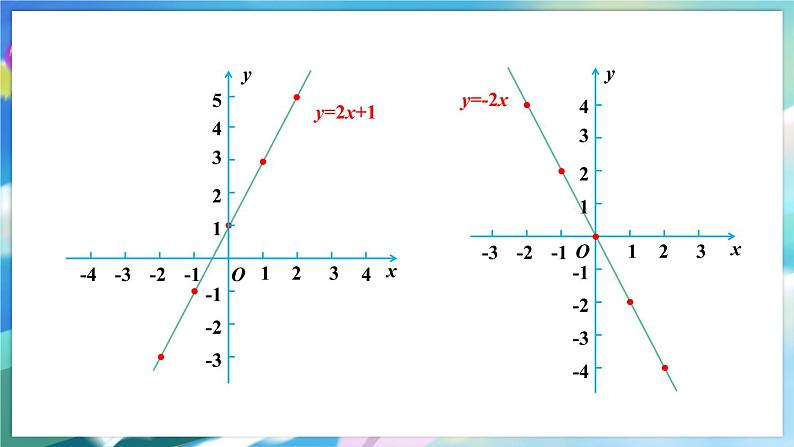
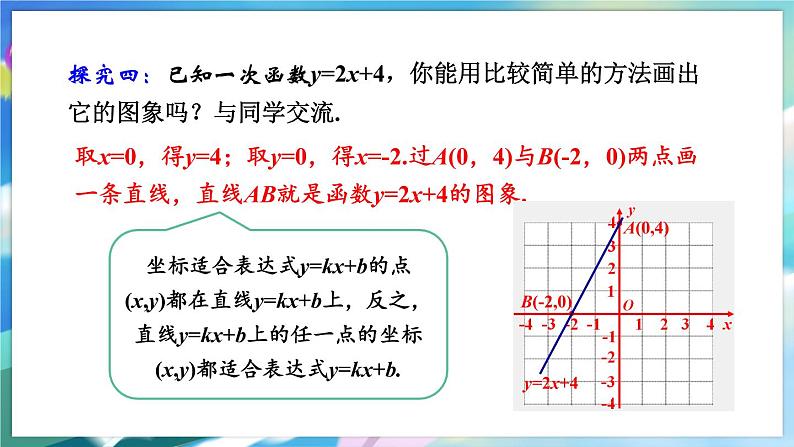
第10章 一次函数10.2 一次函数和它的图象第2课时 一次函数的图象能利用两点法作出一次函数和正比例函数的图象，知道一次函数的图象是一条直线、正比例函数的图象经过原点；理解待定系数法的定义，能用待定系数法求一次函数的表达式.学习目标新课导入 y= x-1 y=-2xy=2x+1新知探究 这些函数都是一次函数.它们的图象都是直线.特别地，正比例函数y=kx的图象都经过原点.一般地，一次函数y=kx+b的图象是一条直线，所以也称为直线y=kx+b.探究二：你能求出一次函数y=kx+b的图象与x轴交点的横坐标吗？你能求出它的图象与y轴交点的纵坐标吗？你能分别说明这两个交点坐标的意义吗？ 探究三：由探究二你发现一次函数y=kx+b的图象与x轴交点的横坐标和一元一次方程kx+b=0的解有什么关系？ 探究四：已知一次函数y=2x+4，你能用比较简单的方法画出它的图象吗？与同学交流.提示：两点确定一条直线.探究四：已知一次函数y=2x+4，你能用比较简单的方法画出它的图象吗？与同学交流.取x=0，得y=4；取y=0，得x=-2.过A(0，4)与B(-2，0)两点画一条直线，直线AB就是函数y=2x+4的图象.y=2x+4坐标适合表达式y=kx+b的点(x,y)都在直线y=kx+b上，反之，直线y=kx+b上的任一点的坐标(x,y)都适合表达式y=kx+b.A(0,4)B(-2,0)探究五：一般地，你认为选取怎样的点画直线y=kx+b（k≠0）比较简便？作直线y=kx（k≠0）呢？ 画直线y=kx(k≠0)时，只要再求出直线上一个不是原点的点，画经过这点和原点的直线就可以了.【例1】已知一次函数的图象如图所示，写出这个函数的表达式.解：设所求函数的表达式为y=kx+b.由图可知，该函数的图象与x轴、y轴的交点坐标分别为(0，-2)，(3，0)，将它们分别代入y=kx+b，得解此二元一次方程组，得 像例1这样，通过先设出表达式中的未知系数，再根据所给条件，利用解方程或方程组确定这些未知系数.这种方法叫做待定系数法.今后在确定函数表达式时，经常用到这种方法.【例2】已知点A(1，0)，B(0，-2).如果直线AB上有一点C在第一象限，且ΔBOC的面积等于2，求点C的坐标.解：设直线AB的函数表达式为y=kx+b(k≠0). 将点A(1，0)，B(0，-2)的坐标分别代入y=kx+b，得解得再将k=2,b=-2代入y=kx+b,得直线AB的函数表达式为y=2x-2 . 设C(x,y)(x＞0,y＞0)，则 你能总结出用待定系数法求一次函数表达式的一般步骤吗？(1)设：设含有待定系数的函数表达式： ； (2)代：把已知条件(自变量与对应的函数值) 代入函数的表达式，得到关于 的方程组；(3)解：解方程组，得k,b的值；(4)写：把求出的k,b的值代回所设的函数的表达式，写出所求的函数表达式.求一次函数表达式的步骤： y=kx+b(k≠0)或y=kxk，b课堂练习1.求下图中直线的函数表达式.解：设所求函数表达式为y=kx+b （k≠0）.因为直线经过点（2，0）, （0，2）， 所以所求函数表达式为y=-x+2.2.(1)在同一直角坐标系中，画出下列三个函数的图象：①y=-x； ② y=-x-2； ③ y=-x+2.解：① y=-x过点(0,0),(1,-1),② y=-x-2过点(0,-2),(-2,0),③ y=-x+2过点(0,2),(2,0),据此，可分别画出它们的函数图象如图.y=-xy=-x-2y=-x+2(2)观察(1)中的三个函数的图象，它们之间有什么关系？你能得出什么结论？解：三条直线互相平行.结论：一般地，两个一次函数y1=k1x+b1(k1≠0)， y2=k2x+b2 (k2≠0)，当k1=k2，b1≠b2时，它们的图象互相平行.课堂小结一般地，一次函数y=kx+b的图象是一条直线，所以也称为直线y=kx+b.1.一次函数的图象2.待定系数法通过先设出表达式中的未知系数，再根据所给条件，利用解方程或方程组确定这些未知系数.这种方法叫做待定系数法.