初中数学青岛版八年级下册第6章 平行四边形6.3 特殊的平行四边形教案配套课件ppt

这是一份初中数学青岛版八年级下册第6章 平行四边形6.3 特殊的平行四边形教案配套课件ppt，共19页。PPT课件主要包含了教学目标，温故知新，探究新知，情境一，符号语言，情境二，课堂练习等内容，欢迎下载使用。

1. 经历探索、猜想、证明的过程，理解并掌握矩形的判定定理；
2. 能做到证明矩形的判定定理以及相关结论，解决相关的实际问题.
1、判断下列命题是否是真命题？ （1）平行四边形的两条对角线的长度相等 （2）矩形相邻的两个角的度数相等 （3）矩形的两条对角线互相平分 （4）矩形的对角线平分它的一组对角
2. 在四边形ABCD中，AC、BD交于点O，在下列各组条件中，不能判定四边形ABCD为矩形的是（　　）A．AB=CD，AD=BC，AC=BDB．AO=CO，BO=DO，∠A=90°C．∠A=∠C，∠B+∠C=180°，AC⊥BDD．∠A=∠B=90°，AC=BD
3．在四边形ABCD中，AC与BD相交于点O，且OA=OC，OB=OD．如果再增加条件AC=BD，此四边形一定是（　　）A．正方形B．矩形C．菱形 D．都有可能
（ ）
矩形定义：有一个角是直角的平行四边形叫做矩形.
（ ）
依据矩形的定义：有一个角是直角的平行四边形是矩形.
你还有其他的判定方法吗？
∵平行四边形ABCD，∠A=90°，∴四边形ABCD是矩形
你知道如何判定一个平行四边形是矩形吗？
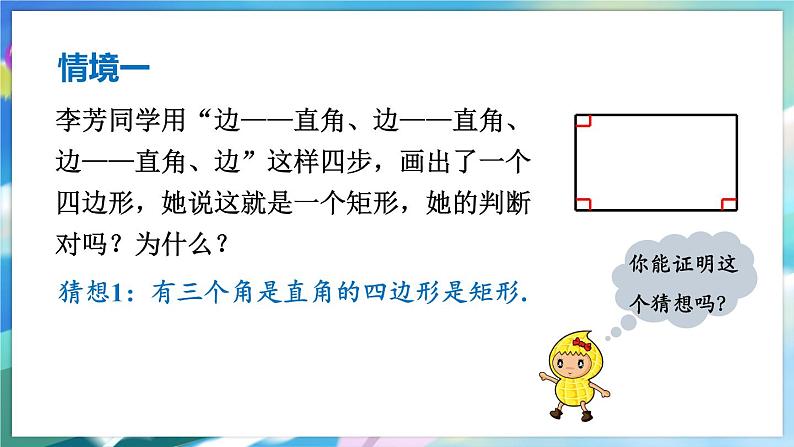
李芳同学用“边——直角、边——直角、边——直角、边”这样四步，画出了一个四边形，她说这就是一个矩形，她的判断对吗？为什么？
猜想1：有三个角是直角的四边形是矩形.
已知：四边形ABCD中，∠A＝∠B＝∠C＝90°.求证：四边形ABCD是矩形.
证明：∵∠A＝∠B＝90°，　
∴∠A＋∠B＝180°　
∴四边形ABCD是平行四边形.　
∴四边形ABCD是矩形.
矩形的判定定理1：有三个角是直角的四边形是矩形.
∵ ∠A=∠B=∠C=90°， ∴四边形ABCD是矩形.
工人师傅为了检验两组对边相等的四边形窗框是否成矩形，一种方法是量一量这个四边形的两条对角线长度，如果对角线长相等，则窗框一定是矩形，你知道为什么吗？
猜想2：对角线相等的平行四边形是矩形.
已知：如图，在平行四边形ABCD中，AC=BD.求证：平行四边形ABCD是矩形.
∵四边形ABCD是平行四边形，∴AB=CD.∵AC=BD，BC=CB，∴△ABC≌△DCB.∴∠ABC=∠DCB.∵AB∥CD，∴∠ABC+∠DCB=180°.∴∠ABC=90°.∴平行四边形ABCD是矩形.　
矩形的判定定理2：对角线相等的平行四边形是矩形.
∵ 四边形ABCD是平行四边形，AC=BD （或OA=OC=OB=OD），∴四边形ABCD是矩形.
【例】下列各句判定矩形的说法是否正确.（1）有一个角是直角的四边形是矩形； （2）有四个角是直角的四边形是矩形； （3）四个角都相等的四边形是矩形； （4）对角线相等的四边形是矩形； （5）对角线相等且互相垂直的四边形是矩形；（6）对角线互相平分且相等的四边形是矩形； （7）对角线相等，且有一个角是直角的四边形是矩形.
1. 已知：如图，在 ABCD中，AC，BD相交于点O，△AOB是等边三角形，求∠ACB的度数.
解：∵△AOB是等边三角形，∴OA=OB. ∵四边形ABCD是平行四边形， ∴OA=OC，OB=OD.∴AC=BD. ∴平行四边形ABCD是矩形. 在Rt△ABC中，∵∠BAC=60°，∴∠ACB=30°.
解：∵四边形ABCD是平行四边形， ∴OA=OC，OB=OD. ∵OA=OD，∴AC=BD. ∴四边形ABCD是矩形. ∴∠DAB=90°. ∵∠OAD=50°，∴∠OAB=40°.
3. 如图，平行四边形ABCD四个内角的平分线围成四边形EFGH，猜想四边形EFGH的形状，并说明理由.
∵四边形ABCD是平行四边形，∴∠DAB+∠ABC=180°.∵AE、BE分别平分∠DAB、∠ABC ， ∴∠EAB+∠EBA=90 °.∴∠AEB=90°，∴∠HEF=90°.同理，∠EFG=90°，∠FGH=90°.∴四边形EFGH是矩形.
解：四边形EFGH是矩形.
4．如图所示，在□ABCD中，E为AD的中点，△CBE是等边三角形，求证：□ABCD是矩形。
5．如图，□ABCD与□ABEF中，BC=BE，∠ABC=∠ABE，求证：四边形EFDC是矩形。