通用版2023届高考数学二轮复习数据分析能力作业含答案

这是一份通用版2023届高考数学二轮复习数据分析能力作业含答案，共40页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
数据分析能力

一、单选题
1. 某高校12名毕业生的起始月薪如下表所示：
毕业生
起始月薪
毕业生
起始月薪
1
2
3
4
5
6
2850
2950
3050
2880
2755
2710
7
8
9
10
11
12
2890
3130
2940
3325
2920
2880
则第85百分位数是．(    )

A. 3050 B. 2950 C. 3130 D. 3325
二、多选题
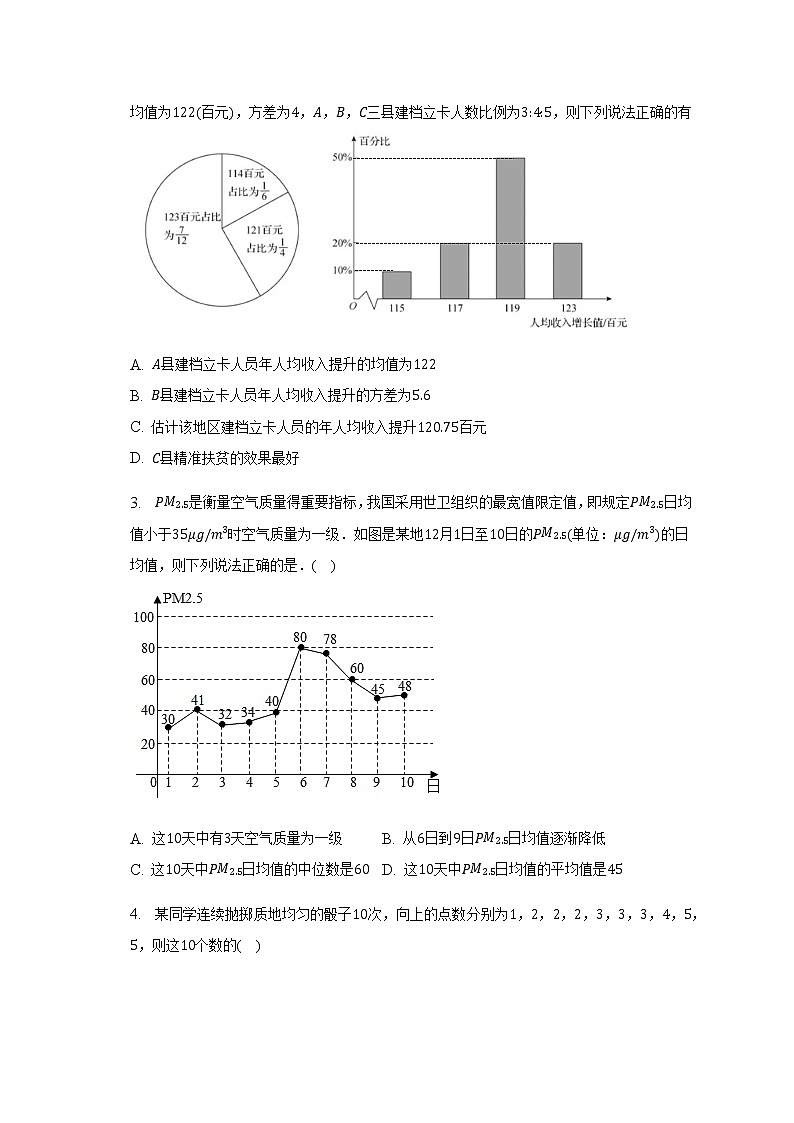
2. 为了解某贫困地区实施精准扶贫后的成果，现随机抽取了该地区三个县市在2021年建档立卡人员年人均收入提升状况.经统计，A县建档立卡人员年人均收入提升状况用饼状图表示，B县建档立卡人员年人均收入提升状况用条形图表示，C县建档立卡人员年人均收入提升的均值为122(百元)，方差为4，A，B，C三县建档立卡人数比例为3:4:5，则下列说法正确的有
A. A县建档立卡人员年人均收入提升的均值为122
B. B县建档立卡人员年人均收入提升的方差为5.6
C. 估计该地区建档立卡人员的年人均收入提升120.75百元
D. C县精准扶贫的效果最好
3. PM2.5是衡量空气质量得重要指标，我国采用世卫组织的最宽值限定值，即规定PM2.5日均值小于35μg/m3时空气质量为一级．如图是某地12月1日至10日的PM2.5(单位：μg/m3)的日均值，则下列说法正确的是．(    )

A. 这10天中有3天空气质量为一级 B. 从6日到9日PM2.5日均值逐渐降低
C. 这10天中PM2.5日均值的中位数是60 D. 这10天中PM2.5日均值的平均值是45
4. 某同学连续抛掷质地均匀的骰子10次，向上的点数分别为1，2，2，2，3，3，3，4，5，5，则这10个数的(    )
A. 众数为2和3 B. 平均数为3
C. 标准差为85 D. 第85百分位数为4.5
5. 给出以下24个数据：
148.0 149.0 154.0 154.0 155.0  155.0  155.2 157.0
158.0  158.0  159.0 159.5  161.5  162.0  162.5  162.5
163.0  163.0 164.0 164.1 165.0 170.0  171.0  172.0
对于以上给出的数据，下列选项正确的为

A. 极差为24.0 B. 第75百分位数为164.0
C. 第25百分位数为155.2 D. 80%分位数为164.1
6. 成立时间少于10年，估值超过10亿美元且未上市的企业，称为独角兽企业．2021年中国新经济独角兽企业分布较广泛，覆盖居民生活的各个方面．如图为2021年中国新经济独角兽企业TOP200的行业分布图，中国新经济独角兽企业TOP200榜单中，京、沪、粤三地的企业数量共同占比达到69%.下列说法正确的是(    )
A. 随着智能出行与共享经济观念的普及，汽车交通行业备受投资者关注
B. 这12个行业TOP200榜单中独角兽企业数量的中位数是17
C. 中国新经济独角兽企业TOP200榜单中，京、沪、粤三地的企业超过130家
D. 2021年中国新经济独角兽企业TOP200榜单中汽车交通、企业服务、文化娱乐的企业数量共同占比超过40%
7. 下图为2022年8月5日通报的14天内31省区市疫情趋势，则下列说法正确的是(    )
A. 无症状感染者的极差大于400 B. 确诊病例的方差大于无症状感染者的方差
C. 实际新增感染者的平均数小于389 D. 实际新增感染者的第80百分位数为641
8. 睡眠很重要，教育部《关于进一步加强中小学生睡眠管理工作的通知》中强调“小学生每天睡眠时间应达到10小时，初中生应达到9小时，高中生应达到8小时”.某机构调查了1万个学生时间利用信息得出如图，则以下判断正确的有(    )

A. 高三年级学生平均学习时间最长
B. 中小学生的平均睡眠时间都没有达到《通知》中的标准，其中高中生平均睡眠时间最接近标准
C. 大多数年龄段学生平均睡眠时间长于学习时间
D. 与高中生相比，大学生平均学习时间大幅下降，释放出的时间基本是在睡眠
9. 2021年4月至2021年12月我国规模以上工业天然气产量保持平稳，日均产量(亿立方米)与当月增速(%)如图所示，则(    )

备注：日均产品产量是以当月公布的我国规模以上工业企业总产量除以该月日历天数计算得到．
当月增速=当月产量-去年同期产量去年同期产量×100％．

A. 2021年12月份我国规模以上工业天然气产量当月增速比上月放缓2.1个百分点
B. 2021年4月至2021年12月我国规模以上工业天然气产量当月增速的极差为12.6%
C. 2021年7月份我国规模以上工业天然气产量为153亿立方米
D. 2021年4月至2021年12月我国规模以上工业天然气日均产量的40%分位数为5.3亿立方米
10. 某校高一(1)班王伟、张诚、赵磊三名同学六次数学测试的成绩及班级平均分如表，根据成绩表作出如图，则下列说法正确的是(    )

第一次
第二次
第三次
第四次
第五次
第六次
王伟
98
87
91
92
88
95
张诚
90
76
88
75
86
80
赵磊
68
65
73
72
75
82
班级平均分
88.2
78.3
85.4
80.3
75.7
82.6

A. 王伟同学的数学学习成绩始终高于班级平均水平
B. 张诚同学的数学学习成绩始终高于班级平均水平
C. 赵磊同学的数学学习成绩低于班级平均水平，但与班平均分的差距逐步缩小
D. 赵磊同学的数学成绩波动上升
11. 某市为了解全市居民月用水量，随机抽取了1000户居民进行调查，发现他们的月用水量都在0∼24t之间，进行等距离分组，如下图1是分成6组、图2是分成12组后分别画出的频率分布直方图：
则下列说法正确的是(    )

A. 由图1知，抽取的月用水量在[4,8)的居民有50户
B. 由图1知，月用水量的90%分位数为18t
C. 由图1估计全市居民月用水量的平均值为7.76t
D. 图1中：组数少，组距大，容易看出数据整体的分布特点;图2中：组数多，组距小，不容易看出数据整体的分布特点
12. 已知随机变量X的取值为不大于n(n∈N*)的非负整数，它的概率分布列为
X
0
1
2
3
…
n
p
p0
p1
p2
p3
…
pn
其中pi(i=0,1,2,3,⋯,n)满足pi∈[0,1]，且p0+p1+p2+⋯+pn=1.定义由X生成的函数f(x)=p0+p1x+p2x2+p3x3+⋯+pixi+⋯+pnxn，g(x)为函数f(x)的导函数，E(X)为随机变量X的期望．现有一枚质地均匀的正四面体型骰子，四个面分别标有1，2，3，4个点数，这枚骰子连续抛掷两次，向下点数之和为X，此时由X生成的函数为f1(x)，则      (    )

A. E(X)=g(2) B. f1(2)=152 C. E(X)=g(1) D. f1(2)=2254
三、填空题
13. 已知某区甲、乙、丙三所学科基地学校的数学强基小组人数分别为24，8，16人，在一次统一考试中，该区三所学校强基学生的平均分分别为118，120，114，方差分别为15，12，21，则该区所有数学强基学生成绩的平均数x=          ，方差S2=          ．
四、解答题
14. (本小题12.0分)
数字人民币是由央行发行的法定数字货币，它由指定运营机构参与运营并向公众兑换，与纸钞和硬币等价.截至2021年6月30日，数字人民币试点场景已超132万个，覆盖生活缴费、餐饮服务、交通出行、购物消费、政务服务等领域.为了进一步了解普通大众对数字人民币的感知以及接受情况，某机构进行了一次问卷调查，结果如下：

(1)如果将高中及高中以下的学历称为“低学历”，大学专科及以上学历称为“高学历”，根据所给数据，完成2×2列联表．

(2)若从低学历的被调查者中随机抽取2人进行进一步调查，求被选中的2人中至少有1人对数字人民币不了解的概率;
(3)根据2×2列联表，判断是否有95%的把握认为“是否了解数字人民币”与“学历高低”有关?
附：χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)．


15. (本小题12.0分)
随着教育信息化2.0时代的到来，依托网络进行线上培训越来越便捷，逐步成为实现全民终身学习的重要支撑.最近某高校继续教育学院采用线上和线下相结合的方式开展了一次300名学员参加的“国学经典诵读”专题培训.为了解参训学员对于线上培训、线下培训的满意程度，学院随机选取了50名学员，将他们分成两组，每组25人，分别对线上、线下两种培训进行满意度测评，统计学员的评分(满分100分)如下：
线上培训：65 65 66 67 67 68 69 72 73 74 75 75 76 77
                 77 78 78 79 81 81 83 85 86 88 91
线下培训：69 73 76 77 78 79 79 80 82 83 84 85 85 76
                 87 87 88 89 91 92 93 94 94 95 96
(1)求50名学员满意度评分的中位数m，并将评分不超过m、超过m分别视为“基本满意”“非常满意”两个等级.利用样本估计总体的思想，估算本次培训共有多少学员对线上培训非常满意．
(2)根据题中数据填写下面的列联表：

基本满意
非常满意
线上培训


线下培训


并根据列联表判断能否有99.5%的把握认为学员对两种培训方式的满意度有差异?
附：χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)，n=a+ b+c+d．
P(χ2≥k)
0.010
0.005
0.001
k
6.635
7.879
10.828

16. (本小题12.0分)
某地区2023年清明节前后3天每天下雨的概率为70%，通过模拟实验的方法来计算该地区这3天中恰好有2天下雨的概率：用随机数x(x∈N，且0≤x≤9)表示是否下雨：当x∈0,mm∈Z时表示该地区下雨，当x∈m+1,9时，表示该地区不下雨，从随机数表中随机取得20组数如下
332  714  740  945  593  468  491  272  073  445
992  772  951  431  169  332  435  027  898  719
(1)求m的值，并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率；
(2)从2014年开始到2022年该地区清明节当天降雨量(单位：mm)如下表：(其中降雨量为0表示没有下雨)．
时间
2014年
2015年
2016年
2017年
2018年
2019年
2020年
2021年
2022年
年份t
1
2
3
4
5
6
7
8
9
降雨量y
29
28
26
27
25
23
24
22
21
经研究表明：从2014年开始至2022年，该地区清明节有降雨的年份的降雨量y与年份t成线性回归，求回归直线∧ =∧ t+∧ ，并计算如果该地区2023年(t=10)清明节有降雨的话，降雨量为多少？(精确到0.01)
参考公式：b=i=1nti-tyi-yi=1nti-t2；参考数据：i=19ti-tyi-y=-58，i=19ti-t2=60

17. (本小题12.0分)
黄冈市某中学利用周末开展“日常生活劳动、生产劳动，我能行”活动.为了调查高一、高二学生劳动实践活动情况，对这两个年级的各1000名学生分别统计了每周的劳动时间数，如下图表．

高一劳动时间(小时)
[1,2)
[2,3)
[3,4)
[4,5)
[5,6)
人数
40
160
280
400
120
(1)根据提供的数据，直接在答题卡中补充完整高一年级周劳动时间的频率分布直方图(不需要书写具体步骤) ;
(2)通过比较高一、高二年级的周劳动时间平均数，说说哪个年级更热爱劳动?(同一组数据用该组区间的中点值为代表)
(3)根据图表，估计高一年级周劳动时间的样本数据80％分位数．
18. (本小题12.0分)
某公司在2013～2021年生产经营某种产品的相关数据如表所示：
年份
2013
2014
2015
2016
2017
2018
2019
2020
2021
年生产台数(单位：万台)
3
4
5
6
6
9
10
10
a
年返修台数(单位：台)
32
38
54
58
52
71
80
75
b
年利润(单位：百万元)
3.85
4.50
4.20
5.50
6.10
9.65
10.00
11.50
c
注：年返修率=年返修台数年生产台数．
(Ⅰ)从2013～2020年中随机抽取一年，求该年生产的产品的平均利润不小于100元/台的概率；
(Ⅱ)公司规定：若年返修率不超过千分之一，则该公司生产部门当年考核优秀.现从2013～2020年中随机选出3年，记ξ表示这3年中生产部门获得考核优秀的次数.求ξ的分布列和数学期望；
(Ⅲ)记公司在2013～2015年，2016～2018年，2019～2021年的年生产台数的方差分别为s12，s22，s32.若s32≤max{s12,s22}，其中max{s12,s22}表示s12，s22这两个数中最大的数.请写出a的最大值和最小值.(只需写出结论)
(注：s2=1n[(x1-x-)2+(x2-x-)2+⋅⋅⋅(xn-x-)2]，其中x-为数据x1，x2，⋅⋅⋅，xn的平均数)
19. (本小题12.0分)
漳州布袋木偶戏是传统民俗艺术，2006年被列入首批国家非物质文化遗产保护．据《漳州府志》记载，漳州地区在宋代就已经有布袋木偶戏了．清朝中叶后，布袋木偶戏开始进入兴盛时期，一直到抗日战争前，漳州的龙溪、漳浦、海澄、长泰等县，几乎乡乡都有专业或者业余的戏班．现今，随着漳州市木偶剧团和木偶学校的蓬勃发展，漳州布袋木偶戏在传承的基础上，不断创新和发展壮大，走向更广阔的世界．为了了解民众对布袋木偶戏的了解程度，厦门中学生助手微信公众号随机抽取了漳州地区男女各100名市民，进行问卷调查，根据调查结果绘制出得分条形图，如图所示．


不够了解
相对了解
合计
男



女



合计



(1)若被调查者得分低于60分，则认为是不够了解布袋木偶戏，否则认为是相对了解布袋木偶戏．根据条形图，完成2×2联表，并根据列联表，判断能否有90%的把握认为对布袋木偶戏的了解程度与性别有关？
(2)恰逢三八妇女节，该单位对参与调查问卷的女市民制定如下抽奖方案：得分低于60分的可以获得1次抽奖机会，得分不低于60分的可以获得2次抽奖机会，每次抽奖结果相互独立．在一次抽奖中，获得一个木偶纪念品的概率为13，获得两个木偶纪念品的概率为16，不获得木偶纪念品的概率为12，在这100名女市民中任选一人，记X为她获得木偶纪念品的个数，求X的分布列和数学期望．
参考公式：
K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)
参考数据：
P(K2≥k0)
0.100
0.050
0.010
0.001
k0
2.706
3.841
6.635
10.828

20. (本小题12.0分)
受疫情影响，某校实行线上教学，为了监控学生的学习情况，每周进行一次线上测评，连续测评5周，得到均分数据见图．


优秀数
非优秀数
合计
某校
46
54
100
联谊校
56
44
100
合计
102
98
200
(1)请你根据数据利用相关系数判定均分y与线上教学周数x是否具有显著相关关系，若有，求出线性回归方程，若没有，请说明理由；
(2)为了对比研究，该校和其水平相当的线下教学的联谊校进行同步测评，从两校分别随机抽取100名同学成绩进行优秀学生数统计见表1，请问是否有把握断定优秀数与线上学习有关？若有关，请问有多大把握？
附：相关系数：r=i=1nxi-xyi-yi=1nxi-x2i=1nyi-y2
回归系数：b=i=1n xiyi-nxyi=1n xi2-n(x)2=i=1n (xi-x)(yi-y)i=1n (xi-x)2a=y-bx.,χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)
临界值表：
Pχ2≥k
0.100
0.050
0.010
0.001
k
2.706
3.841
6.635
10.828

21. (本小题12.0分)
下表为从某患者动态心电图中获取的二十四小时的心率数据(单位：次分钟)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
最慢心率x
65
70
68
72
70
72
62
61
71
78
72
72
73
60
65
65
65
62
64
62
62
65
72
67
最快心率y
98
102
93
100
91
99
106
123
132
146
146
138
94
89
85
90
91
83
88
87
88
90
105
94
平均心率
73
79
79
79
75
82
80
86
94
100
102
93
82
74
72
74
71
68
69
66
67
71
87
76
(1)求最快心率y与最慢心率x的线性经验回归方程y=bx+a(a,b保留小数点后一位);
(Ⅱ)依据已有数据估计该病患后续的心率变化．
(i)设该病患后续48小时中平均心率大于等于100次/分的小时数为随机变量X，估计X的期望;
(ii)若该病患在后续48小时中共测出10小时平均心率大于等于100次/分，请运用统计学中的3σ原理分析该结果．
参考公式：b=i=1n(xi-x)(yi-y)i=1n(xi-x)2，a=y-bx．
参考数据：x=67.3，y=102.4，x2=4529.3，x⋅y=6891.5，124i=124x1y1=6943.5，124i=124xi2=4550.2

22. (本小题12.0分)
中国是茶的故乡，也是茶文化的发源地．为了弘扬中国茶文化，某酒店推出特色茶饮，按事先拟定的价格进行试销，得到销售数据(xi,yi)(i=1,2,…,6)，如下表所示：
试销单价x(元)
20
25
30
35
40
45
销量y(壶)
m
88
86
76
73
68
参考数据：y=16i=16yi=80.5，i=16xiyi=15260，i=16xi2=6775，6×32.52=6337.5．
(1)已知变量x，y具有线性相关关系，求销量y(壶)关于试销单价x(元)的线性回归方程y=bx+a和m的值；
(2)用yi表示根据线性回归方程得到的与xi对应的销量的估计值，当销售数据(xi,yi)中yi与估计值yi满足|yi-yi|≤1时，则称该销售数据(xi,yi)为一组“理想数据”.现从6组销售数据中任取2组，求抽取的2组销售数据中至少有1组是“理想数据”的概率．
附：回归直线方程y=bx+a的斜率b=i=1nxiyi-nxyi=1nxi2-nx2，截距a=y-bx．

23. (本小题12.0分)
某企业计划新购买100台设备，并将购买的设备分配给100名年龄不同(视为技术水平不同)的技工加工一批模具，因技术水平不同而加工出的产品数量不同，故产生的经济效益也不同.若用变量x表示不同技工的年龄，变量y为相应的效益值(元)，根据以往统计经验，他们的工作效益满足最小二乘法，且y关于x的线性回归方程为y=1.2x+40.6．
(1)试预测一名年龄为52岁的技工使用该设备所产生的经济效益；
(2)试根据r的值判断使用该批设备的技工人员所产生的的效益与技工年龄的相关性强弱(0.75≤r≤1，则认为y与x线性相关性很强；r