2023届高考数学二轮复习专题九瓶颈题突破_第3讲应用问题中的“瓶颈题”作业含答案

这是一份2023届高考数学二轮复习专题九瓶颈题突破_第3讲应用问题中的“瓶颈题”作业含答案，共21页。试卷主要包含了解答题等内容，欢迎下载使用。

一、解答题（共21小题）
1. 某工厂有容量为 300 t 的水塔一个，每天从早上 6 时起到晚上 10 时止供应该厂生活和生产用水．已知该厂生活用水为每小时 10 t，工业用水量 W（单位：t）与时间 t（单位：h，定义早上 6 时 t=0）的函数关系式为 W=100t，水塔的进水量有 10 级，第一级每小时进水 10 t，以后每提高一级，每小时的进水量增加 10 t，若某天水塔原有水 100 t，在供水同时打开进水管．
（1）设进水量选用第 n 级，写出在 t 时刻时水的存有量；
（2）问：进水量选择第几级，既能保证该厂用水（水塔中水不空）又不会使水溢出?
2. 某学校为了支持生物课程基地研究植物生长，计划利用学校空地建造一间室内面积为 900 m2 的矩形温室，在温室内划出三块全等的矩形区域，分别种植三种植物，相邻矩形区域之间间隔 1 m，三块矩形区域的前、后与内墙各保留 1 m 宽的通道，左、右两块矩形区域分别与相邻的左、右内墙保留 3 m 宽的通道，如图，设矩形温室的室内长为 x（单位：m），三块种植植物的矩形区域的总面积为 S（单位：m2）．
（1）求 S 关于 x 的函数关系式；
（2）求 S 的最大值．
3. 从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业，根据规划，本年度投入 800 万元，以后每年投入将比上年减少 15，本年度当地旅游业收入估计为 400 万元，由于该项建设对旅游业的促进作用，预计今后的旅游业收入每年会比上年增加 14．
（1）设 n 年内（本年度为第一年）总投入为 an 万元，旅游业总收入为 bn 万元，试写出它们的表达式；
（2）问：至少经过几年旅游业的总收入才能超过总投入?
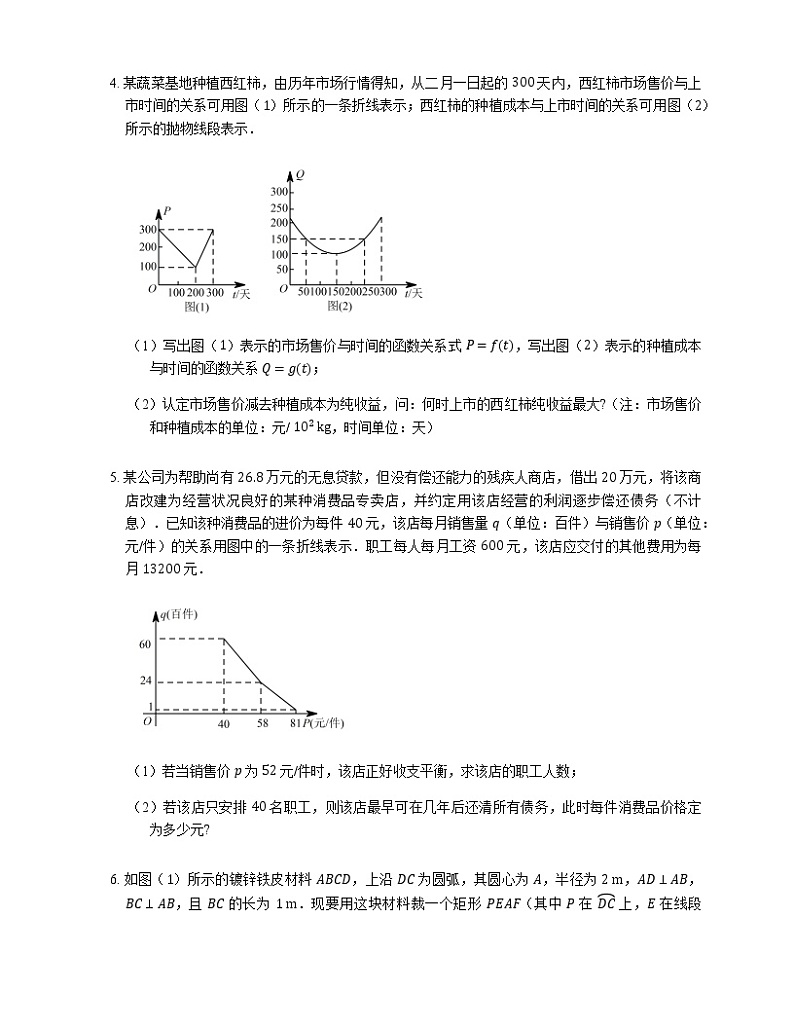
4. 某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的 300 天内，西红柿市场售价与上市时间的关系可用图（1）所示的一条折线表示；西红柿的种植成本与上市时间的关系可用图（2）所示的抛物线段表示．
（1）写出图（1）表示的市场售价与时间的函数关系式 P=ft，写出图（2）表示的种植成本与时间的函数关系 Q=gt；
（2）认定市场售价减去种植成本为纯收益，问：何时上市的西红柿纯收益最大?（注：市场售价和种植成本的单位：元/ 102 kg，时间单位：天）
5. 某公司为帮助尚有 26.8 万元的无息贷款，但没有偿还能力的残疾人商店，借出 20 万元，将该商店改建为经营状况良好的某种消费品专卖店，并约定用该店经营的利润逐步偿还债务（不计息）．已知该种消费品的进价为每件 40 元，该店每月销售量 q（单位：百件）与销售价 p（单位：元/件）的关系用图中的一条折线表示．职工每人每月工资 600 元，该店应交付的其他费用为每月 13200 元．
（1）若当销售价 p 为 52 元/件时，该店正好收支平衡，求该店的职工人数；
（2）若该店只安排 40 名职工，则该店最早可在几年后还清所有债务，此时每件消费品价格定为多少元?
6. 如图（1）所示的镀锌铁皮材料 ABCD，上沿 DC 为圆弧，其圆心为 A，半径为 2 m，AD⊥AB，BC⊥AB，且 BC 的长为 1 m．现要用这块材料裁一个矩形 PEAF（其中 P 在 DC 上，E 在线段 AB 上，F 在线段 AD 上）作圆柱的侧面，若以 PE 为母线，问：如何裁剪可使圆柱的体积最大?其最大值是多少?
7. 某中心接到其正东、正西、正北方向三个观测点的报告：正西、正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其他两观测点晚 4 s．已知各观测点到该中心的距离都是 1020 m．试确定该巨响发生的位置．（假定当时声音传播的速度为 340 m/s，相关各点均在同一平面上）
8. 某山区外围有两条相互垂直的直线型公路，为进一步改善山区的交通现状，计划修建一条连接两条公路的山区边界的直线型公路，记两条相互垂直的公路为 l1，l2，山区边界曲线为 C，计划修建的公路为 l，如图所示，M，N 为 C 的两个端点，测得点 M 到 l1，l2 的距离分别为 5 km 和 40 km，点 N 到 l1，l2 的距离分别为 20 km 和 2.5 km，以 l1，l2 所在的直线分别为 x，y 轴，建立平面直角坐标系 xOy，假设曲线 C 符合函数 y=ax2+b（其中 a，b 为常数）模型．
（1）求 a，b 的值．
（2）设公路 l 与曲线 C 相切于点 P，点 P 的横坐标为 t．
①请写出公路 l 长度的函数解析式 ft，并写出其定义域；
②当 t 为何值时，公路 l 的长度最短?求出最短长度．
9. 某隧道设计为双向四车道，车道总宽 20 m，要求通行车辆限高 4.5 m，隧道口截面的拱线近似地看成抛物线形状的一部分，如图所示建立平面直角坐标系 xOy．
（1）若最大拱高 h 为 6 m，则隧道设计的拱宽 l 是多少．
（2）为了使施工的土方工程量最小，需隧道口截面面积最小. 现隧道口的最大拱高 h 不小于 6 m，则应如何设计拱高 h 和拱宽 l，使得隧道口截面面积最小．（隧道口截面面积公式为 S=23lh）
10. 如图所示，为保护河上古桥 OA ，规划建一座新桥 BC，同时设立一个圆形保护区．规划要求：新桥 BC 与河岸 AB 垂直；保护区的边界是以圆心 M 在线段 OA 上并与 BC 相切的圆，且古桥两端点 O 和 A 到该圆上任意一点的距离均不少于 80 m .经测量，点 A 位于点 O 正北方向 60 m 处，点 C 位于点 O 正东方向 170 m 处（OC 为河岸），tan∠BCO=43 .
（1）求新桥 BC 的长；
（2）当 OM 多长时，圆形保护区的面积最大?
11. 某企业拟建造如图所示的容器（不计厚度，长度单位：m），其中容器的中间为圆柱形，高为 l，左、右两端均为半球形，半径为 r，按照设计要求容器的体积为 80π3 m3，且 l≥2r．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为 3 千元，半球形部分每平方米建造费用为 cc>3 千元．设该容器的建造费用为 y 千元．
（1）求 y 关于 r 的函数解析式，并求该函数的定义域；
（2）求该容器的建造费用最小时半径 r 的值．
12. 现需要设计一个仓库，它由上下两部分组成，如图，上部分的形状是正四棱锥 P-A1B1C1D1，下部分的形状是正四棱柱 ABCD-A1B1C1D1，并要求正四棱柱的高 O1O 是正四棱锥的高 PO1 的四倍．
（1）若 AB=6 m，PO1=2 m，则仓库的容积是多少?
（2）若正四棱锥的侧棱长为 6 m，则当 PO1 为多少时，仓库的容积最大?
13. 如图，某园林单位准备绿化一块直径为 BC 的半圆形空地，△ABC 外的地方种草，△ABC 的内接正方形 PQRS 为一水池，其余的地方种花，若 BC=a，∠ABC=θ，设 △ABC 的面积为 S1，正方形 PQRS 的面积为 S2．
（1）用 a，θ 表示 S1 和 S2；
（2）当 a 固定，θ 变化时，求 S1S2 的最小值．
14. 如图，游客从某旅游景区的景点 A 处下山至 C 处有两种路径．一种是从 A 处沿直线步行到 C 处，另一种是先从 A 处沿索道乘缆车到 B 处，然后从 B 处沿直线步行到 C 处．现有甲、乙两位游客从 A 处下山，甲沿 AC 匀速步行，速度为 50 m/min．在甲出发 2 min 后，乙从 A 处乘缆车到 B 处，在 B 处停留 1 min 后，再从 B 处匀速步行到 C 处．假设缆车匀速直线运动的速度为 130 m/min，山路 AC 长为 1260 m，经测量，csA=1213，csC=35．
（1）求索道 AB 的长；
（2）问：乙出发多少分钟后，乙在缆车上与甲的距离最短?
（3）为使两位游客在 C 处相互等待的时间不超过 3 min，乙步行的速度应控制在什么范围内?
15. 如图，某森林公园有一直角梯形区域 ABCD，其四条边均为道路，AD∥BC，∠ADC=90∘，AB=5 km，BC=8 km，CD=3 km．现甲、乙两管理员同时从 A 地出发匀速前往 D 地，甲的路线是 AD，速度为 6 km/h，乙的路线是 ABCD，速度为 v km/h．
（1）若甲、乙两管理员到达 D 地的时间相差不超过 15 min，求乙的速度 v 的取值范围；
（2）已知对讲机有效通话的最大距离是 5 km，若乙先到达 D 地，且乙从 A 到 D 的过程中始终能用对讲机与甲保持有效通话，求乙的速度 v 的取值范围．
16. 某工厂有工人 214 名，现要生产 1500 件产品，每件产品由 3 个A型零件和 1 个B型零件配套组成，每个工人加工 5 个A 型零件与加工 3 个B型零件所需的时间相同，现将工人分成两组，分别加工一种零件，同时开始加工．设加工A 型零件的工人有 x 人，在单位时间里每一个工人加工A 型零件 5k 件，加工完A型零件所需时间为 gx，加工完B型零件所需时间为 hx．
（1）比较 gx 与 hx 的大小，并写出完成总任务的时间 fx 的解析式；
（2）应怎样分组，才能使完成任务用时最少?
17. 商学院为推进后勤社会化改革，与桃园新区商定：由该区向建设银行贷款 500 万元在桃园新区为学院建一栋可容纳一千人的学生公寓，工程于 2012 年初动工，年底竣工并交付使用，公寓管理处采用收费还贷偿还建行贷款（年利率 5%，按复利计算），公寓所收费用除去物业管理费和水电费 18 万元．其余部分全部在年底还建行贷款．（参考数据：lg1.7343≈0.2391，lg1.05≈0.0212，1.058≈1.4774）
（1）若公寓收费标准定为每生每年 800 元，问到哪一年可偿还建行全部贷款；
（2）若公寓管理处要在 2020 年底把贷款全部还清，则每生每年的最低收费标准是多少元（精确到元）．
18. 某地今年年初有居民住房面积为 a m2，其中需要拆除的旧房面积占了一半，当地有关部门决定每年以当年年初住房面积的 10% 的住房增长率建设新住房，同时每年拆除 x m2 的旧住房，又知该地区人口年增长率为 4.9‰．
注：下列数据供计算时参考：
1.19=
（1）如果 10 年后该地区的人均住房面积正好比目前翻一番，那么每年应拆除的旧住房面积 x 是多少?
（2）依照（1）的拆房速度，共需多少年能拆除所有需要拆除的旧房?
19. 某网络营销部门随机抽查了某市 200 名网友在 2016 年 11 月 11 日的网购金额，所得数据如图（1）：已知网购金额不超过 3 千元与超过 3 千元的人数比恰好为 3:2．
网购金额单位:千元频数频率0,1160.081,2240.122,3xp3,4yq4,5160.085,6140.07合计2001.00
图（1）
（1）试确定 x，y，p，q 的值，并补全频率分布直方图（2）；
（2）营销部门为了了解该市网友的购物体验，在这 200 名网友中，用分层抽样的方法从网购金额在 1,2 和 4,5 的两个群体中抽取 5 人进行问卷调查，若需从这 5 人中随机选取 2 人继续访谈，则此 2 人来自不同群体的概率是多少?
20. 某宾馆在装修时，为了美观，欲将客房的窗户设计成半径为 1 m 的圆形，并用四根木条将圆分成如图所示的 9 个区域，其中四边形 ABCD 为中心在圆心的矩形．现计划将矩形 ABCD 区域设计为可推拉的窗口．
（1）若窗口 ABCD 为正方形，且面积大于 14 m2（木条宽度忽略不计），求四根木条总长的取值范围；
（2）若四根木条总长为 6 m，求窗口 ABCD 面积的最大值．
21. 如图，阴影部分为古建筑物保护群所在地，其形状是以 O1 为圆心、半径为 1 km 的半圆面．公路 l 经过点 O，且与直径 OA 垂直．现计划修建一条与半圆相切的公路 PQ（点 P 在直径 OA 的延长线上，点 Q 在公路 l 上），T 为切点．
（1）按下列要求建立函数关系：
①设 ∠OPQ=α（单位：rad），将 △OPQ 的面积 S 表示为 α 的函数；
②设 OQ=t（单位：km），将 △OPQ 的面积 S 表示为 t 的函数．
（2）请你选用（1）中的一个函数关系，求 △OPQ 的面积 S 的最小值．
答案
1. （1） 略．
（2） 略．
2. （1） S=-2x-7200x+916，x∈8,450．
（2） 676 m2．
3. （1） 第 1 年投入 800 万元，
第 2 年投入 800×1-15 万元，
⋯，
第 n 年投入 800×1-15n-1 万元，
所以 n 年内的总投入
an=800+800×1-15+⋯+800×1-15n-1=4000×1-45n;
第 1 年旅游业收入为 400 万元，
第 2 年旅游业收入为 400×1+14 万元，
⋯，
第 n 年旅游业收入为 400×1+14n-1 万元，
所以 n 年内的总收入
bn=400+400×1+14+⋯+400×1+14n-1=1600×54n-1.
（2） 设至少经过 n 年旅游业的总收入才能超过总投入，
所以 bn-an>0，即 1600×54n-1-4000×1-45n>0，
化简，得 5×45n+2×54n-7>0，即 45n<25，可得 n≥5，
所以至少要经过 5 年旅游业的总收入才能超过总投入．
4. （1） 由图（1）可得市场售价与时间的函数关系为 ft=300-t,0≤t≤2002t-300,200由图（2）可得种植成本与时间的函数关系为 gt=t-1502200+100，0≤t≤300．
（2） 设 t 时刻的纯收益为 ht，则由题意得 ht=ft-gt，
即 ht=-1200t2+12t+1752,0≤t≤200-1200t2+72t-10252,200当 0≤t≤200 时，配方整理得 ht=-1200t-502+100，
所以当 t=50 时，ht 取得区间 0,200 上的最大值 100；
当 200所以当 t=300 时，ht 取得区间 200,300 上的最大值 87.5．
综上，由 100>87.5 可知，ht 在区间 0,300 上可以取得最大值 100，此时 t=50，即从二月一日开始的第 50 天时，上市的西红柿纯收益最大．
5. （1） 50 人．
（2） 该店最早可在 5 年后还清所有债务，此时消费品价格定为每件 55 元．
6. 分别以 AB，AD 所在直线为 x 轴，y 轴建立平面直角坐标系 xOy，如图（2）所示，
则 DC 的方程为 x2+y2=40≤x≤3,y>0，
设 Px,y0所以 V=πr2l=πx2π2⋅4-x2=14πx24-x2，即 V2=116π2x44-x2，
设 t=x2∈0,3，令 u=t24-t，则 uʹ=-3t2+8t=-3tt-83，
令 uʹ=0，得 t=83，
当 830，u 是增函数，
所以当 t=83 时，u 有极大值，也是最大值，
所以当 x=263 m 时，V 有最大值 439π m3，此时 y=4-x2=233 m，
故裁一个矩形，两边长分别为 263 m 和 233 m 时，能使圆柱的体积最大，其最大值为 439π m3．
7. 巨响发生在接报中心西偏北 45∘ 距中心 68010 m 处．
8. （1） 由题意知，点 M，N 的坐标分别为 5,40，20,2.5．
将其分别代入 y=ax2+b，得 a25+b=40,a400+b=2.5,
解得 a=1000,b=0.
（2） ①由（1）知，y=1000x25≤x≤20，
则点 P 的坐标为 t,1000t2．
设在点 P 处的切线 l 交 x，y 轴分别于点 A，B，yʹ=-2000x3，
则直线 l 的方程为 y-1000t2=-2000t3x-t，由此得 A3t2,0，B0,3000t2，
故 ft=3t22+3000t22=32t2+4×106t4，t∈5,20．
②设 gt=t2+4×106t4，
则 gʹt=2t-16×106t5．
令 gʹt=0，解得 t=102．
当 t∈5,102 时，gʹt<0，gt 单调递减；
当 t∈102,20 时，gʹt>0，gt 单调递增．
所以，当 t=102 时，函数 gt 有极小值，也是最小值，gtmin=300，此时 ftmin=153．
答：当 t=102 时，公路 l 的长度最短，最短长度为 153 km．
9. （1） 设抛物线的方程为：y=-ax2a>0，
则抛物线过点 10,-32，
代入抛物线方程解得：a=3200．
令 y=-6，
解得 x=±20，
则隧道设计的拱宽 l 是 40 m．
（2） 抛物线最大拱高为 h m，h≥6，
抛物线过点 10,-h-92，
代入抛物线方程得：a=h-92100，
令 y=-h，
则 -h-92100x2=-h，
解得：x2=100hh-92，
则 l22=100hh-92，h=92l2l2-400．
因为 h≥6，
所以 92l2l2-400≥6，
即 20 所以 S=23lh=23l⋅92l2l2-400=3l3l2-40020所以 Sʹ=9l2l2-400-3l3⋅2ll2-4002=3l2l2-1200l2-4002=3l2l+203l-203l2-4002.
当 20当 2030，S 在 203,40 上单调增．
所以 S 在 l=203 时取得最小值，
此时 l=203，h=274．
答：当拱高为 274 m，拱宽为 203 m 时，使得隧道口截面面积最小．
10. （1） 如图所示，以 O 为坐标原点，OC 所在直线为 x 轴，OA 所在直线为 y 轴，建立平面直角坐标系 xOy .
由条件知 A0,60，C170,0，直线 BC 的斜率 KBC=-tan∠BCO=-43 .
又因为 AB⊥BC ，所以直线 AB 的斜率 kAB=34 .
设点 B 的坐标 a,b，则 kBC=b-0a-170=-43，kAB=b-60a-0=34 ，
解得 a=80,b=120，所以 BC=170-802+0-1202=150 .
因此新桥 BC 的长是 150 m .
（2） 设保护区的边界圆 M 的半径为 rm，OM=dm0≤d≤60 .
由条件知，直线 BC 的方程为 y=-43x-170，即 4x+3y-680=0 .
由于圆 M 与直线 BC 相切，故点 M0,d 到直线 BC 的距离是 r ，
即 r=∣3d-680∣42+32=680-3d5 .
因为 O 和 A 到圆 M 上任意一点的距离均不少于 80 m，
所以 r-d≥80,r-60-d≥80, 即 680-3d5-d≥80,680-3d5-60-d≥80, 解得 10≤d≤35 .
故当 d=10 时，r=680-3d5 最大，即圆面积最大．
所以当 10 m 时，圆形保护区的面积最大．
11. （1） y=160πr-8πr2+4πcr2，定义域为 0,2．
（2） 当 392 时，建造费用
最小时 r=320c-2．
12. （1） 312 m3．
（2） 当 PO1=23 m 时，仓库的容积 V 取得最大值．
13. （1） S1=14a2sin2θ，S2=a2sin22θsin22θ+4sin2θ+4．
（2） S1S2min=94．
14. （1） 1040 m．
（2） 3537 min．
（3） 125043,62514m/min．
15. （1） 由题意，可得 AD=12 km．
由题可知 126-16v≤14，
解得 649≤v≤647．
（2） 方法一：经过 t h，甲、乙之间的距离的平方为 ft．
由于乙先到达 D 地，故 16v<2，即 v>8．
①当 0ft=6t2+vt2-2×6t×vt×cs∠DAB=v2-485v+36t2.
因为 v2-485v+36>0，
所以当 t=5v 时，ft 取得最大值，
所以 v2-485v+36×5v2≤25，
解得 v≥154．
②当 5ft=vt-1-6t2+9=v-62t-1v-62+9．
因为 v>8，
所以 1v-6<5v，v-62>0，
所以当 t=13v 时，ft 取得最大值，
所以 v-6213v-1v-62+9≤25，
解得 398≤v≤394．
③当 13≤vt≤16，13v≤t≤16v 时，ft=12-6t2+16-vt2，
因为 12-6t>0，16-vt>0，
所以 ft 在 13v,16v 上单调递减，
所以当 t=13v 时，ft 取得最大值，
12-6×13v2+16-v×13v2≤25，
解得 398≤v≤394．
因为 v>8，
所以 8方法二：设经过 t h，甲、乙之间的距离的平方为 ft．
由于乙先到达 D 地，故 16v<2，即 v>8．
以 A 为原点坐标，AD 为 x 轴建立平面直角坐标系．
①当 0由于 45vt-6t2+35vt2≤25，
所以 45v-62+35v2≤25t2 对任意 0所以 45v-62+35v2≤v2，
解得 v≥154．
②当 5由于 vt-1-6t2+32≤25，
所以 -4≤vt-1-6t≤4 对任意 5v即 v-6≤5t,-3t≤v-6 对任意 5v所以 v-6≤5v13,-3v13≤v-6,
解得 398≤v≤394．
③当 13≤vt≤16 时，即 13v≤t≤16v，此时 ft=12-6t2+16-vt2．
由①及②知 8于是 0<12-6t≤12-78v≤12-78394=4．
又因为 0≤16-vt≤3，
所以 ft=12-6t2+16-vt2≤42+33=25 恒成立．
综上①②③可知 816. （1） 当 1≤x≤137 时，gx>hx；
当 138≤x≤213 时，
gxfx=900kx,1≤x≤137,x∈N500k214-x,138≤x≤213,x∈N．
（2） 当 x=137 时完成任务用时最少．
17. （1） 到 2024 年底可全部还清贷款．
（2） 每生每年的最低收费标准为 992 元．
18. （1） x=a32．
（2） 16 年．
19. （1） x=80，y=50，p=0.4，q=0.25，补图略．
（2） 35．
20. （1） 设一根木条长为 x m，
则正方形的边长为 21-x22=4-x2 m．
因为 S四边形ABCD>14，
所以 4-x2>14，即 x<152．
又因为四根木条将圆分成 9 个区域，所以 x>2，
所以 42<4x<215．
答：木条总长的取值范围为 42,215．
（2） 方法一：
设 AB 所在木条的长为 a m，则 BC 所在木条的长为 3-am．
因为 a∈0,2，3-a∈0,2，
所以 a∈1,2，
S矩形ABCD=41-a24⋅1-3-a24=4-a2⋅4-3-a2=a4-6a3+a2+24a-20.
设 fa=a4-6a3+a2+24a-20，fʹa=4a3-18a2+2a+24=2a+12a-3a-4，
令 fʹa=0，得 a=32 或 a=-1（舍去）或 a=4（舍去）．
当 a 变化时，fʹa，fa 的变化情况如下表：
a1,323232,2fʹa+0-fa↗极大值↘
所以当 a=32 时，famax=f32=4916，即 Smax=74．
答：窗口 ABCD 面积的最大值为 74 m2．
方法二：
设 AB 所在木条的边长为 a m，BC 所在的木条的长为 b m．
由题意知 2a+2b=6，即 a+b=3．
因为 a,b∈0,2，
所以 b=3-a∈0,2，
从而 a,b∈1,2．
由于 AB=21-b24，BC=21-a24，
S矩形ABCD=41-b24⋅1-a24=4-b2⋅4-a2．
因为 4-b2⋅4-a2≤8-a2+b22≤8-a+b222=74，
当且仅当 a=b=32∈1,2 时，S矩形ABCD=74．
答：窗口 ABCD 面积的最大值为 74 m2．
21. （1） ①由题意知，在 Rt△O1PT 中，
∠O1PT=α，O1T=1，
所以 O1P=1sinα．
又 OO1=1,
所以 OP=1sinα+1．
在 Rt△OPQ 中，OQ=OPtanα=1+1sinαtanα=1+sinαcsα，
所以 Rt△OPQ 的面积为
S=12OP⋅OQ=121+1sinα1+sinαcsα=1+sinα22sinαcsα=1+sinα2sin2α0<α<π2.
②由题意得；OQ=OT=t，O1T=1，且 Rt△POQ∽Rt△PTO1，
所以 OPOQ=TPTO1，即 OPt=t2+OP2-t1，化简，得 OP=2t2t2-1t>1，
所以 Rt△OPQ 的面积为 S=12OQ⋅OP=12t⋅2t2t2-1=t3t2-1t>1．
（2） 选用（1）中①的函数关系 S=1+sinα2sin2α0<α<π2．
Sʹ=21+sinαcsαsin2α-21+sinα2cs2αsin22α=21+sinαcsαsin2α-1+sinαcs2αsin22α=21+sinαsin2α-α-1-2sin2αsin22α=21+sinα22sinα-1sin22α0<α<π2.
由 Sʹ=21+sinα22sinα-1sin22α=00<α<π2，得 α=π6.
当 α 变化时，Sʹ，S 的变化情况如下表：
α0,π6π6π6,π2Sʹ-0+S↘极小值↗
所以当 α=π6 时，△OPQ 的面积 S 取得最小值，且最小值为 1+sinπ62sin2×π6=332km2．
选用（1）中②的函数关系 S=t3t2-1t>1．
Sʹ=3t2t2-1-t3⋅2tt2-12=t2t+3t-3t2-12t>1．
由 Sʹ=t2t+3t-3t2-12=0t>1，得 t=3．
当 t 变化时，Sʹ，S 的变化如下表：
t1,333,+∞Sʹ-0+S↘极小值↗
所以当 t=3 时，△OPQ 的面积 S 取得最小值，且最小值为 3332-1=332km2．