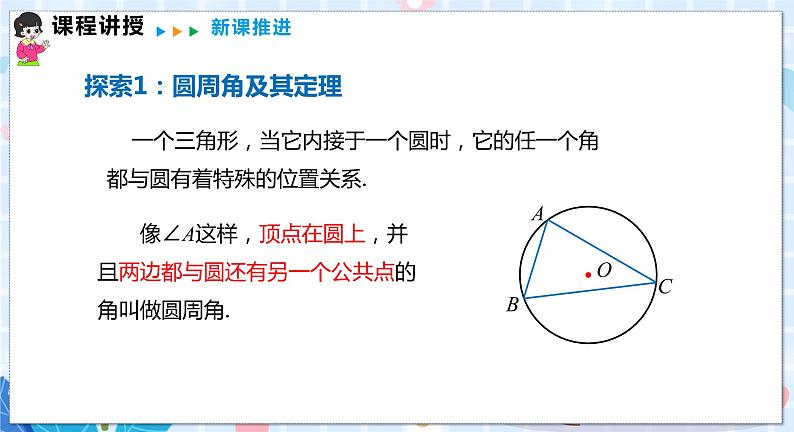
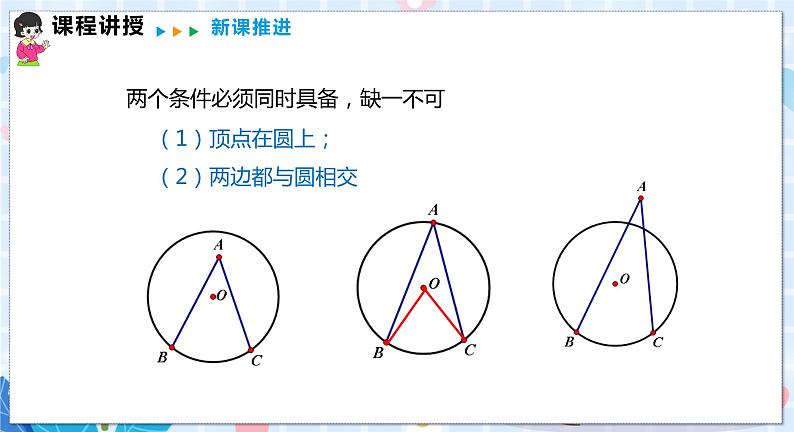
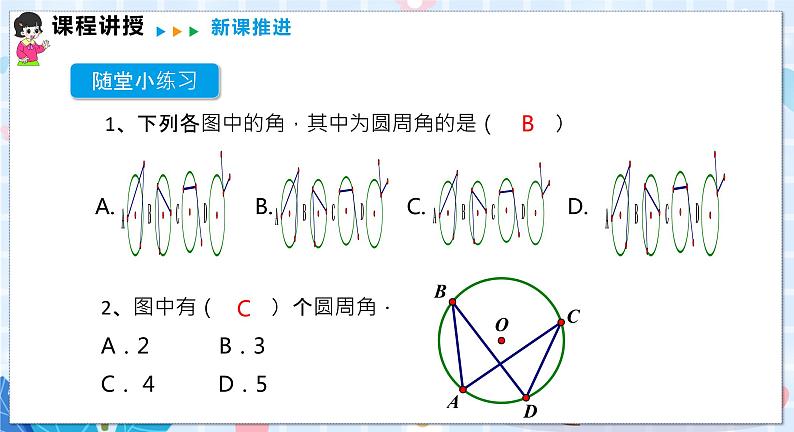
沪科版九年级下册24.3.1 圆周角定理教案配套ppt课件

这是一份沪科版九年级下册24.3.1 圆周角定理教案配套ppt课件，文件包含243第1课时圆周角定理及其推论pptx、243第1课时圆周角定理及其推论docx等2份课件配套教学资源，其中PPT共25页， 欢迎下载使用。
24.3　圆周角第1课时　圆周角定理及其推论 ◇教学目标◇ 【知识与技能】1.了解圆周角的概念,理解圆周角定理;2.熟练掌握圆周角定理及其推论,并灵活运用.【过程与方法】1.通过观察、比较、分析圆周角与圆心角的关系,发展学生合情推理和演绎推理的能力;通过引导学生添加合理的辅助线,培养学生的创造力.2.在探索圆周角定理的过程中,学会运用分类讨论和转化的数学思想解决问题;渗透由“特殊到一般”、由“一般到特殊”的数学思想.【情感、态度与价值观】引导学生对图形进行观察,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心.◇教学重难点◇【教学重点】圆周角定理及其推论.【教学难点】运用分类讨论的思想推理圆周角定理.◇教学过程◇一、情境导入如图所示,足球比赛中甲队员在圆心O处,乙队员在圆上C处,丙队员带球突破防守到圆上C处,依然把球传给了甲,你知道为什么吗?你能用数学知识解释一下吗?二、合作探究探究点1　识别圆周角,能利用圆周角定理及其推论求角的度数典例1　如图,☉O是△ABC的外接圆,且OB=BC.观察图形可知所对的圆心角是　　　　,所对的圆周角是　　　　.根据题意可知OB=OC=BC,所以△BOC是　　　　三角形,所以∠BOC的度数为　　　　.根据圆周角定理可知∠A=∠BOC=　　　　. [解析]　根据圆心角和圆周角的定义知,所对的圆心角是∠BOC,所对的圆周角是∠A,根据已知条件和圆周角定理知,∠A=∠BOC=30°.[答案]　∠BOC　∠A　等边　60°　30°【技巧点拨】求圆周角度数的思路:在圆内求圆周角要看圆周角所对的弧,找同弧或等弧所对的圆周角或圆心角进行转化.如果有直径,一般利用直径所对的圆周角是直角求解.探究点2　利用圆周角定理及其推论进行证明典例2　如图,以△ABC的边AB为直径作☉O交BC于点D,已知BD=CD.(1)求证:△ABC是等腰三角形;(2)若∠A=36°,求的度数.[解析]　(1)连接AD.∵AB是☉O的直径,∴∠ADB=90°,即AD⊥BC.又∵BD=CD,∴AD是线段BC的垂直平分线,∴AB=AC,∴△ABC是等腰三角形.(2)∵∠BAC=36°,AB=AC,∴∠B=∠C=(180°-∠BAC)÷2=72°,∴的度数为72°×2=144°. 如果题目的已知条件中有直径,往往作出直径所对的圆周角,简记为“见直径出直角”;如果需要直角或证明垂直,往往作出直径,简记为“需直角作直径”.变式训练　如图,☉O的直径AB=10,C为直径AB下方半圆上一点,∠ACB的平分线交☉O于点D,连接AD,BD.(1)判断△ABD的形状,并说明理由;(2)若弦AC=6,求BC的长.[解析]　(1)△ABD是等腰直角三角形.理由如下:∵AB为☉O的直径,∴∠ADB=90°.∵CD是∠ACB的平分线,∴,∴AD=BD,∴△ABD是等腰直角三角形.(2)∵AB为☉O的直径,∴∠ACB=90°.在Rt△ABC中,BC==8.三、板书设计圆周角定理及其推论圆周角◇教学反思◇在课堂训练和知识运用过程中,教师引导学生注重前后知识的联系,提高学生的综合运用能力,培养学生对数学的应用意识和创新意识.从教学过程分析,学生能够根据教师的引导,进行分类讨论和总结,借助多媒体教学,使学生更容易接受.