沪科版数学八年级下册 期末数学试卷 及答案解析5

这是一份沪科版数学八年级下册 期末数学试卷 及答案解析5，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
八年级（下）期末数学试卷
一、选择题（本题共10小题，每题3分，共30分．每小题有四个答案，其中有且只有一个答案是正确的，请把正确答案的代号，写在题后的括号内）
1．（3分）下列各式中与是同类二次根式的是（　　）
A． B． C． D．
2．（3分）下列运算正确的是（　　）
A．＝±5 B． C． D．
3．（3分）以下列长度（单位：cm）为三边，能构成直角三角形的是（　　）
A．1、2、3 B．、、 C．2、3、4 D．4、5、6
4．（3分）一元二次方程x2﹣4x+c＝0有两个相等的实数根，则c的值是（　　）
A．6 B．5 C．4 D．3
5．（3分）如图，在▱ABCD中，DE平分∠ADC，AD＝8，BE＝3，则AB的长是（　　）

A．3 B．8 C．11 D．5
6．（3分）我国政府为解决老百姓看病难的问题，决定下调药品的价格，某种药品经过两次降价后，由每盒60元下调至52元，若设每次平均降价的百分率为x，由题意可列方程为（　　）
A．60（1﹣x）+60（1﹣x）2＝52 B．60（1﹣2x）＝52
C．60（1﹣x）2＝52 D．60（1﹣x2）＝52
7．（3分）为了解体育锻炼情况，班主任从八（5）班45名同学中随机抽取8位同学开展“1分钟跳绳”测试，得分如下（满分15分）：15，10，13，13，8，12，13，12，则以下判断正确的是（　　）
A．这组数据的众数是13，说明全班同学的平均成绩达到13分
B．这组数据的中位数是12，说明12分以上的人数占大多数
C．这组数据的平均数是12，可以估计全班同学的平均成绩是12分
D．以上均不正确
8．（3分）已知x1、x2是一元二次方程x2﹣6x+3＝0的两个实数根，则的值为（　　）
A．4 B．﹣4 C． D．2
9．（3分）如图，在矩形ABCD中，连接AC，以点A为圆心，小于AD的长为半径画弧，分别交AD，AC于点E，F，分别以点E，F为圆心，大于的长为半径画弧，两弧在∠DAC内交于点G，作射线AG，交DC于点H．若AD＝6，AB＝8，则△AHC的面积为（　　）

A．24 B．30 C．15 D．9
10．（3分）如图，正方形ABCD中，AB＝3，点E在边CD上，若CD＝3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．则GF为（　　）

A． B． C． D．
二、填空题（本大题共5小题，每小题3分，满分15分）
11．（3分）要使代数式有意义，则实数x的取值范围是　 　．
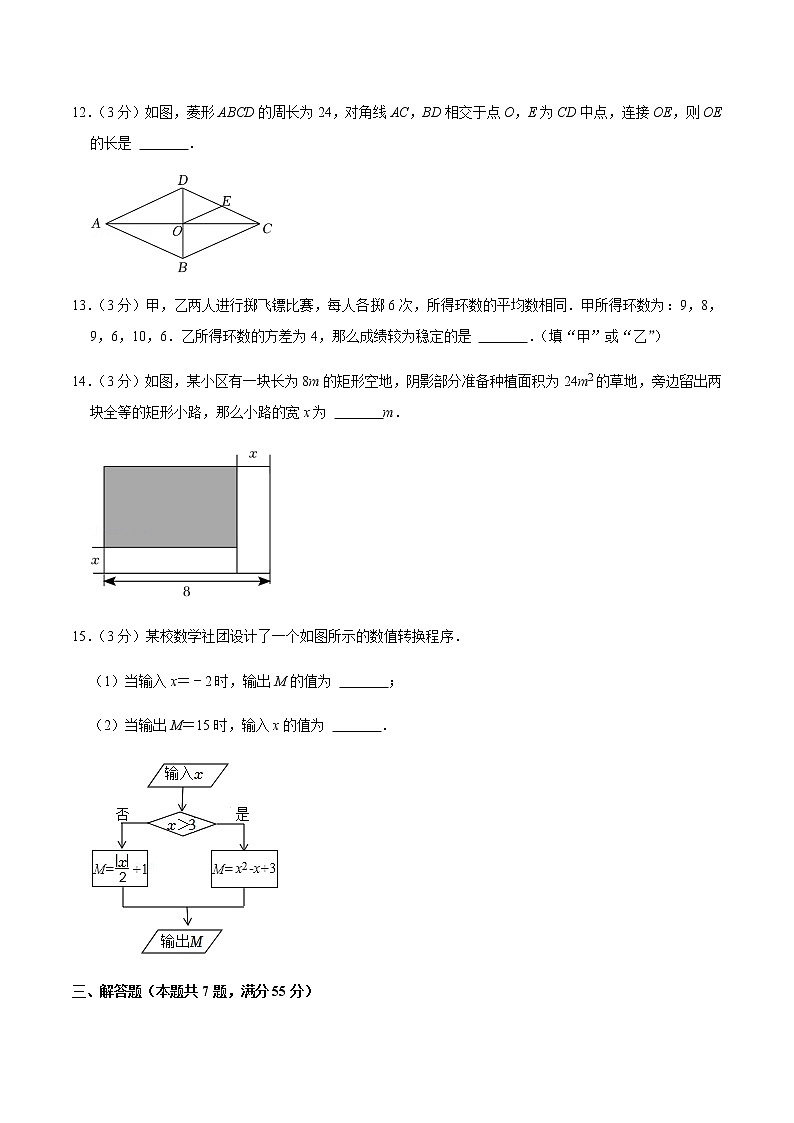
12．（3分）如图，菱形ABCD的周长为24，对角线AC，BD相交于点O，E为CD中点，连接OE，则OE的长是 　 　．

13．（3分）甲，乙两人进行掷飞镖比赛，每人各掷6次，所得环数的平均数相同．甲所得环数为：9，8，9，6，10，6．乙所得环数的方差为4，那么成绩较为稳定的是 　 　．（填“甲”或“乙”）
14．（3分）如图，某小区有一块长为8m的矩形空地，阴影部分准备种植面积为24m2的草地，旁边留出两块全等的矩形小路，那么小路的宽x为 　 　m．

15．（3分）某校数学社团设计了一个如图所示的数值转换程序．
（1）当输入x＝﹣2时，输出M的值为 　 　；
（2）当输出M＝15时，输入x的值为 　 　．

三、解答题（本题共7题，满分55分）
16．（5分）计算：．
17．（5分）解方程：x2﹣2x﹣3＝0．
18．（6分）某船从港口A出发沿南偏东32°方向航行15海里到达B岛，然后沿某方向航行20海里到达C岛，最后沿某个方向航行了25海里回到港口A，判断此时△ABC的形状，该船从B岛出发到C是沿哪个方向航行的，请说明理由．

19．（6分）如图是由边长为1的小正方形构成的6×4的网格，点A，B均在格点上，
（1）在图①中画出以AB为对角线的正方形ACBD，且点C和点D均在格点上；
（2）在图②中画出以AB为对角线且周长为的平行四边形AEBF，且点E和点F均在格点上．

20．（8分）如图，在四边形ABCD中，AD∥BC，AB＝AD，∠BAD的平分线AE交对角线BD于点F，交BC于点E．
（1）求证：四边形ABED是菱形；
（2）若BE＝EC，AE＝6，BD＝8，四边形AECD的面积．

21．（8分）某校为进一步提高教职工的身体素质，提倡“每天一万步”活动，校工会随机抽取20名教职工一天行走的步数，对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：
组别
步数分组
频数
频率
A
5500≤x＜6500
2
0.1
B
6500≤x＜7500
10
0.5
C
7500≤x＜8500
a
m
D
8500≤x＜9500
3
0.15
E
9500≤x＜10500
b
0.15
请根据以上信息解答下列问题：
（1）填空：a＝　 　，b＝　 　，m＝　 　，并补全频数分布直方图；
（2）这20名教职工一天行走步数的中位数落在 　 　组；
（3）若该校教职工共有320人，请估计其中一天行走步数不少于7500步的人数．

22．（8分）某水果店标价为10元/kg的某种水果经过两次降价且两次降价的百分率都是10%，请回答下列问题：
（1）该水果经过两次降价后的价格是 　 　元/kg；
（2）从第二次降价的第1天算起，第x天（x为整数）的销量及储藏和损耗费用的相关信息如下表所示，已知该水果的进价为4.1元/kg，设销售该水果第x天（1≤x＜10）的利润为368元，求x的值．
时间/天
x
销量/kg
120﹣2x
储藏和损耗费用/元
3x2﹣68x+409
23．（9分）如图，在矩形ABCD中，E是BC上一动点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，AB＝3，AD＝4．
（1）如图1，当∠DAG＝30°时，求BE的长；
（2）如图2，当点E是BC的中点时，求线段GC的长；
（3）如图3，点E在运动过程中，当△CFE的周长最小时，直接写出BE的长．


八年级（下）期末数学试卷
参考答案与试题解析
一、选择题（本题共10小题，每题3分，共30分．每小题有四个答案，其中有且只有一个答案是正确的，请把正确答案的代号，写在题后的括号内）
1．（3分）下列各式中与是同类二次根式的是（　　）
A． B． C． D．
【解答】解：A.＝3；不符合题意．
B.＝2；符合题意．
C.＝3；不符合题意．
D.＝；不符合题意．
故选：B．
2．（3分）下列运算正确的是（　　）
A．＝±5 B． C． D．
【解答】解：A选项：，所以A选项错误．
B选项：3＝2，所以B选项错误．
C选项：，所以C选项错误．
D选项：＝2＝6，所以D选项正确．
故选：D．
3．（3分）以下列长度（单位：cm）为三边，能构成直角三角形的是（　　）
A．1、2、3 B．、、 C．2、3、4 D．4、5、6
【解答】解：A、∵1+2＝3，
∴1，2，3不能组成三角形，
故A不符合题意；
B、∵（）2+（）2＝3，（）2＝3，
∴2+（）2＝（）2，
∴，，能作为直角三角形三边长，
故B符合题意；
C、∵22+32＝13，42＝16，
∴22+32≠42，
∴2，3，4不能作为直角三角形三边长，
故C不符合题意；
D、∵42+52＝41，62＝36，
∴42+52≠62，
∴4，5，6不能作为直角三角形三边长，
故D不符合题意；
故选：B．
4．（3分）一元二次方程x2﹣4x+c＝0有两个相等的实数根，则c的值是（　　）
A．6 B．5 C．4 D．3
【解答】解：∵一元二次方程x2﹣4x+c＝0有两个相等的实数根，
∴Δ＝（﹣4）2﹣4c＝0，
∴16﹣4c＝0，
∴c＝4，
故选：C．
5．（3分）如图，在▱ABCD中，DE平分∠ADC，AD＝8，BE＝3，则AB的长是（　　）

A．3 B．8 C．11 D．5
【解答】解：在▱ABCD中，AD＝8，
∴BC＝AD＝8，AD∥BC，
∴CE＝BC﹣BE＝8﹣3＝5，∠ADE＝∠CED，
∵DE平分∠ADC，
∴∠ADE＝∠CDE，
∴∠CDE＝∠CED，
∴CD＝CE＝5＝AB，
故选：D．
6．（3分）我国政府为解决老百姓看病难的问题，决定下调药品的价格，某种药品经过两次降价后，由每盒60元下调至52元，若设每次平均降价的百分率为x，由题意可列方程为（　　）
A．60（1﹣x）+60（1﹣x）2＝52 B．60（1﹣2x）＝52
C．60（1﹣x）2＝52 D．60（1﹣x2）＝52
【解答】解：设平均每次下调的百分率为x，
第一次下调到60（1﹣x%），
第二次下调到60（1﹣x%）（1﹣x%），
∴60（1﹣x）2＝52．
故选：C．
7．（3分）为了解体育锻炼情况，班主任从八（5）班45名同学中随机抽取8位同学开展“1分钟跳绳”测试，得分如下（满分15分）：15，10，13，13，8，12，13，12，则以下判断正确的是（　　）
A．这组数据的众数是13，说明全班同学的平均成绩达到13分
B．这组数据的中位数是12，说明12分以上的人数占大多数
C．这组数据的平均数是12，可以估计全班同学的平均成绩是12分
D．以上均不正确
【解答】解：A．这组数据的众数是13，而全班同学的平均成绩达到12，故本选项不合题意；
B．这组数据的中位数是12，说明12分以上的人数占一半，故本选项不合题意；
C．这组数据的平均数是12，可以估计全班同学的平均成绩是12分，说法正确，故本选项符合题意；
D．选项C正确，故本选项不合题意；
故选：C．
8．（3分）已知x1、x2是一元二次方程x2﹣6x+3＝0的两个实数根，则的值为（　　）
A．4 B．﹣4 C． D．2
【解答】解：根据题意得x1+x2＝6，x1x2＝3，
则＝＝＝4，
故选：A．
9．（3分）如图，在矩形ABCD中，连接AC，以点A为圆心，小于AD的长为半径画弧，分别交AD，AC于点E，F，分别以点E，F为圆心，大于的长为半径画弧，两弧在∠DAC内交于点G，作射线AG，交DC于点H．若AD＝6，AB＝8，则△AHC的面积为（　　）

A．24 B．30 C．15 D．9
【解答】解：过H点作HM⊥AC，如图，
由作法得AH平分∠DAC，
∴DH＝MH，
∵四边形ABCD为矩形，
∴CD＝AB＝8，
在Rt△ADC中，AC＝＝10，
在Rt△ADH和Rt△AMH中，
，
∴Rt△ADH≌Rt△AMH（HL），
∴AM＝AD＝6，
∴CM＝AC﹣AM＝10﹣6＝4，
设CH＝x，则DH＝HM＝8﹣x，
在Rt△CHM中，（8﹣x）2+42＝x2，
解得x＝5，
∴△AHC的面积＝CH•AD＝×5×6＝15．
故选：C．

10．（3分）如图，正方形ABCD中，AB＝3，点E在边CD上，若CD＝3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．则GF为（　　）

A． B． C． D．
【解答】解：在正方形ABCD中，AB＝3，CD＝3DE，
∴DE＝×3＝1，CE＝3﹣1＝2，
∵△ADE沿AE对折至△AFE，
∴AD＝AF，EF＝DE＝1，∠AFE＝∠D＝90°，
∴AB＝AF＝AD，
在Rt△ABG和Rt△AFG中，
，
∴Rt△ABG≌Rt△AFG（HL），
∴BG＝FG，
设BG＝FG＝x，则EG＝EF+FG＝1+x，CG＝3﹣x，
在Rt△CEG中，EG2＝CG2+CE2，
即（1+x）2＝（3﹣x）2+22，
解得x＝，
∴GF＝．
故选：B．
二、填空题（本大题共5小题，每小题3分，满分15分）
11．（3分）要使代数式有意义，则实数x的取值范围是　x≥﹣2　．
【解答】解：由题意可知：x+2≥0，
∴x≥﹣2
故答案是：x≥﹣2．
12．（3分）如图，菱形ABCD的周长为24，对角线AC，BD相交于点O，E为CD中点，连接OE，则OE的长是 　3　．

【解答】解：∵菱形ABCD的周长为24，
∴CD＝BC＝＝6，且O为BD的中点，
∵E为CD的中点，
∴OE为△BCD的中位线，
∴OE＝CB＝3，
故答案为：3．
13．（3分）甲，乙两人进行掷飞镖比赛，每人各掷6次，所得环数的平均数相同．甲所得环数为：9，8，9，6，10，6．乙所得环数的方差为4，那么成绩较为稳定的是 　甲　．（填“甲”或“乙”）
【解答】解：甲组数据的平均数＝（9+8+9+6+10+6）÷6＝8，
甲组数据的方差S2＝×[2×（9﹣8）2+2×（6﹣8）2+（8﹣8）2+（10﹣8）2]＝，
∵S2甲＜S2乙，
∴成绩较为稳定的是甲．
故答案为：甲．
14．（3分）如图，某小区有一块长为8m的矩形空地，阴影部分准备种植面积为24m2的草地，旁边留出两块全等的矩形小路，那么小路的宽x为 　2　m．

【解答】解：由题可得，阴影部分的长为（8﹣x）m，宽为（8﹣2x）m，
∵阴影部分的面积为24m2，
∴（8﹣x）（8﹣2x）＝24，
解得x1＝2，x2＝10（不合题意，舍去），
∴小路的宽x为2m，
故答案为：2．
15．（3分）某校数学社团设计了一个如图所示的数值转换程序．
（1）当输入x＝﹣2时，输出M的值为 　2　；
（2）当输出M＝15时，输入x的值为 　﹣28或4　．

【解答】解：（1）∵x＝﹣2＜3，
∴M＝+1＝1+1＝2，
故答案为：2；
（2）∵M＝15，
∴+1＝15（x≤3）或x2﹣x+3＝15（x＞3），
解得x＝﹣28或x＝4，
∴输入的x的值为﹣28或4，
故答案为：﹣28或4．
三、解答题（本题共7题，满分55分）
16．（5分）计算：．
【解答】解：原式＝2+3
＝5
＝．
17．（5分）解方程：x2﹣2x﹣3＝0．
【解答】解：原方程可以变形为（x﹣3）（x+1）＝0
x﹣3＝0或x+1＝0
∴x1＝3，x2＝﹣1．
18．（6分）某船从港口A出发沿南偏东32°方向航行15海里到达B岛，然后沿某方向航行20海里到达C岛，最后沿某个方向航行了25海里回到港口A，判断此时△ABC的形状，该船从B岛出发到C是沿哪个方向航行的，请说明理由．

【解答】解：该船从B岛出发到C是沿西偏南32°方向航行的．
理由：由题意得：AB＝15海里，BC＝20海里，AC＝25海里，
∵152+202＝252，
∴△ABC为直角三角形，且∠ABC＝90°，
由题意得∠BAD＝32°，∠ADB＝90°，

∴∠ABD＝90°﹣32°＝58°，
∴∠CBD＝90°﹣58°＝32°，
故该船从B岛出发到C是沿西偏南32°方向航行的．
19．（6分）如图是由边长为1的小正方形构成的6×4的网格，点A，B均在格点上，
（1）在图①中画出以AB为对角线的正方形ACBD，且点C和点D均在格点上；
（2）在图②中画出以AB为对角线且周长为的平行四边形AEBF，且点E和点F均在格点上．

【解答】解：（1）如图①中，正方形ACBD即为所求；
（2）如图②中，平行四边形AEBF即为所求．

20．（8分）如图，在四边形ABCD中，AD∥BC，AB＝AD，∠BAD的平分线AE交对角线BD于点F，交BC于点E．
（1）求证：四边形ABED是菱形；
（2）若BE＝EC，AE＝6，BD＝8，四边形AECD的面积．

【解答】（1）证明：∵AD∥BC，
∴∠DAE＝∠BEA，
∵AE平分∠BAD，
∴∠DAE＝∠BAE，
∴∠BEA＝∠BAE，
∴AB＝EB，
∵AB＝AD，
∴AD＝EB，
∵AD∥EB，
∴四边形ABED是平行四边形，
又∵AB＝AD，
∴平行四边形ABED是菱形；
（2）解：由（1）可知，AD＝BE，四边形ABED是菱形，
∴S菱形ABED＝AE•BD＝×6×8＝24，
∵BE＝EC，
∴AD＝EC，
∵AD∥BC，
∴四边形AECD是平行四边形，
∴S平行四边形AECD＝S菱形ABED＝24．
21．（8分）某校为进一步提高教职工的身体素质，提倡“每天一万步”活动，校工会随机抽取20名教职工一天行走的步数，对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：
组别
步数分组
频数
频率
A
5500≤x＜6500
2
0.1
B
6500≤x＜7500
10
0.5
C
7500≤x＜8500
a
m
D
8500≤x＜9500
3
0.15
E
9500≤x＜10500
b
0.15
请根据以上信息解答下列问题：
（1）填空：a＝　2　，b＝　3　，m＝　0.1　，并补全频数分布直方图；
（2）这20名教职工一天行走步数的中位数落在 　B　组；
（3）若该校教职工共有320人，请估计其中一天行走步数不少于7500步的人数．

【解答】解：（1）样本容量为2÷0.1＝20，
∴b＝20×0.15＝3，
则a＝20﹣（2+10+3+3）＝2，
∴m＝2÷20＝0.1，
补全图形如下：

故答案为：2、3、0.1；
（2）这20名教职工一天行走步数的中位数是第10、11个数据的平均数，而这两个数据均落在B组，
所以这20名教职工一天行走步数的中位数落在B组，
故答案为：B．
（3）估计其中一天行走步数不少于7500步的有320×（0.1+0.15+0.15）＝128（人）．
22．（8分）某水果店标价为10元/kg的某种水果经过两次降价且两次降价的百分率都是10%，请回答下列问题：
（1）该水果经过两次降价后的价格是 　8.1　元/kg；
（2）从第二次降价的第1天算起，第x天（x为整数）的销量及储藏和损耗费用的相关信息如下表所示，已知该水果的进价为4.1元/kg，设销售该水果第x天（1≤x＜10）的利润为368元，求x的值．
时间/天
x
销量/kg
120﹣2x
储藏和损耗费用/元
3x2﹣68x+409
【解答】解：（1）根据题意得：
10（1﹣10%）2＝8.1（元/千克）
故答案为：8.1．
（2）依题意得：（8.1﹣4.1）（120﹣x）﹣（3x2﹣64x+409）＝368，
整理得：x2﹣20x+99＝0．
解得：x1＝9，x2＝11．
又∵1≤x＜10，
∴x＝9．
答：x的值为9．
23．（9分）如图，在矩形ABCD中，E是BC上一动点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，AB＝3，AD＝4．
（1）如图1，当∠DAG＝30°时，求BE的长；
（2）如图2，当点E是BC的中点时，求线段GC的长；
（3）如图3，点E在运动过程中，当△CFE的周长最小时，直接写出BE的长．

【解答】解：（1）∵四边形ABCD是矩形，
∴∠BAD＝90°，
∵∠DAG＝30°，
∴∠BAG＝60°
由折叠知，∠BAE＝∠BAG＝30°，
在Rt△BAE中，∠BAE＝30°，AB＝3，
∴BE＝
（2）如图，连接GE，
∵E是BC的中点，
∴BE＝EC，
∵△ABE沿AE折叠后得到△AFE，
∴BE＝EF，
∴EF＝EC，
∵在矩形ABCD中，
∴∠C＝90°，
∴∠EFG＝90°，
∵在Rt△GFE和Rt△GCE中，，
∴Rt△GFE≌Rt△GCE（HL），
∴GF＝GC；
设GC＝x，则AG＝3+x，DG＝3﹣x，
在Rt△ADG中，42+（3﹣x）2＝（3+x）2，
解得x＝．
（3）如图1，
由折叠知，∠AFE＝∠B＝90°，EF＝BE，
∴EF+CE＝BE+CE＝BC＝AD＝4，
∴当CF最小时，△CEF的周长最小，
而当CF⊥EF时，CF最小，
即：∠CFE＝90°，
∵∠AFE＝90°，
∴∠AFE+∠CFE＝180°，
∴点A，F，C在同一条直线上时，CF最小，
由折叠知，AF＝AB＝3，
在Rt△ABC中，AB＝3，BC＝AD＝4，
∴AC＝5，
∴CF＝AC﹣AF＝2，
在Rt△CEF中，EF2+CF2＝CE2，
∴BE2+CF2＝（4﹣BE）2，
∴BE2+22＝（4﹣BE）2，
∴BE＝．