初中数学沪科版九年级下册24.1.3 中心对称图形教学演示课件ppt

这是一份初中数学沪科版九年级下册24.1.3 中心对称图形教学演示课件ppt，文件包含241第3课时平面直角坐标系中的旋转变换pptx、241第3课时平面直角坐标系中的旋转变换docx等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。
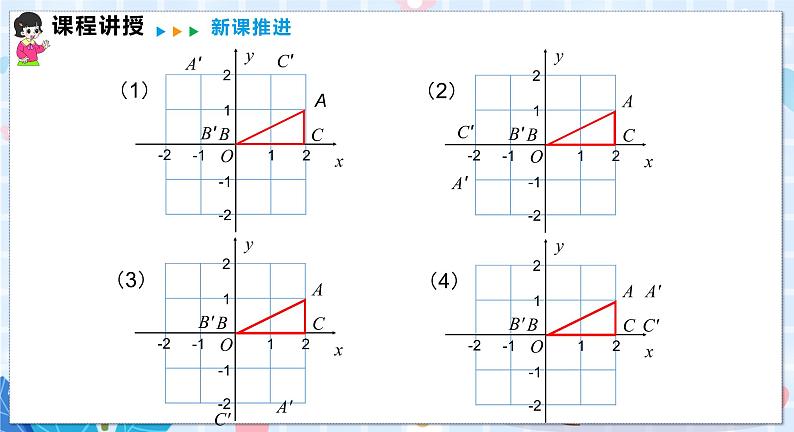
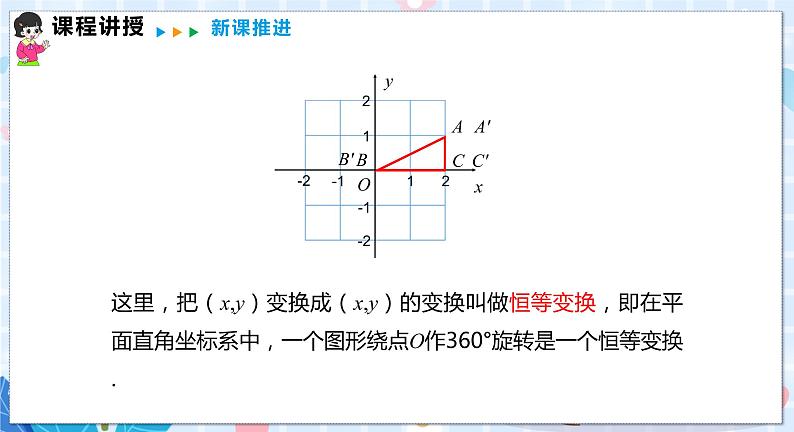
第3课时　平面直角坐标系中的旋转变换 ◇教学目标◇ 【知识与技能】1.理解并掌握旋转变化的特点,能够解决坐标平面内的旋转变换问题;2.能够运用旋转、轴对称或平移进行简单的图案设计.【过程与方法】鼓励学生动手操作,进一步加深学生对旋转的认识.【情感、态度与价值观】在教学中培养学生的动手操作能力以及合作交流意识.◇教学重难点◇【教学重点】能够解决平面直角坐标系中的旋转变化问题.【教学难点】利用旋转、轴对称或平移进行简单的图案设计.◇教学过程◇一、情境导入如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).分别画出△ABC以点O(0,0)为旋转中心,在图1中旋转90°、在图2中旋转180°、在图3中旋转270°、在图4中旋转360°而得到的△A'B'C'.(按逆时针方向旋转)图1　　　　　图2图3　　　　　图4二、合作探究探究点1　坐标平面内的旋转变换典例1　如图,在方格纸上建立的平面直角坐标系中,将△ABC绕点O按顺时针方向旋转90°,得△A'B'O,则点A'的坐标为              (　　)A.(3,1) B.(3,2)C.(2,3) D.(1,3)[解析]　根据网格结构找出点A,B旋转后的对应点A',B'的位置,然后与点O顺次连接即可,再根据平面直角坐标系写出点A'的坐标.如图,点A'的坐标为(1,3),故选D. 本题考查了坐标与图形旋转,根据网格结构作出旋转后的三角形,利用数形结合的思想求解.典例2　如图,在平面直角坐标系中,点B的坐标是(1,0),若点A的坐标为(a,b),将线段BA绕点B顺时针旋转90°得到线段BA',则点A'的坐标是　　　　. [解析]　过点A作AC⊥x轴,过点A'作A'D⊥x轴,垂足分别为C,D,易证Rt△ABC≌Rt△BA'D.∵点A的坐标为(a,b),点E的坐标是(1,0),∴OD=OB+BD=OB+AC=1+b,A'D=BC=OC-OB=a-1.∵点A'在第四象限,∴A'的坐标是(b+1,-a+1). 本题考查了坐标与线段的变化,作出全等三角形,利用全等三角形对应边相等求出点A'到坐标轴的距离是解题的关键,书写坐标时要注意点所在的象限.探究点2　图案设计典例3　用四块如图1所示的正方形卡片拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图2、图3、图4中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).图1　　　图2　　　　图3　　　　图4　[解析]　解法不唯一,例如:典例4　如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、对称或旋转变换,设计一个精美图案,使其满足:①既是轴对称图形,又是以点O为对称中心的中心对称图形;②所作图案用阴影标识,且阴影部分面积为4.[解析]　所给左上角的三角形的面积为×1×1=,故设计图案总共需要三角形4÷=8(个),以O为对称中心的中心对称图形,同时又是轴对称图形的设计方案有很多.[答案]　答案不唯一,以下各图供参考: 在读清要求后,进行方案的尝试设计后,一般要经历一个不断修改的过程,使问题在修正中得以解决.三、板书设计平面直角坐标系中的旋转变换1.坐标平面内的旋转变换2.图案设计◇教学反思◇教学过程中,强调学生自主探索和合作交流,鼓励学生自己动手操作,经历运用平移、旋转、轴对称的组合进行简单的图案设计过程,体会图形的欣赏与设计的奇妙.