






还剩9页未读,
继续阅读
所属成套资源:沪科版数学七上课件PPT整套
成套系列资料,整套一键下载
1.1.2 有理数的分类(课件)-2022-2023学年七年级数学上册同步精品课件(沪科版)
展开
这是一份1.1.2 有理数的分类(课件)-2022-2023学年七年级数学上册同步精品课件(沪科版),共17页。
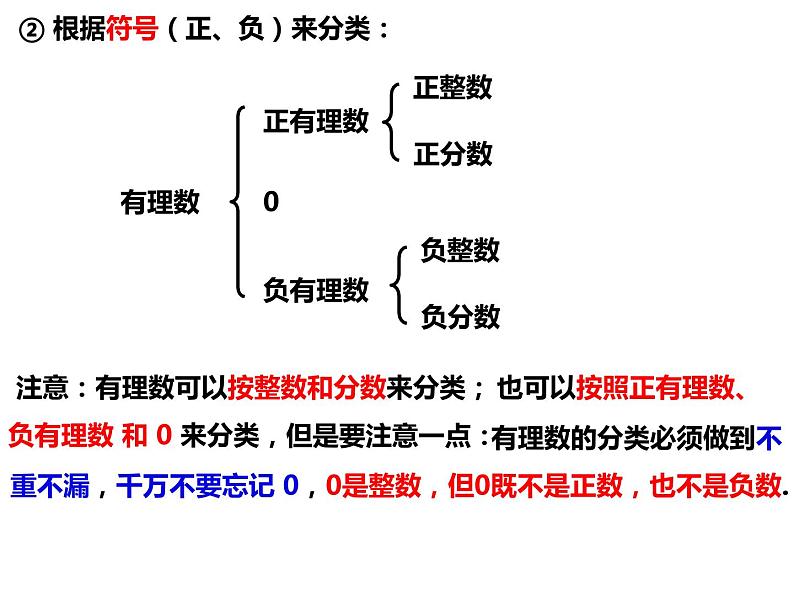
1.1.2 有理数的分类一、正数与负数的概念注:数0既不是正数,也不是负数。① 在计数时,数0可以表示没有,如0个. “0”的意义: ② 0还常用来表示某种量的基准,例如0℃不能理解成没有温度,它是实际温度为冰点时的的计量结果,用来作为计量温度的基准.③ 0比任何正数小,比任何负数大,它是正数与负数的分界.二、用正数和负数可以表示具有相反意义的量 用正数和负数可以表示具有相反意义的量。首先要确定一个基准,然后规定某种意义的量为正,则具有其相反意义的量为负。知识回顾 引入负数后,整数除了小学学过的整数外,还包含其它的整数吗?分数除了小学学过的分数外,还包含其它的分数吗? 问题:到目前为止,你已经认识了哪些类型的数?我们以前学过的数,像1,2,3,…称为称为正分数.,,正整数;那么在以上这些数的前面添上“-”号后,-1,-2,-3,…称为 负整数;-,-,-,…称为负分数.特别提示:0 既不是正数,也不是负数!问题:对于小数呢? 有限小数、无限循环小数、百分数都可以化为分数,因此这些小数应看做分数。导入新课概念归纳引入负数后,数的范围扩大了,整数包括分数包括整数和分数统称有理数.正整数、0和负整数,正分数和负分数.有理数整数分数正整数0负整数正分数负分数问题:你能根据有理数的定义对有理数进行分类吗?① 根据有理数的定义分类:例 2 把下面各数分别填入相应的框里:-16,0.04, ,- ,+32,0,-3.6,-4.5,+0.9.解:正数负数-16,0.04, ,+32- ,-3.6,-4.5.+0.9.交流: 1、例2中,数0能放入正数框或负数框里吗?2、你认为有理数还可以怎样分类?② 根据符号(正、负)来分类:有理数正有理数负有理数0正整数正分数负整数负分数 注意:有理数可以按整数和分数来分类; 也可以按照正有理数、负有理数 和 0 来分类, 有理数的分类必须做到不重不漏,千万不要忘记 0,0是整数,但0既不是正数,也不是负数. 但是要注意一点:1、下列说法正确的有( ) ① 整数就是正整数和负整数; ② 零是整数,但不是自然数; ③ 分数包括正分数、负分数; ④ 正数和负数统称有理数; ⑤ 一个有理数,它不是整数就是分数.A.1个 B.2个 C.3个 D.4个B巩固练习2、在下列表格内相应的空格里打“√”. 20200-π4.9-√√√√√√√√√√√√√√√√巩固练习 ② 到现在为止,我们学过的数(π 和无限不循环小数除外)都是有理数. 方法点拨:① 有限小数、无限循环小数、百分数都可以化为分数,因此这些数都是有理数.4、下列各数中,既是分数又是正数的是( )A.+2 B.+4 C.0 D.-2.3 3、有理数 -5,0,31,- ,1.2, ,4,-0.13 中,负分数有( )CA.5个 B.4个 C.2个 D.3个B巩固练习5、把下列各数填入如图所示的圈中(中间也要填).-6,10,0,25%,- ,3.14,-5.3, .正数分数负数整数1025%3.14-5.3-6010-5.3巩固练习6、把下列各数分别填入相应的括号内.-2,0,0.314,25%,11, ,-3 ,0.3,1 .·整数:{ }分数:{ }自然数:{ }非负数:{ }非正有理数:{ }-2,0,110.314,25%, ,-3 ,0.3,10,110,0.314,25%,11, ,0.3,1·方法点拨:非负数是指不是负数,即 正数和0.思考:非负整数是指哪些数?非正整数呢?正整数和零负整数和零-2,0,-3巩固练习7、在小学我们学习了偶数0,2,4,6,8,…,以及奇数1,3,5,7,9,…,现在我们学过了负数,也知道了负偶数与负奇数,负偶数-2,-4,-6,-8,…,负奇数-1,-3,-5,-7,…,下面我们将这些负偶数与负奇数排列如图所示:在上述的这些数中,观察它们的规律,并求-101在哪一列.解:-101在第四列.巩固练习8、观察下面一列数:-1,2,-3,4,-5,6,-7,…将这列数排成下列形式: 按照上述规律排下去,那么第10行从左边数第10个数是 ;数-203是第 行从左边数第 个数.-91157巩固练习9、把几个数用大括号括起来,中间用逗号断开,如:{1,2,3},{-2,7,8,19},我们称之为集合,称其中的数为集合的元素.如果一个集合满足:当有理数 a 是集合的元素时,有理数 8-a 也必是这个集合的元素,这样的集合我们称为“好集合”. (1) 请你判断集合{1,2},{1,4,7}是不是“好集合”; (2) 请你写出满足条件的两个“好集合”.巩固练习10、观察下面的一列数: ,- , ,- , ,- ,···请找出其中排列的规律,解答:(1) 第11个数是 ,第12个数是 .(2) 第2018个数是多少?(3) 如果这一组数据无线排列下去,与哪两个数越来越接近?-解:(2) 第2018个数是-(3) 如果这一组数据无线排列下去,与 0 或 -1 越来越接近.巩固练习本节课你有什么收获? 注意:有理数可以按整数和分数来分类; 也可以按照正有理数、负有理数 和 0 来分类,一、有理数的概念二、有理数的分类: 整数和分数统称有理数. 方法点拨:① 有限小数、无限循环小数、百分数都可以化为分数,因此这些数都是有理数. ② 到现在为止,我们学过的数(π 和无限不循环小数除外)都是有理数.有理数整数分数正整数0负整数正分数负分数有理数正有理数负有理数0正整数正分数负整数负分数 有理数的分类必须做到不重不漏,千万不要忘记 0,0是整数,但0既不是正数,也不是负数. 但是要注意一点:
1.1.2 有理数的分类一、正数与负数的概念注:数0既不是正数,也不是负数。① 在计数时,数0可以表示没有,如0个. “0”的意义: ② 0还常用来表示某种量的基准,例如0℃不能理解成没有温度,它是实际温度为冰点时的的计量结果,用来作为计量温度的基准.③ 0比任何正数小,比任何负数大,它是正数与负数的分界.二、用正数和负数可以表示具有相反意义的量 用正数和负数可以表示具有相反意义的量。首先要确定一个基准,然后规定某种意义的量为正,则具有其相反意义的量为负。知识回顾 引入负数后,整数除了小学学过的整数外,还包含其它的整数吗?分数除了小学学过的分数外,还包含其它的分数吗? 问题:到目前为止,你已经认识了哪些类型的数?我们以前学过的数,像1,2,3,…称为称为正分数.,,正整数;那么在以上这些数的前面添上“-”号后,-1,-2,-3,…称为 负整数;-,-,-,…称为负分数.特别提示:0 既不是正数,也不是负数!问题:对于小数呢? 有限小数、无限循环小数、百分数都可以化为分数,因此这些小数应看做分数。导入新课概念归纳引入负数后,数的范围扩大了,整数包括分数包括整数和分数统称有理数.正整数、0和负整数,正分数和负分数.有理数整数分数正整数0负整数正分数负分数问题:你能根据有理数的定义对有理数进行分类吗?① 根据有理数的定义分类:例 2 把下面各数分别填入相应的框里:-16,0.04, ,- ,+32,0,-3.6,-4.5,+0.9.解:正数负数-16,0.04, ,+32- ,-3.6,-4.5.+0.9.交流: 1、例2中,数0能放入正数框或负数框里吗?2、你认为有理数还可以怎样分类?② 根据符号(正、负)来分类:有理数正有理数负有理数0正整数正分数负整数负分数 注意:有理数可以按整数和分数来分类; 也可以按照正有理数、负有理数 和 0 来分类, 有理数的分类必须做到不重不漏,千万不要忘记 0,0是整数,但0既不是正数,也不是负数. 但是要注意一点:1、下列说法正确的有( ) ① 整数就是正整数和负整数; ② 零是整数,但不是自然数; ③ 分数包括正分数、负分数; ④ 正数和负数统称有理数; ⑤ 一个有理数,它不是整数就是分数.A.1个 B.2个 C.3个 D.4个B巩固练习2、在下列表格内相应的空格里打“√”. 20200-π4.9-√√√√√√√√√√√√√√√√巩固练习 ② 到现在为止,我们学过的数(π 和无限不循环小数除外)都是有理数. 方法点拨:① 有限小数、无限循环小数、百分数都可以化为分数,因此这些数都是有理数.4、下列各数中,既是分数又是正数的是( )A.+2 B.+4 C.0 D.-2.3 3、有理数 -5,0,31,- ,1.2, ,4,-0.13 中,负分数有( )CA.5个 B.4个 C.2个 D.3个B巩固练习5、把下列各数填入如图所示的圈中(中间也要填).-6,10,0,25%,- ,3.14,-5.3, .正数分数负数整数1025%3.14-5.3-6010-5.3巩固练习6、把下列各数分别填入相应的括号内.-2,0,0.314,25%,11, ,-3 ,0.3,1 .·整数:{ }分数:{ }自然数:{ }非负数:{ }非正有理数:{ }-2,0,110.314,25%, ,-3 ,0.3,10,110,0.314,25%,11, ,0.3,1·方法点拨:非负数是指不是负数,即 正数和0.思考:非负整数是指哪些数?非正整数呢?正整数和零负整数和零-2,0,-3巩固练习7、在小学我们学习了偶数0,2,4,6,8,…,以及奇数1,3,5,7,9,…,现在我们学过了负数,也知道了负偶数与负奇数,负偶数-2,-4,-6,-8,…,负奇数-1,-3,-5,-7,…,下面我们将这些负偶数与负奇数排列如图所示:在上述的这些数中,观察它们的规律,并求-101在哪一列.解:-101在第四列.巩固练习8、观察下面一列数:-1,2,-3,4,-5,6,-7,…将这列数排成下列形式: 按照上述规律排下去,那么第10行从左边数第10个数是 ;数-203是第 行从左边数第 个数.-91157巩固练习9、把几个数用大括号括起来,中间用逗号断开,如:{1,2,3},{-2,7,8,19},我们称之为集合,称其中的数为集合的元素.如果一个集合满足:当有理数 a 是集合的元素时,有理数 8-a 也必是这个集合的元素,这样的集合我们称为“好集合”. (1) 请你判断集合{1,2},{1,4,7}是不是“好集合”; (2) 请你写出满足条件的两个“好集合”.巩固练习10、观察下面的一列数: ,- , ,- , ,- ,···请找出其中排列的规律,解答:(1) 第11个数是 ,第12个数是 .(2) 第2018个数是多少?(3) 如果这一组数据无线排列下去,与哪两个数越来越接近?-解:(2) 第2018个数是-(3) 如果这一组数据无线排列下去,与 0 或 -1 越来越接近.巩固练习本节课你有什么收获? 注意:有理数可以按整数和分数来分类; 也可以按照正有理数、负有理数 和 0 来分类,一、有理数的概念二、有理数的分类: 整数和分数统称有理数. 方法点拨:① 有限小数、无限循环小数、百分数都可以化为分数,因此这些数都是有理数. ② 到现在为止,我们学过的数(π 和无限不循环小数除外)都是有理数.有理数整数分数正整数0负整数正分数负分数有理数正有理数负有理数0正整数正分数负整数负分数 有理数的分类必须做到不重不漏,千万不要忘记 0,0是整数,但0既不是正数,也不是负数. 但是要注意一点:
相关资料
更多









