2023年山东省青岛市中考二模数学试题

2023年山东省青岛市中考数学二模试题（解答卷）

数学试题

（考试时间：120分钟     满分：120分）

说明：

1．本试题分第Ⅰ卷和第Ⅱ卷两部分，共25题．第Ⅰ卷为选择题，共8小题，24分；

第Ⅱ卷为填空题，作图题、解答题，共17小题，96分．

2．所有题目均在答题卡上作答，在试题上作答无效．

第Ⅰ卷（共24分）

一、选择题（本大题共8小题，每小题3分，共24分）

1. 我国“天问一号”探测器在火星成功着陆．火星具有和地球相近的环境，

与地球最近时候的距离约55000000km．将数字55000000用科学记数法表示为（　　）

A．0.55×108 B．5.5×107 C．5.5×106 D．55×106

解：将55000000用科学记数法表示为5.5×107．

故选：B．

2.下列三星堆文物图案中，既是中心对称图形又是轴对称图形的是（    ）

A． B． C． D．

解：  A选项中的图形既不是轴对称图形，也不是中心对称图形，不符合题意；

B选项中的图形是轴对称图形，是中心对称图形，选项符合题意；

C选项中的图形既不是轴对称图形，也不是中心对称图形，选项不符合题意；

D选项中的图形是轴对称图形，不是中心对称图形，选项不符合题意；

故选：B．

3. 下列各式计算正确的是（　　）

A． B． C． D．

解：A，，该选项计算错误，不合题意；

B，，该选项计算正确，符合题意；

C，，该选项计算错误，不合题意；

D，，该选项计算错误，不合题意；

故选B

4. 如图所示的几何体，其俯视图是（    ）

A． B． C． D．

解：由图形可知，这个几何体的俯视图为

故选A．

5.在抗击新型冠状病毒肺炎疫情中，某社区志愿者小分队10名队员年龄统计如下表：

则这10名队员年龄的中位数、众数分别是（    ）

A．20岁，35岁 B．26岁，22岁 C．22岁，26岁 D．30岁，30岁

解：在10名队员的年龄数据中，

排序后第5和第6个数据分别是22岁和30岁，

因而中位数是＝26岁，

这10名队员的年龄数据里，22岁出现了3次，次数最多，因而众数是22岁；

故选：B．

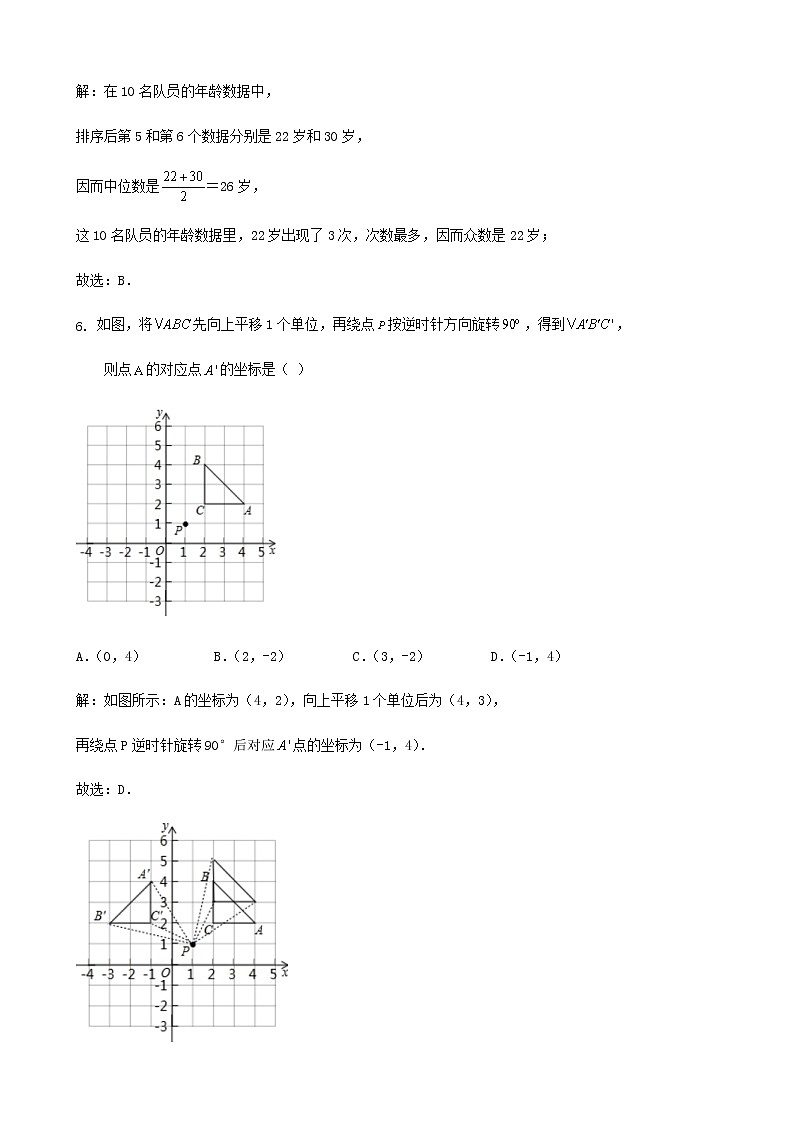
6. 如图，将先向上平移1个单位，再绕点按逆时针方向旋转，得到，

则点的对应点的坐标是（ ）

A．（0，4） B．（2，-2） C．（3，-2） D．（-1，4）

解：如图所示：A的坐标为（4，2），向上平移1个单位后为（4，3），

再绕点P逆时针旋转90°后对应点的坐标为（-1，4）．

故选：D．

7 如图，点，，均在上，若，则的度数是（      ）

A．  B． C． D．

解：∵，

∴，

∵，

∴，

故选C．

8. 已知反比例函数 y＝的图象如图所示，

则二次函数 y =ax 2－2x和一次函数 y＝bx+a 在同一平面直角坐标系中的图象可能是（       ）

A． B． C． D．

解：∵当x=0时，y=ax2-2x=0，即抛物线y=ax2-2x经过原点，故A错误；

∵反比例函数y=的图象在第一、三象限，

∴ab＞0，即a、b同号，

当a＜0时，抛物线y=ax2-2x的对称轴x=＜0，对称轴在y轴左边，故D错误；

当a＞0时，b＞0，直线y=bx+a经过第一、二、三象限，故B错误；

C正确．

故选C．

第Ⅱ卷（共96分）

二、填空题（本大题共6小题，每小题3分，共18分）

9．计算：_______．

解 ：∵，则，

∴．

故答案为：．

10.为调查落实“双减”政策效果，某班级随机调查了10名学生一周平均每天的睡眠时间，

统计结果如下表，则这些被调查学生的平均睡眠时间为__________小时．

解：这10名学生每天的平均睡眠时间是=9.3(小时)；

故答案为：9.3．

11.在卡塔尔世界杯上，来自中国制造的主体育场馆“大金碗”——卢塞尔体育场（图①），

融合了许多黑科技，球场顶棚采用环保膜材料，既可以为观众提供遮阳，

又能够给球场草地带来阳光．膜的材料结构是由许多正六边形交织而成的，

正六边形（图②）中，为______°．

解：∵六边形是正六边形，

∴每个内角均相等，

∴，

故答案为：120．

12. 《孙子算经》是中国古代最重要的数学著作，约成书于四、五世纪，其中记载：

“今有木，不知长短．引绳度之，余绳五尺五寸，屈绳量之，不足一尺，木长几何？”译文：

“用一根绳子去量一根长木，绳子还剩余尺，将绳子对折再量长木，长木还剩余1尺，问木长多少尺？”设绳子长x尺，木长y尺，可列方程组为___________．

解：根据题意可直接列出方程组：，

故答案为：．

13. 如图，正方形内接于，，分别与相切于点和点，

的延长线与的延长线交于点．已知，则图中阴影部分的面积为___________．

解：连接AC，OD，
 

∵四边形BCD是正方形，
∴∠B=90°，
∴AC是⊙O的直径，∠AOD=90°，
∵PA，PD分别与⊙O相切于点A和点D，
∴∠PAO=∠PDO=90°，
∴四边形AODP是矩形，
∵OA=OD，
∴矩形AODP是正方形，
∴∠P=90°，AP=AO，AC∥PE，
∴∠E=∠ACB=45°，
∴△CDE是等腰直角三角形，
∵AB=2，
∴AC=2AO=2，DE=CD=2，
∴AP=PD=AO=，
∴PE=3，

∴图中阴影部分的面积

故答案为：5-π．

14.正方形中，，为的中点，将沿折叠得到，于，

则______．

解：如图，过点F作MN BC，交AB于M，交CD于N，

四边形ABCD是正方形

∠B = ∠C = 90°

MN BC

∠AMF = ∠B = 90°，∠DNF=∠C= 90°

∠EMF = ∠DNF = 90°

由折叠得：AD= DF = 2， AE = EF，∠A = ∠EFD= 90°,

∠EFM + ∠DFN= ∠DFN+ ∠NDF= 90°

∠EFM=∠NDF

△EMF∽△FND

正方形ABCD中， AB = 2，E为AB的中点

AE= BE = EF = 1

设FH = BM=x，则EM= 1 – x，FN = 2EM = 2 (1 - x)= 2 – 2x

FM = 2 - FN = 2 -(2 -2 x)= 2 x

在Rt△EMF中，由勾股定理得：

EF2= EM2+ FM2

12=(1-x) 2 +(2x) 2

解得：x1=0，x2 =

FH=

故答案为：．

三、作图题（本大题满分4分）

15. 已知：如图，∠ABC，射线BC上一点D，

求作：等腰△PBD，使线段BD为等腰△PBD的底边，点P在∠ABC内部，且点P到∠ABC两边的距离相等．（不写作法，保留作图痕迹）

解：∵点P在∠ABC的平分线上，

∴点P到∠ABC两边的距离相等（角平分线上的点到角的两边距离相等），

∵点P在线段BD的垂直平分线上，

∴PB=PD（线段的垂直平分线上的点到线段的两个端点的距离相等），

如图所示：

四、解答题（本大题共10小题，共74分）

16 （1）化简：

解：原式=，

，

，

，

（2）解不等式组，并在数轴上画出该不等式组的解集

解：，

解不等式①得：，

解不等式②得：，

∴原不等式组的解集为，

在数轴上画出该不等式组的解集如下：

17.小颖和小亮都想去观看“垃圾分类”宣传演出，但只有一张入场券，于是他们设计了一个“配紫色”游戏：A，B是两个可以自由转动的转盘，每个转盘都被分成面积相等的几个扇形．同时转动两个转盘，如果其中一个转盘转出了红色，另一个转盘转出了蓝色，那么可以配成紫色．若配成紫色，则小颖去观看，否则小亮去观看．这个游戏对双方公平吗？请说明理由．

解：这个游戏公平，理由如下：

用列表法表示所有可能出现的结果如下：

共有6种可能出现的结果，其中配成紫色的有3种，配不成紫色的有3种，

∴P（小颖），

P（小亮），

因此游戏是公平．

18.某电信公司有甲、乙两种手机收费业务．

甲种业务规定月租费10元，每通话1 min收费0.3元；

乙种业务不收月租费，但每通话1 min收费0.4元.

(1)    你认为何时选择甲种业务对顾客更合算？  

(2)何时选择乙种业务对顾客更合算？

解：（1）设通话时长为x min，甲种业务收费y甲 ， 乙种业务收费y乙 ，

则y甲 ＝10＋0.3x，  y乙＝0.4x

当甲乙两种业务收费一样时，即y甲=y乙，得10+0.3x=0.4x，解得x=100；

当甲乙两种业务消费额不一样时，

①由y1>y2，得10+0.3x>0.4x，解得x<100；  此时选择乙种业务比较合算.

②由y1<y2，得10+0.3x<0.4x，解得x>100.   此时选择甲种业务比较合算.

19. 为助力苏州市双碳目标实现，充分挖掘学校光伏发电资源，学校屋顶安装了太阳能电板.

图①是太阳能电板的实物图，其截面示意图如图②，为太阳能电板，

其一端固定在水平面上且夹角，另一端与支撑钢架相连，

钢架底座和水平面垂直，且. 若，，求的长.

（参考数据：，结果精确到. ）

解：如图所示，过点B作于F，过点C作于E，则四边形是矩形，

∴，，，

∵，

∴，

∴，

∴，

设，

则，，

在中，，

∴，

解得，

∴，

∴，

∴的长约为．

20. 受疫情影响，开展线上教学活动．为了解学生上网课使用的设备类型，

某校从“电脑、手机、电视、其它”四种类型的设备对学生进行了一次抽样调查，

调查结果显示，每个学生只选择了以上四种设备类型中的一种，

现将调查的结果绘制成如图两幅不完整的统计图，请你根据图中提供的信息．解答下列问题：

(1)抽取的总人数是______，在扇形统计图中，“手机”所对应的扇形的圆心角的度数为______；

(2)补全条形统计图；

(3)在上网课时，老师在A、B、C、D四位同学中随机抽取一名学生回答问题．

请用列表法或画树状图的方法求两次都抽取到同一名学生回答问题的概率．

解：（1）抽取的总人数是：40÷40%=100（人），

手机的人数是：100-40-20-10=30（人），

在扇形统计图中，“手机”所对应的扇形的圆心角的度数为360°×=108°，

故答案为：100，108°；

(2)补全统计图如下：

；

(3)根据题意画树状图如下：

共有16种等情况数，其中两次都抽取到同一名学生回答问题的有4种，

则两次都抽取到同一名学生回答问题的概率为．

21. 如图，在矩形ABCD中,点E在BE上，AE =AD，DF⊥AE，垂足为F. 求证：DF=AB

证明:在矩形ABCD中，

AD//BC，∠B=90°，

∴∠1=∠2，

又∵DF⊥AE，

∴∠DFA=90°，

∴∠DFA=∠B，

又∵AD=EA

∴△ADF≌△EAB

∴DF=AB

22．如图，一次函数图象与反比例函数图象相交于，两点．

(1)求，的值；

(2)根据图象直接写出满足的的取值范围．

解：（1）点在一次函数与反比例函数图象上，

，

解得，

∴的值为3，的值为3．

（2）由（1）可知，反比例函数解析式为，

将代入，得，

∴，

∴由图象知，的取值范围为或．

23．如图，显示器的宽为22厘米，支架长14厘米，当支架与显示器的夹角，

支架与桌面的夹角，测得长为2厘米，求显示器顶端到桌面的高度的长

（，，）

解：如图，作延长线于点F，再延长DF、CB交于点G．

由题意可知．

∵，，

∴，

∴．

在中，．

∵，

∴．

在中，．

故显示器顶端到桌面的高度AD的长为25cm．

24. 某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种毛绒玩具．

据了解，只“冰墩墩”和只“雪容融”的进价共计元；

只“冰墩墩”和只“雪容融”的进价共计元．

(1)求“冰墩墩”和“雪容融”两种毛绒玩具每只进价分别是多少元．

(2)该专卖店计划恰好用元购进“冰墩墩”和“雪容融”两种毛绒玩具（两种均购买），

求专卖店共有几种采购方案．

(3)    若“冰墩墩”和“雪容融”两种毛绒玩具每只的售价分别是元，元，

则在（2）的条件下，请选出利润最大的采购方案，并求出最大利润．

解：（1）设“冰墩墩”毛绒玩具每只进价为元，“雪容融”毛绒玩具每只进价为元，

由题意得，，解方程组得，，

∴“冰墩墩”毛绒玩具每只进价为元，“雪容融”毛绒玩具每只进价为元．

（2）解：设购进“冰墩墩”毛绒玩具只，购进“雪容融”毛绒玩具只，

由题意得，，

整理得，，

∵、为正整数，

∴或或，

∴专卖店共有种采购方案．

（3）解：当，时，利润为：（元）；

当，时，利润为：（元）；

当，时，利润为：（元）；

∵，

∴利润最大的采购方案为购进“冰墩墩”毛绒玩具只，

购进“雪容融”毛绒玩具只，最大利润为元．

25. 如图1，已知和均为等腰直角三角形，点D、E分别在线段上，．

(1)    观察猜想：如图2，将绕点A逆时针旋转，连接，的延长线交于点F．

当的延长线恰好经过点E时，点E与点F重合，此时，

①的值为 　 　；

②的度数为 　 　度；

(2)类比探究：如图3，继续旋转，点F与点E不重合时，上述结论是否仍然成立，请说明理由．

(3)拓展延伸：若，，当所在的直线垂直于时，

请直接写出线段的长．

解：（1）如图所示，设与交于O，

∵和都是等腰直角三角形，，

∴，

∴，，，即，

∴，

∴，

∴，，

∵，

∴，

由于点E与点F重合，

∴，

故答案为：，45；

（2）解：设与交于O，

∵和都是等腰直角三角形，，

∴，

∴，，，即，

∴，

∴，

∴，，

∵，

∴；

（3）解：如图3-1所示，当于O时，

∵和都是等腰直角三角形，，，

∴同（1）可得，

∵，

∴，

∴，

∴，

同理可证，

∴，

∴；

如图3-2所示，当时，延长交于O．

同理可得，，，

∴；

综上所述，的长为或．