数学（温州卷）-学易金卷：2023年中考第三次模拟考试卷

2023年中考数学第三次模拟考试卷 （温州卷）

数  学

（考试时间：120分钟  试卷满分：150分）

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷

一、选择题（每小题4分，共40分．在每小题给出的四个选项中，只有一项符合题目要求

1．下列各实数中最小的是（　　）

A．|﹣2| B．0 C．﹣ D．﹣

2．2020年12月4日，中国量子计算原型机“九章”问世，当求解5000万个样本的高斯玻璃取样时，“九章”只需要200秒．其中数据5000用科学记数法表示为（　　）

A．0.5×103 B．0.5×104 C．5×103 D．5×104

3．下列几何体中的主视图为三角形的是（　　）

A．B． C．D．

4．把一枚均匀的骰子抛掷一次，朝上面的点数为6的概率是（　　）

A．0 B． C． D．1

5．将三角板（含30°，60°角）和直尺按如图所示的位置摆放，依次交于点F，D，E，且CD＝CE，那么∠BFA的度数为（　　）

A．120° B．135° C．140° D．150°

6．某校为了解学生在校一周体育锻炼时间，随机调查了35名学生，调查结果列表如下：

则这35名学生在校一周体育锻炼时间的众数为（　　）

A．6h B．5h C．7h D．8h

7．如图，四边形ABCD内接于⊙O，∠BAD＝90°，BC＝2，CD＝3，则⊙O的直径长为（　　）

A． B． C． D．

8．已知二次函数y＝﹣x2+2x+c，当﹣1≤x≤2时，函数的最大值与最小值的差为（　　）

A．1 B．2 C．3 D．4

9．如图，一只正方体箱子沿着斜面CG向上运动，∠C＝α，箱高AB＝1米，当BC＝2米时，点A离地面CE的距离是（　　）米．

A． B．

C．cosα+2sinα D．2cosα+sinα

10．如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH．连结EB，EG，延长EG交CD于点M，若∠BEM＝90°，则BE：EM的值为（　　）

A．1：2 B．3：4 C．5：6 D．5：12

第Ⅱ卷

二、填空题（本题有6小题，每小题5分，共30分）

11．分解因式：4m﹣2m2＝　          　．

12．小明数学的平时成绩，期中考试成绩，期末考试成绩分别是：90分，80分，90分．学校按平时成绩：期中考试成绩：期末考试成绩＝3：3：4进行总评，那么小明本学期数学总评分应为 　     　分．

13．若圆的半径为3cm，圆心角为60°，则这个圆心角所对的弧长为 　   　cm．

14．不等式组的解集为 　        　．

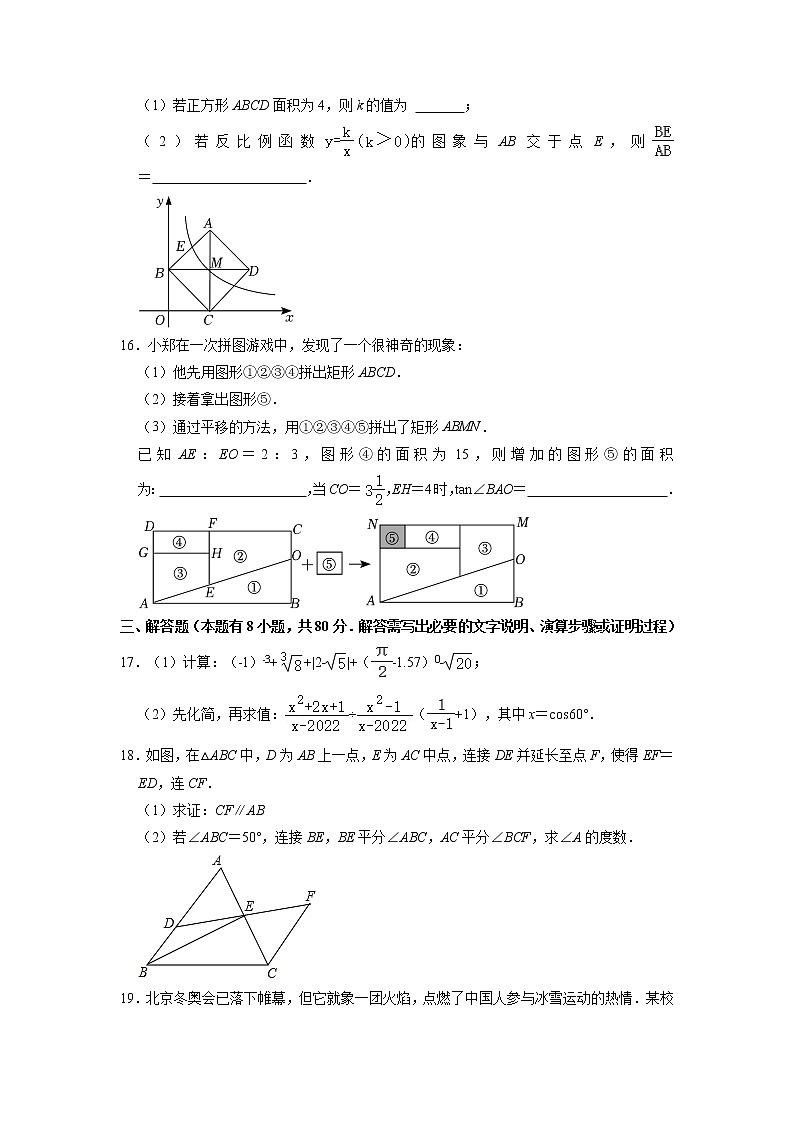
15．如图，正方形ABCD的顶点C，B分别在x，y轴的正半轴上，对角线AC，BD的交点M在第一象限，反比例函数的图象经过M点，已知AC⊥x轴．

（1）若正方形ABCD面积为4，则k的值为 　   　；

（2）若反比例函数的图象与AB交于点E，则＝　                  　．

16．小郑在一次拼图游戏中，发现了一个很神奇的现象：

（1）他先用图形①②③④拼出矩形ABCD．

（2）接着拿出图形⑤．

（3）通过平移的方法，用①②③④⑤拼出了矩形ABMN．

已知AE：EO＝2：3，图形④的面积为15，则增加的图形⑤的面积为：　                 　，当CO＝，EH＝4时，tan∠BAO＝　                　．

三、解答题（本题有8小题，共80分．解答需写出必要的文字说明、演算步骤或证明过程）

17．（1）计算：（﹣1）﹣3++|2﹣|+（﹣1.57）0﹣；

（2）先化简，再求值：÷﹣（+1），其中x＝cos60°．

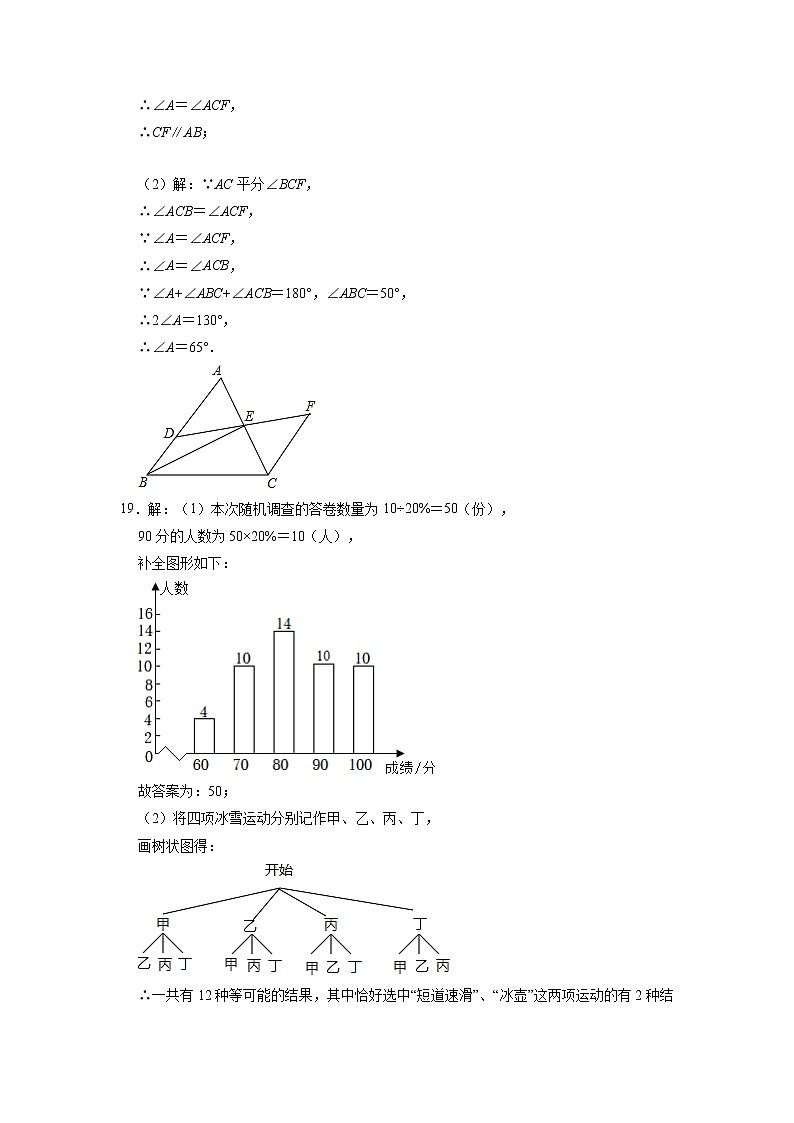
18．如图，在△ABC中，D为AB上一点，E为AC中点，连接DE并延长至点F，使得EF＝ED，连CF．

（1）求证：CF∥AB

（2）若∠ABC＝50°，连接BE，BE平分∠ABC，AC平分∠BCF，求∠A的度数．

19．北京冬奥会已落下帷幕，但它就象一团火焰，点燃了中国人参与冰雪运动的热情．某校为了解学生对冰雪运动相关知识的知晓情况，通过发放问卷进行测评．所有问卷全部收回，从中随机抽取若干份答卷，并统计成绩将结果绘制成如下所示的统计图（均不完整）．

请答下列问题：

（1）本次随机抽取了 　     　份答卷，并补全条形统计图；

（2）本班计划在“短道速滑”、“花样滑冰”、“单板滑雪”、“冰壶”四项冰雪运动中任选两项作为板报素材，求恰好选中“短道速滑”、“冰壶”这两项运动的概率.

20．如图，在8×6的方格纸中，△ABC的顶点均在格点上，请按下列要求完成作图．

（1）在图1中，将△ABC绕C点顺时针方向旋转90°，得到△A1B1C．

（2）在图2中，在AC所在直线的左侧画∠AEC，使得∠AEC＝∠B．

21．如图，矩形ABCD中，点E为边AB上一点，将△ADE沿DE折叠，使点A的对应点F恰好落在BC边上，连接AF交DE于点G，连接BG．

（1）求证：△GBF∽△DAF．

（2）若BF•AD＝15，cos∠BGF＝，求矩形ABCD的面积．

22．已知抛物线y＝ax2﹣4ax﹣6（a≠0）经过点（﹣1，﹣1）．

（1）求抛物线的函数表达式和顶点坐标；

（2）直线l交抛物线于点A（4，m），B（n，6），若点P在抛物线上且在直线l下方（不与点A，B重合），分别求出点P横坐标与纵坐标的取值范围．

23．某商店购进A，B两种商品共140件进行销售．已知采购A商品10件与B商品20件共170元，采购A商品20件与B商品30件共280元．

（1）求A，B商品每件进价分别是多少元？

（2）若该商店出售A，B两种商品时，先都以标价10元出售，售出一部分后再降价促销，都以标价的8折售完所有剩余商品．其中以10元售出的商品件数比购进A种商品件数少20件，该商店此次降价前后销售A，B两种商品共获利不少于360元，求商店至少购进A商品多少件？

（3）若采购这140件商品的费用不低于720元，不高于740元．然后将A商品每件加价2a元销售，B商品每件加价3a元销售，140件商品全部售出的最大利润为768元，请直接写出a的值．

24．如图1，△ABC中，∠ACB＝90°，AC＝8，BC＝6，延长BC至D，使CD＝CB，E为AC边上一点，连结DE并延长交AB于点F．作△BEF的外接圆⊙O，EH为⊙O的直径，射线AC交⊙O于点G，连结GH．

（1）求证：∠AEF＝∠CEB．

（2）①如图2，当DF⊥AB时，求GH的长及tan∠EHG的值．

②如图3，随着E点在CA边上从下向上移动，tan∠EHG的值是否发生变化，若不变，请你求出tan∠EHG的值，若变化，求出tan∠EHG的范围．

（3）若要使圆心O落在△ABC的内部（不包括边上），求CE的长度范围．