（统考版）2023高考数学二轮专题复习 第三篇 关键能力为重（研重点 保大分）专题三 立体几何 第3讲　空间向量与立体几何课件

这是一份（统考版）2023高考数学二轮专题复习 第三篇 关键能力为重（研重点 保大分）专题三 立体几何 第3讲　空间向量与立体几何课件，共48页。PPT课件主要包含了考点一，考点二，考点三，ka2，kb2，kc2，ka3，kb3，kc3，ka4等内容，欢迎下载使用。

考点一　向量法证明平行与垂直
考点一　向量法证明平行与垂直——建系，找点，写向量；平行，垂直，找关系设直线l，m的方向向量分别为a＝(a1，b1，c1)，b＝(a2，b2，c2)．平面α，β的法向量分别为u＝(a3，b3，c3)，v＝(a4，b4，c4)．(1)l∥m⇔a∥b⇔a＝kb⇔a1＝______，b1＝______，c1＝______；(2)l⊥m⇔a⊥b⇔a·b＝______⇔a1a2＋b1b2＋c1c2＝______；(3)l∥α⇔a⊥u⇔a·u＝______⇔a1a3＋b1b3＋c1c3＝______；(4)l⊥α⇔a∥u⇔a＝ku⇔a1＝______，b1＝______，c1＝_____；(5)α∥β⇔u∥v⇔u＝kv⇔a3＝______，b3＝______，c3＝______；(6)α⊥β⇔u⊥v⇔u·v＝0⇔a3a4＋b3b4＋c3c4＝______．
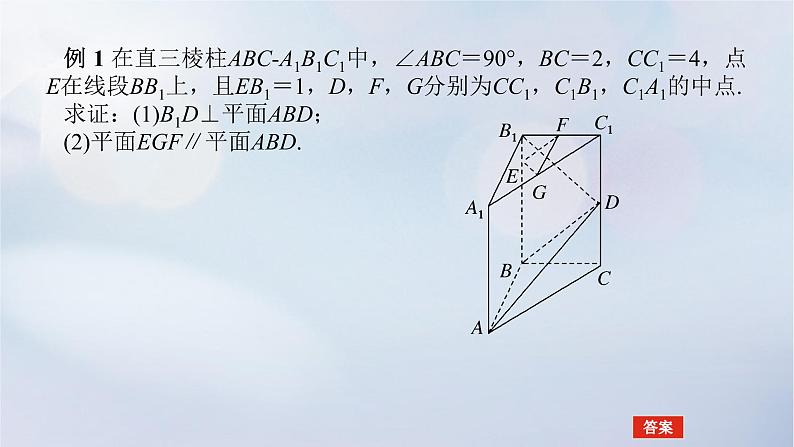
例 1 在直三棱柱ABC-A1B1C1中，∠ABC＝90°，BC＝2，CC1＝4，点E在线段BB1上，且EB1＝1，D，F，G分别为CC1，C1B1，C1A1的中点. 求证：(1)B1D⊥平面ABD；(2)平面EGF∥平面ABD.
归纳总结利用空间向量证明平行与垂直的步骤(1)建立空间直角坐标系，建系时，要尽可能地利用载体中的垂直关系；(2)建立空间图形与空间向量之间的关系，用空间向量表示出问题中所涉及的点、直线、平面中的要素；(3)通过空间向量的运算研究平行、垂直关系；(4)根据运算结果解释相关问题．
对点训练如图，在直三棱柱ADE-BCF中，平面ABFE和平面ABCD都是正方形且互相垂直，M为AB的中点，O为DF的中点，运用向量方法证明：(1)OM∥平面BCF；(2)平面MDF⊥平面EFCD.
考点二　向量法求空间角
例 2 [2022·全国乙卷理]如图，四面体ABCD中，AD⊥CD，AD＝CD，∠ADB＝∠BDC，E为AC的中点．(1)证明：平面BED⊥平面ACD；(2)设AB＝BD＝2，∠ACB＝60°，点F在BD上，当△AFC的面积最小时，求CF与平面ABD所成的角的正弦值．
归纳总结1．利用向量法求线面角的方法(1)分别求出斜线和它在平面内的射影的方向向量，转化为求两个方向向量的夹角(或其补角)；(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角(或钝角的补角)，取其余角就是斜线和平面所成的角．即线面角的正弦值等于斜线的方向向量与平面的法向量夹角余弦值的绝对值．2．利用向量法求二面角的方法(1)分别在二面角的两个半平面内找到一个与棱垂直且从垂足出发的两个向量，则这两个向量的夹角的大小就是二面角的大小；(2)通过平面的法向量来求：设二面角的两个半平面的法向量分别为n1和n2，则二面角的大小等于〈n1，n2〉(或π－〈n1，n2〉)．
提醒　求空间角注意：①两条异面直线所成的角α不一定是直线的方向向量的夹角β，即cs α＝|cs β|.②两平面的法向量的夹角不一定是所求的二面角，有可能为两法向量夹角的补角．③直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值，即注意函数名称的变化．
对点训练[2021·全国乙卷改编]如图，四棱锥P-ABCD的底面是矩形，PD⊥底面ABCD，PD＝DC＝1，M为BC的中点，且PB⊥AM.(1)求BC；(2)求二面角A-PM ­ B的正弦值；(3)求直线PB与CD所成的角；(4)求直线PB与平面PAM所成角的正弦值．
考点三　用向量法解决探索性问题
考点三　用向量法解决探索性问题——问题坐标化，探求方程解与空间向量有关的探究性问题主要有两类：一类是探究线面的位置关系；另一类是探究线面角或二面角满足特定要求时的存在性问题．处理原则：先建立空间直角坐标系，引入参数(有些是题中已给出)，设出关键点的坐标，然后探究这样的点是否存在，或参数是否满足要求，从而作出判断．
归纳总结利用空间向量巧解探索性问题(1)空间向量最适合于解决立体几何中的探索性问题，它无需进行复杂的作图、论证、推理，只需通过坐标运算进行判断．(2)解题时，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等．所以为使问题的解决更简单、有效，应善于运用这一方法解题．
[高考5个大题] 解题研诀窍(三) 立体几何问题重在“建”——建模、建系[思维流程——找突破口]
[技法指导——迁移搭桥]立体几何解答题建模、建系策略立体几何解答题的基本模式是论证推理与计算相结合，以某个几何体为依托，分步设问，逐层加深，解决这类题目的原则是建模、建系．建模——将问题转化为平行模型、垂直模型、平面化模型及角度、距离等的计算模型．建系——依托于题中的垂直条件，建立空间直角坐标系，利用空间向量求解．