精品解析： 2022年山东省聊城临清市中考三模数学试题（原卷版）

这是一份精品解析： 2022年山东省聊城临清市中考三模数学试题（原卷版），共8页。试卷主要包含了选择题，填空题，解答题，羊二，直金十九两；牛二等内容，欢迎下载使用。
1. 5的相反数是（ ）
A. 5B. C. D. 0.5
2. 下列图形中，是轴对称图形但不是中心对称图形的是（ ）
A. 正三角形B. 正方形C. 正六边形D. 圆
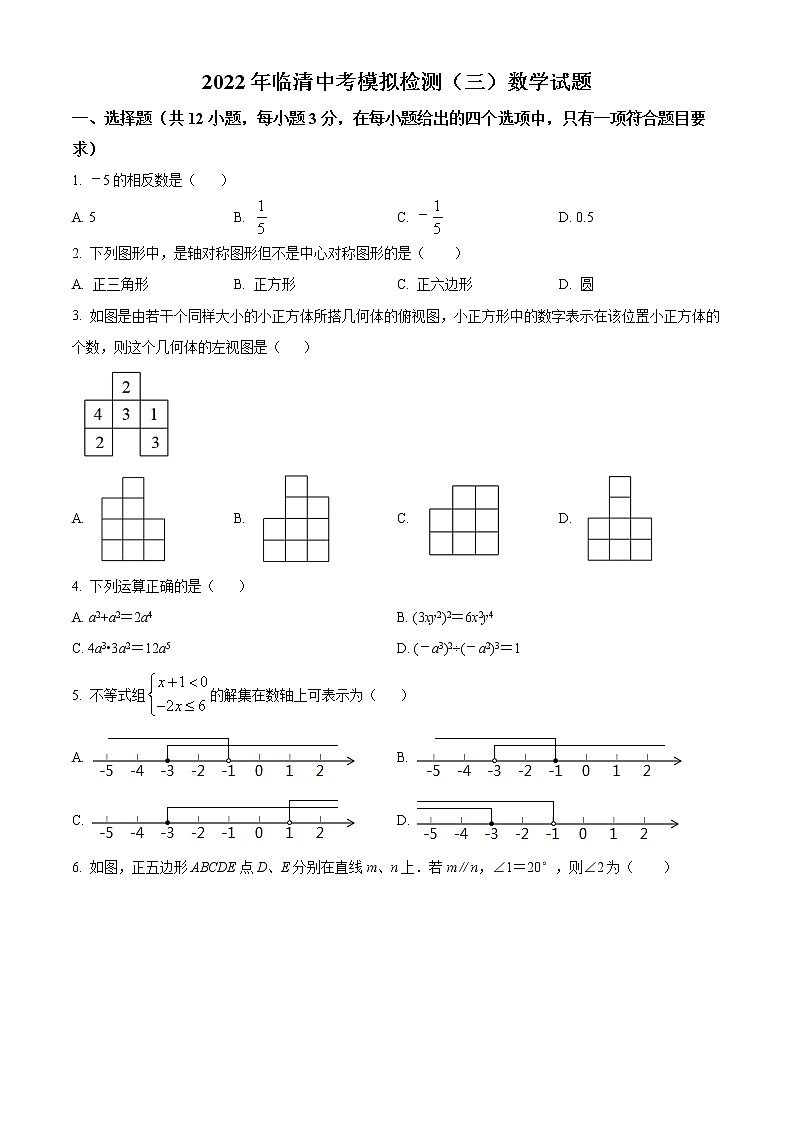
3. 如图是由若干个同样大小的小正方体所搭几何体的俯视图，小正方形中的数字表示在该位置小正方体的个数，则这个几何体的左视图是（ ）
A. B. C. D.
4. 下列运算正确的是（ ）
A. a2+a2＝2a4B. (3xy2)2＝6x2y4
C. 4a3•3a2＝12a5D. (a3)2÷(a2)3＝1
5. 不等式组的解集在数轴上可表示为（ ）
A. B.
C. D.
6. 如图，正五边形ABCDE点D、E分别在直线m、n上．若m∥n，∠1＝20°，则∠2为（ ）
A. 52°B. 60°C. 58°D. 56°
7. 一组数据：2，4，4，4，6，若去掉一个数据4，则下列统计量中发生变化的是（ ）
A. 众数B. 中位数C. 平均数D. 方差
8. 如图，Rt△ABC中，∠A＝30°，∠ABC＝90°．将Rt△ABC绕点B逆时针方向旋转得到．此时恰好点C在上，交AC于点E，则△ABE与△ABC的面积之比为（ ）
A. B. C. D.
9. 已知点A（x1，y1），B（x2，y2），C（x3，y3）都在反比例函数y（a是常数）的图象上，且y1＜y2＜0＜y3，则x1，x2，x3的大小关系为（ ）
A. x2＞x1＞x3B. x1＞x2＞x3C. x3＞x2＞x1D. x3＞x1＞x2
10. 已知：顶点，点C在x轴的正半轴上，按以下步骤作图：
①以点O为圆心，适当长为半径画弧，分别交于点M，交于点N．
②分别以点M，N为圆心，大于的长为半径画弧，两弧在内相交于点E．
③画射线，交于点，则点A的坐标为（ ）
A. B. C. D.
11. 如图，在以AB为直径的⊙O中，点C为圆上的一点，，弦CD⊥AB于点E，弦AF交CE于点H，交BC于点G．若点H是AG的中点，则∠CBF的度数为（ ）
A. 18°B. 20°C. 22.5°D. 30°
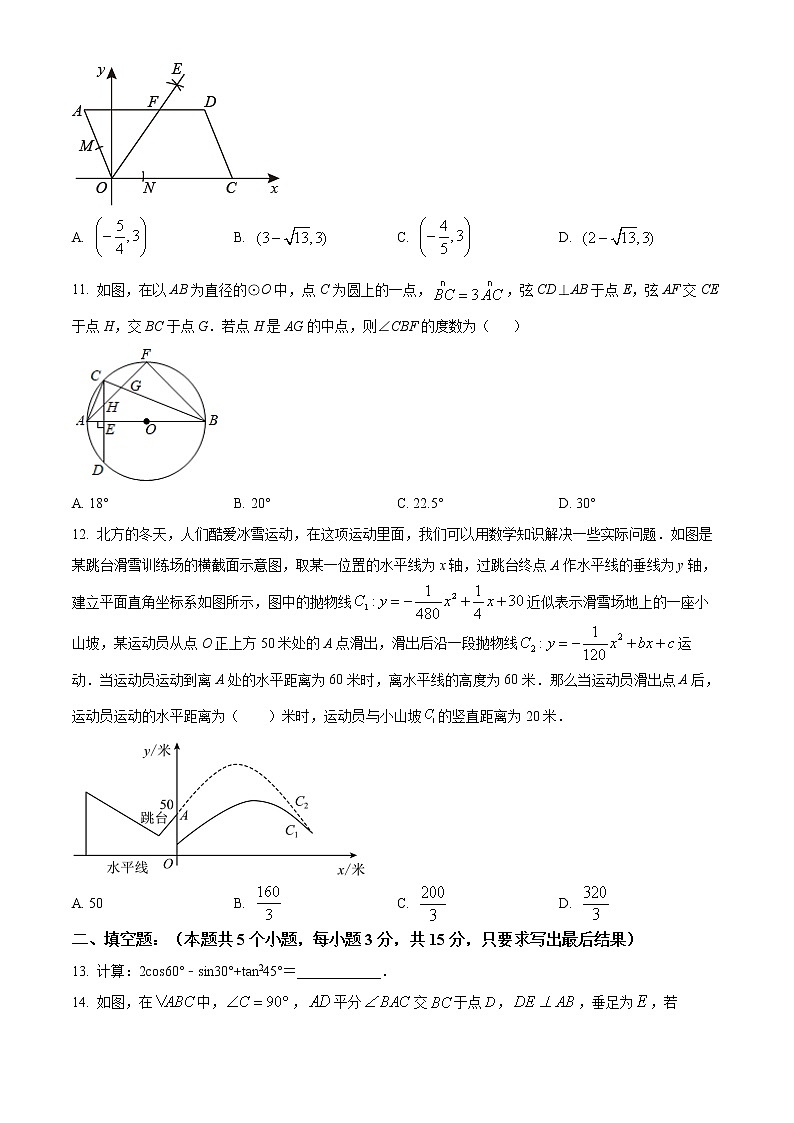
12. 北方的冬天，人们酷爱冰雪运动，在这项运动里面，我们可以用数学知识解决一些实际问题．如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点A作水平线的垂线为y轴，建立平面直角坐标系如图所示，图中的抛物线近似表示滑雪场地上的一座小山坡，某运动员从点O正上方50米处的A点滑出，滑出后沿一段抛物线运动．当运动员运动到离A处的水平距离为60米时，离水平线的高度为60米．那么当运动员滑出点A后，运动员运动的水平距离为（ ）米时，运动员与小山坡的竖直距离为20米．
A. 50B. C. D.
二、填空题：（本题共5个小题，每小题3分，共15分，只要求写出最后结果）
13. 计算：2cs60°﹣sin30°+tan245°＝____________．
14. 如图，在中，，平分交于点，，垂足为，若，，则的长为______．
15. 如图，随机闭合开关S1、S2、S3中的两个，则灯泡发光的概率为______．
16. 已知某几何体的三视图如图，其中主视图和左视图都是腰长为5，底边长为4的等腰三角形，则该几何体的侧面展开图的面积是____．（结果保留π）
17. 将二次函数y＝x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象，若直线y＝2x+b与这个新图象有3个公共点，则b的值为_____．
三、解答题：（本题共8小题，共69分．解答要写出必要的文字说明、证明过程或推演步骤．）
18. 先化简，然后从，0，1，3中选一个合适的数作为a的值代入求值．
19. 如图，已知△ABC中，D是AC的中点，过点D作DE⊥AC交BC于点E，过点A作AF∥BC交DE于点F，连接AE，CF．求证：四边形AECF是菱形．
20. 国家规定“中小学生每天在校体育活动时间不低于”．为此，某市就“每天在校体育活动时间”的问题随机调查了辖区内部分初中学生．根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：
组： 组：
组： 组：
请根据上述信息解答下列问题：
（1）本次调查的人数是____________人；
（2）请根据题中的信息补全频数分布直方图；
（3）组对应扇形的圆心角为__________；
（4）本次调查数据中位数落在__________组内；
（5）若该市辖区约有80000名初中学生，请估计其中达到国家规定体育活动时间的学生人数约有多少．
21. 我国传统数学名著《九章算术》记载：“今有牛五、羊二，直金十九两；牛二、羊五，直金十六两．问牛、羊各直金几何？”译文：“假设有5头牛、2只羊，值19两银子；2头牛、5只羊，值16两银子，问每头牛、每只羊分别值银子多少两？”
根据以上译文，提出以下两个问题：
（1）求每头牛、每只羊各值多少两银子？
（2）若某商人准备用19两银子买牛和羊（要求既有牛也有羊，且银两须全部用完），请问商人有几种购买方法？列出所有的可能．
22. 年月日，为我国载人空间站工程研制的长征五号运较火箭在海南文昌首飞成功．运载火箭从地面处发射、当火箭到达点时，地面处的雷达站测得米，仰角为．3秒后，火箭直线上升到达点处，此时地面处的雷达站测得处的仰角为．已知两处相距米，求火箭从到处的平均速度（结果精确到米，参考数据：）
23. 如图，正比例函数的图象与反比例函数（）的图象交于点，在中，，，点坐标为．
（1）求的值；
（2）求所在直线的解析式．
24. 如图，在Rt△ABC中，∠ACB＝90°，点E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝3，DE＝，求⊙O直径．
25. 如图，抛物线y= x2+bx+c的顶点D坐标为（1，4），且与轴相交于A，B两点点A在点B的左侧，与y轴相交于点C，点E在x轴上方且在对称轴左侧的抛物线上运动，点F在抛物线上并且和点E关于抛物线的对称轴对称，作矩形EFGH，其中点G，H都在x轴上．
（1）求抛物线解析式；
（2）设点F横坐标为m，
①用含有m代数式表示点E的横坐标为________（直接填空）；
②当矩形EFGH为正方形时，求点G的坐标；
③连接AD，当EG与AD垂直时，求点G的坐标；
（3）过顶点D作DM⊥x轴于点M，过点F作FP⊥AD于点P，直接写出△DFP与△DAM相似时，点F坐标．