2023年江苏省南京市秦淮区中考一模数学试题(含答案)

这是一份2023年江苏省南京市秦淮区中考一模数学试题(含答案)，共14页。试卷主要包含了计算的结果是________，不等式的解集是________等内容，欢迎下载使用。
2022—2023学年度第二学期第一阶段学业质量监测试卷
九年级数学
注意事项：
1．本试卷共8页，全卷满分120分，考试时间为120分钟．
2．答选择题必须用2B铅笔将答题卷上对应的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案，答非选择题必须用0.5毫米黑色墨水签字笔写在答题卷上的指定位置，在其他位置答题一律无效．
3．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．
一、选择题（本大题共6小题，每小题2分，共12分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卷相应位置上）
1．下列计算结果是正数的是（ ）
A． B． C． D．
2．64的立方根是（ ）
A．4 B． C．8 D．
3．某校用标准视力表检查全校学生的视力，并将全校学生的视力情况会制成如下的扇形统计图，则该校学生视力的中位数可能是（ ）

A．4.5 B．4.7 C．4.9 D．5.1
4．在三边长分别为a，b，的直角三角形中，下列数量关系不成立的是（ ）
A． B． C． D．
5．如图，用长为21m的栅栏围成一个面积为的矩形花圃ABCD．为方便进出，在边AB上留有一个宽1m的小门EF．设AD的长为xm，根据题意可得方程（ ）

A． B．
C． D．
6．如图，用7个棱长为1的正方体搭成一个几何体，沿着该几何体的表面从点M到点N的所有路径中，最短路径的长是（ ）

A．5 B． C． D．
二、填空题（本大题共10小题，每小题2分，共20分．请把答案填写在答题卷相应位置上）
7．“兔年报新春，金陵呈祥瑞”，2023年春节假日期间，南京市组织开展了丰富多彩的文化旅游活动，据初步统计测算，全市共接待游客6173600人次．用科学记数法表示6173600是________．
8．计算的结果是________．
9．不等式的解集是________．
10．计算的结果是________．
11．方程的解为________．
12．已知y是x的反比例函数，其部分对应值如下表：
x
…


1
2
…
y
…
a
b
m
n
…
若，则m________n．（填“”“”或“”）
13．如图是一个直角三角形纸片的一部分，测得，，，则原来的三角形纸片的面积是________．（结果精确到，参考数据：，，．）

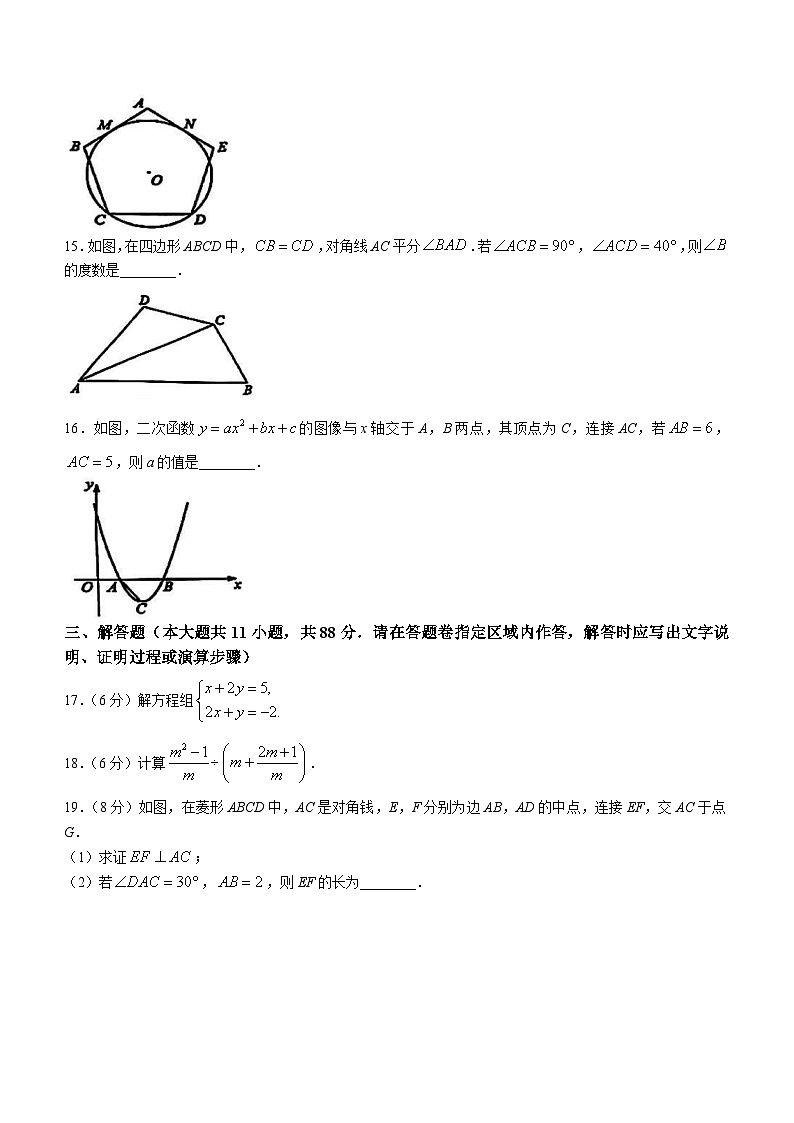
14．如图，与正五边形ABCDE的边AB，AE分别相切于点M，N，且经过点C，D．若的半径为2，则的长是________．（结果保留）

15．如图，在四边形ABCD中，，对角线AC平分．若，，则的度数是________．

16．如图，二次函数的图像与x轴交于A，B两点，其顶点为C，连接AC，若，，则a的值是________．

三、解答题（本大题共11小题，共88分．请在答题卷指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（6分）解方程组
18．（6分）计算．
19．（8分）如图，在菱形ABCD中，AC是对角钱，E，F分别为边AB，AD的中点，连接EF，交AC于点G．
（1）求证；
（2）若，，则EF的长为________．

20．（8分）2022年4月，教育部印发了新的《义务教育课程方案》，将劳动从原来的综合实践活动课程中独立出来．某校据此开展了“布艺”，“烹饪”，“家居美化”三门课．甲，乙，丙三名同学分别从中随机选择一门学习．
（1）求甲，乙选择的课相同的概率；
（2）甲，乙，丙选择的课均不相同的概率是________．
21．（8分）某商场销售一批衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，商场采取了降价措施．假设在一定范围内，衬衫的单价每降1元，商场平均每天可多售出2件．如果降价后商场销售这批衬衫每天盈利1250元，那么衬衫的单价降了多少元？
22．（8分）已知二次函数（a，m为然数，且）．
（1）求证：不论a，m为何值，该函数的图像与x轴总有两个公共点；
（2）将该函数的图像绕原点旋转180°，则所得到的图像对应的函数表达式为________．
23．（8分）截止到2022年12月，南京市已经开通了两类地铁钱——市区地铁线（1号，2号，3号，4号，10号）和市域地铁线（S1，S3，S6，S7，S8，S9）．经过长期统计，其日客运量有一定规律性．下图是某月连续13天两类地铁线日客运量的折线统计图．

（1）在这13天中，全市两类地铁线日客运量最多的一天总人数是________万人，最少的一天总人数是________万人；
（2）关于这13天的描述：
①对同一类地铁线而言，周六、周日的日客运量不超过工作日（周一到周五）的日客运量；
②市区地铁线平均日客运量是市域地铁线的6~7倍；
③市区地铁线日客运量比市域地铁线日客运量波动大．
其中正确的是________；（填序号）
（3）若该月20日市域地铁线客运量为21.8万人，试根据你发现的规律，估计当日市区地铁线客运量人数，并说明理由．
24．（8分）如图，在△ABC中，，直钱l与△ABC的外接圆相切于点B，D是l上一点，．
（1）求证：DC与△ABC的外接圆相切；
（2）若，则BC的长是________．

25．（8分）如图，已知线段a．求作△ABC，使，，且分别满足下列条件：
（1）．
（2）△ABC的周长等于a．
（要求：尺规作图，保留作图痕迹，写出必要的文字说明．）

26．（10分）慢车从甲地出发匀速驶往乙地，出发0.2h后快车也从甲地出发，匀速行驶，到达乙地后保持原速沿原路返回甲地．已知快车出发0.4h时第1次追上慢车．在整个行程中，慢车离甲地的距离（单位：km）与时间t（单位：h）之间的函数关系如图所示．

（1）在图中画出快车离甲地的距离（单位：km）与时间t之间的函数图像；
（2）若快车出发2.2h时与馋车第2次相遇．
①求快车从出发到返回甲地所用的时间；
②当两车第2次相遇的地点距离甲地240km时，s的值为________．
27．（10分）如图①~⑧是课本上的折纸活动．


【重温旧知】
上述活动，有的是为了折出特殊图形，如图①、③和⑧；有的是为了发现或证明定理，如图④和⑦；有的是计算角度，如图②；有的是计算长度，如图⑤和⑥．
（1）图③中的△ABC的形状是________，图④的活动发现了定理“________”（注：填写定理完整的表述），图⑤中的BF的长是________．
【新的发现】
（2）图⑧中，在第3次折后，点D落在点处，直接写出点的位置特点．
【换种折法】
（3）图⑧中，在第1次折后，再次折叠，如图⑨，使点A与点F重合，折痕为MN，点D落在点处，与CD交于点P．说明P为CD的三等分点．

【继续探索】
（4）如何折叠正方形纸片ABCD得到边AD的五等分点？请画出示意图，简述折叠过程，并说明理由．


2022—2023学年度第二学期第一阶段学业质量监测
九年级数学参考答案及评分标准
说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分．
一、选择题（每小题2分，共计12分）
题号
1
2
3
4
5
6
答案
B
A
B
C
B
A
二、填空题（每小题2分，共计20分）
7． 8．a 9． 10． 11．
12． 13．201 14． 15．65 16．
三、解答题（本大题共11小题，共计88分）
17．（本题6分）
方法一
解：由①，得．③ 1分
将③代入②，得． 3分
解这个一元一次方程，得． 4分
将代入③，得． 5分
所以原方程组的解是 6分
方法二
解：，得．③ 1分
，得． 3分
解这个一元一次方程，得． 4分
将代入①，得． 5分
所以原方程组的解是 6分
18．（本题6分）
解：原式 1分
2分
5分
． 6分
19．（本题8分）
（1）证法一
证明：∵四边形ABCD是菱形，
∴，． 2分
∴．
．
∴． 3分
∵E为边AB的中点，
∴．
同理．
∴． 4分
∵，，
∴． 6分

方法二
证明：连接BD交AC于点O．
∵四边形ABCD是菱形，
∴． 2分
∴．
∵E，F分别为边AB，AD的中点，
∴． 4分
∴，即． 6分

（2）1． 8分
20．（本题8分）
（1）解：甲，乙选择的课，可能出现的结果有9种，即（布艺，布艺），（布艺，烹饪），（布艺，家居美化），（烹饪，布艺），（烹饪，烹饪），（烹饪，家居美化），（家居美化，布艺），（家居美化，烹饪），（家居美化，家居美化），并且它们出现的可能性相同．其中甲，乙选择的课相同（记为事件A）的结果有3种，即（布艺，布艺），（烹饪，烹饪），（家居美化，家居美化），所以． 6分
（2）． 8分
21．（本题8分）
解：设衬衫的单价降了x元．
根据题意，得． 5分
整理，得．
解这个方程，得． 7分
答：衬衫的单价降了15元． 8分
22．（本题8分）
（1）方法一
证明：令，得方程． 1分
因为一元二次方程的根的判别式
． 3分
因为，所以． 4分
所以方程有两个不相等的实数根． 5分
所以不论a，m为何值，该函数的图像与x轴总有两个公共点． 6分
方法二
证明：令，得方程． 1分
因为，所以，． 3分
因为， 4分
所以方程有两个不相等的实数想． 5分
所以不论a，m为何值，该函数的图像与x轴总有两个公共点． 6分
方法三
证明：令，得方程． 1分
因为，所以原方程可化为． 3分
因为， 4分
所以方程有两个不相等的实数根． 5分
所以不论a，m为何值，该函数的图像与x轴总有两个公共点． 6分
（2）． 8分
（说明：也可写成）
23．（本题8分）
解：（1）262.8；165.4． 2分
（2）①③． 4分
（3）该月12日（周六）市区地铁线和市域地铁线客运量的差为（万人），
该月19日（周六）市区地铁线和市域地铁线客运量的差为（万人）．
由此可知，周六市区地铁线和市域地铁线客运量的差基本一致．
因为该月13日（周日）市区地铁线和市域地铁线客运量的差为（万人），
推测该月20日（周日）市区地铁线客运量为（万人）． 8分
（说明：根据周日比周六客运量小的规律，得到周日市区地铁线客运量小于171.5万人但不在140万人~145万人之间，得2分；根据周日市区和市域地铁线客运量的比例关系，得到周日市区地铁缆客运量为140万人~145万人之间，得4分）
24．（本题8分）
（1）证明：设AB中点为O，连接OC．
∵，
∴AB是△ABC的外接圆的直径． 1分
∴O为△ABC的外接圆的圆心．
∵直线l与相切于点B，
∴． 2分
∵，∴．
∵，∴．
∵，∴．
∴，即． 4分
又∵点C在上， 5分
∴DC与相切，即DC与△ABC的外接圆相切． 6分

（2）． 8分
25．（本题8分）
解：（1）如图①，△ABC即为所求． 4分
（2）作法不唯一，如图②、③、④中的△ABC均为所求． 8分

26．（本题10分）
解：（1）与t之间的函敷图像如图所示． 4分

（说明：A，B，C，D四个点，每个点正确得1分．）
（2）①方法一
设慢车速度为，快车速度为．
根据题意，得．
即． 5分
根据题意，得．
因为，所以点E的坐标为．
设CD的函数表达式为．
将代入，得．
即CD的函数表达式为． 6分
令，得． 7分
（h），即快车从出发到返回甲地所用的时间为3.8h． 8分
方法二
设慢车速度为，快车速度为．
根据题意，得．
即． 5分
设快车从第2次相遇到回到甲地需xh．
． 6分
结合，可得． 7分
（h），即快车从出发到返回甲地所用的时间为3.8h． 8分
②285． 10分
27．（本题10分）
解：（1）等腰三角形． 1分
直角三角形斜边上的中线等于斜边的一半． 2分
． 3分
（2）点在BG上，且是BG的中点． 5分
（说明：只写“是BG的中点”得满分，只写“点在BG上”得1分，只写“”得1分）
（3）设，，由题意，得，，．
∵△BMF为直角三角形，，∴．
∴．解得． 6分
∵，，
∴．
∴．∴．
∴．解得．
∴P为CD的三等分点． 7分

（4）方法一
如图①，P为CD的三等分点．折叠正方形纸片ABCD，使点B与点P重合，折痕为HG，点A落在点处，与AD交于点Q，则Q为AD的五等分点．
理由：设，在Rt△PCG中，根据勾股定理，易得．易证，可得．所以Q是AD的五等分点． 10分

方法二
如图②，E为BC的中点．折叠正方形纸片ABCD，使得折痕为AE，点B落在点处，再次折叠，使得折痕GH经过点且点D落在边AD上，则G为AD的五等分点．
理由：设，易证，且相似比为1：2，可得，
所以G是AD的五等分点． 10分
方法三
如图③，将正方形纸片ABCD对折3次并展开后，可得，再次折叠，使得折痕为DG并且点A落在MN上，落点记为，交EF于点K，则K为（AD）的五等分点．
理由：易证，所以K是（AD）的五等分点． 10分