







所属成套资源:浙教版数学七年级上学期课件PPT+练习全套
数学1.3 绝对值优质课ppt课件
展开
这是一份数学1.3 绝对值优质课ppt课件,文件包含浙教版数学七上13绝对值课件pptx、浙教版数学七上13绝对值练习docx等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
1.3绝对值一.选择题1.已知有理数,,且,,,则下列结论正确的是 A. B. C. D.2.已知与互为相反数,则的值为 A. B.0 C.1 D.23.下列各式正确的是 A. B. C. D.4. 的绝对值是 A. B.2020 C. D.5. ,则等于 A. B.1 C.0 D.二.填空题6.实数,在数学上的位置如图所示,则化简代数式的结果是 .7.设,则的最大值与最小值之和为 .8.如图,化简代数式的结果是 .9.若与互为相反数,则 .10.若与互为相反数,则 .三.解答题11.若,求的相反数. 12.已知实数,,满足:,.(1)求,,中的最小者的最大值;(2)求的最小值. 13.有理数、、的位置如图所示,化简式子:. 14.有理数、、在数轴上的位置如图:(1)判断正负,用“”或“”填空: 0, 0, 0.(2)化简:. 15.同学们都知道,表示4与的差的绝对值,实际上也可理解为4与两数在数轴上所对应的两点之间的距离;同理也可理解为与3两数在数轴上所对应的两点之间的距离.试探索:(1)求 ;(2)若,则 ;(3)请你找出所有符合条件的整数,使得. 16.(2018秋•灌云县月考)已知、在数轴上分别表示、.(1)对照数轴填写下表:6240、两点的距离2 0(2)若、两点间的距离记为,试问和、有何数量关系;(3)写出数轴上到和1的距离之和为2的所有整数;(4)若点表示的数为,代数式取最小值时,相应的的取值范围是 ,此时代数式的最小值是 .
参考答案一.选择题1.【解答】解:,,,,故正确,错误;,,,,,,故、错误.故选:.2.【解答】解:因为与互为相反数,所以,所以,,解得,,则,故选:.3.【解答】解:、,,,原式错误,故此选项不符合题意;、,,原式错误,故此选项不符合题意;、,,,原式正确,故此选项符合题意;、,,,原式错误,故此选项不符合题意.故选:.4.【解答】解:根据绝对值的概念可知:,故选:.5.【解答】解:,,,.故选:.二.填空题6.【解答】解:由数轴上各点的位置可知:,且..故答案为:.7.【解答】解:,当时,,最大值为5,最小值为4.5;当时,,最大值为5,最小值为3.5,最大值与最小值之和为8.5;故答案为:8.5.8.【解答】解:由有理数、、在数轴上的位置,可得,,,所以有,,,因此,故答案为:3.9.【解答】解:由题意得,,则,,解得,,,,故答案为:15.10.【解答】解:与互为相反数,,,,解得,,所以,.故答案为:1.三.解答题11.【解答】解:,,,解得,,,的相反数是.12.【解答】解:(1)不妨设是,,中的最小者,即,,由题设知,且,,于是,是一元二次方程的两实根,即,,,所以;又当,时,满足题意.故,,中最小者的最大值. (2)因为,所以,,为全小于0或二正一负.①当,,为全小于0,则由(1)知,,,中的最小者不大于,这与矛盾.②若,,为二正一负,设,,,则,当,时,满足题设条件且使得不等式等号成立.故的最小值为6.13.【解答】解:由数轴可得:,,,,故:.14.【解答】解:(1)由图可知,,,且,所以,,,;故答案为:,,; (2).15.【解答】解:(1)原式;(2),,或;(3)由题意可知:表示数到1和的距离之和,,或或0或1.故答案为(1)6;(2)7或;16.【解答】解:(1),,,故填:6,2,12;(2);(3)数轴上到和1的距离之和为2的所有整数为:,0,1;(4)在数轴上的几何意义是:表示有理数的点到及到2的距离之和,所以当时,它的最小值为3;故答案为:,3.
相关课件
这是一份数学七年级上册1.3 绝对值教学演示ppt课件,共20页。PPT课件主要包含了数轴的三要素,正方向,单位长度,绝对值的表示方法,绝对值,绝对值的代数意义,绝对值的性质,或-4,或-3,谁能逃离危险等内容,欢迎下载使用。
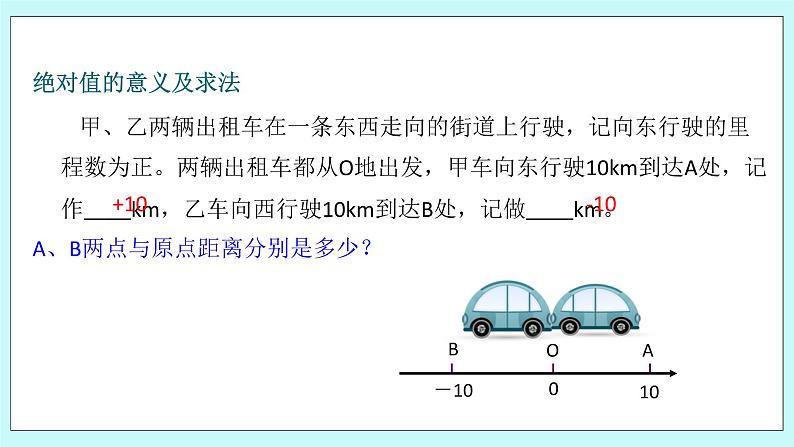
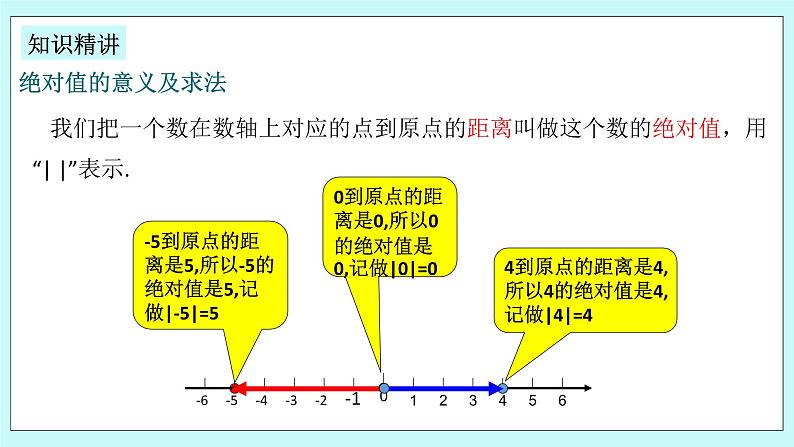
这是一份初中数学浙教版七年级上册第1章 有理数1.3 绝对值教学ppt课件,共10页。PPT课件主要包含了两只小狗呢,-3到原点的距离是3,+3到原点的距离是3等内容,欢迎下载使用。
这是一份初中数学浙教版七年级上册1.3 绝对值获奖课件ppt,文件包含浙教版数学七上13绝对值课件pptx、浙教版数学七上13绝对值练习docx等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。










