
【精品同步】数学小升初同步培优练习六年级下册第三单元 圆柱与圆锥(知识梳理+含答案)
展开
这是一份【精品同步】数学小升初同步培优练习六年级下册第三单元 圆柱与圆锥(知识梳理+含答案),共60页。试卷主要包含了1 圆柱的认识,4m,这根木料的体积是m³,12cm²,57米等内容,欢迎下载使用。
了解圆柱的特征,认识圆柱的底面及其直径和半径,圆柱的高、侧面及圆柱的展开图。
通过观察,认识圆柱并掌握它的特征,建立空间概念。
1、在日常生活中,人们把许多建筑设计成圆柱形,增加立体感、美感。如……
2、在生活中,人们也经常把生活物品设计成圆柱形,让其更加实用。如……
提问:(1)请问一下这一些物体都要哪一些相同的地方呢?
(2)这种类似的形状的物品有几个面呢?有什么特征?
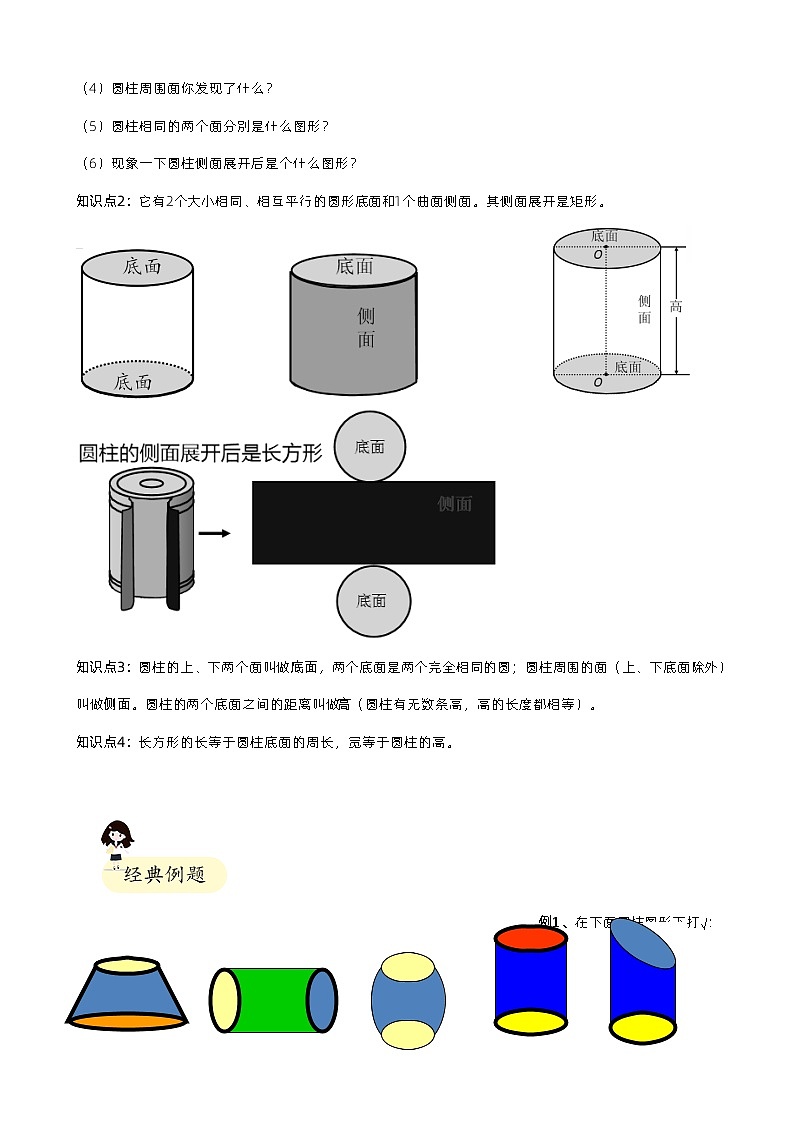
知识点1:类似上图物品叫做圆柱;圆柱:圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。
(3)圆柱一共有几个面,是那几个面?
(4)圆柱周围面你发现了什么?
(5)圆柱相同的两个面分别是什么图形?
(6)现象一下圆柱侧面展开后是个什么图形?
知识点2:它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。
知识点3:圆柱的上、下两个面叫做底面,两个底面是两个完全相同的圆;圆柱周围的面(上、下底面除外)叫做侧面。圆柱的两个底面之间的距离叫做高(圆柱有无数条高,高的长度都相等)。
知识点4:长方形的长等于圆柱底面的周长,宽等于圆柱的高。
例1、在下面圆柱图形下打√:
( )
( )
( )
( )
( )
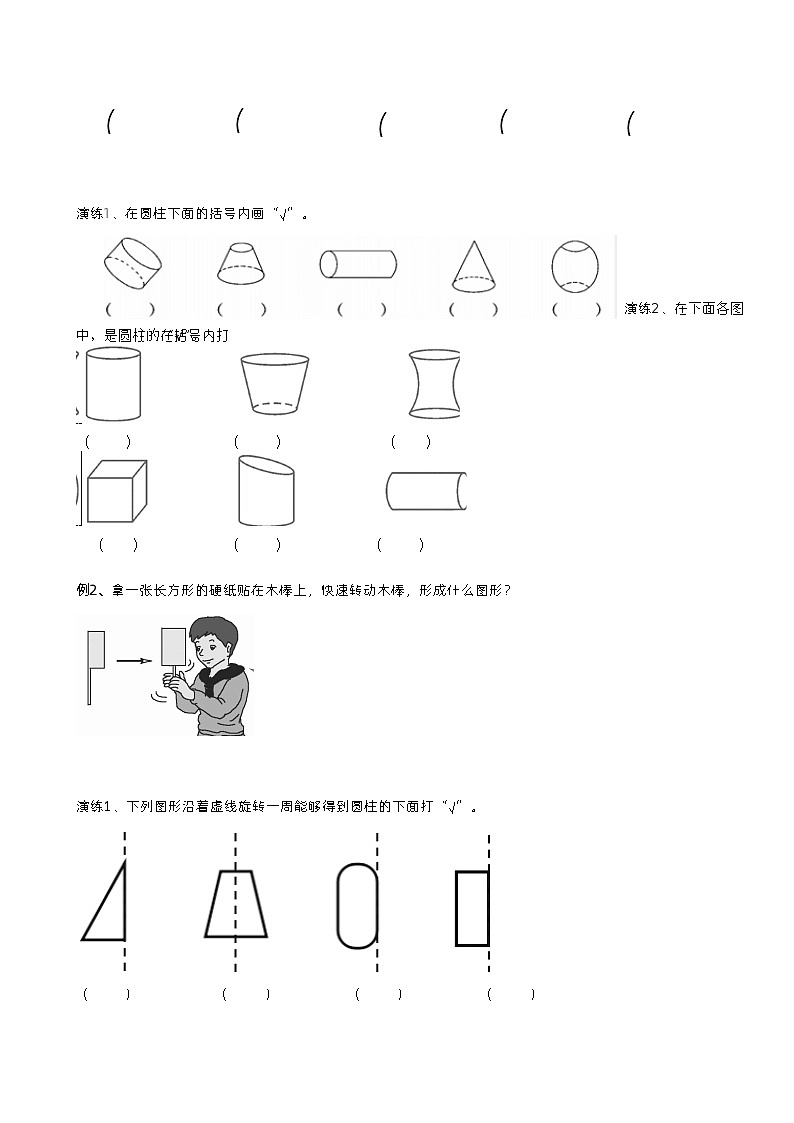
演练1、在圆柱下面的括号内画“√”。
演练2、在下面各图中,是圆柱的在括号内打“√”。
( ) ( ) ( )
( ) ( ) ( )
例2、拿一张长方形的硬纸贴在木棒上,快速转动木棒,形成什么图形?
演练1、下列图形沿着虚线旋转一周能够得到圆柱的下面打“√”。
( ) ( ) ( ) ( )
1、下图中是圆柱的请在括号内画“√”,不是的画“×”。
( ) ( ) ( ) ( )
2、指出下列圆柱的底面、侧面、高。
3、转动长方形ABCD,可以生成( )个圆柱。说说它们分别是以长方形的哪条边为轴旋转而成的,底面半径和高分别是多少。
A 2cm B
1cm
C D
4、将下面的纸板以一边为轴快速旋转一周,能形成底面直径4厘米,高4厘米的圆柱的是( )
2cm
4cm
4cm
4cm
A B
3.2 圆柱的表面积和体积
1、理解圆柱的表面积的意义。
2、探索并掌握圆柱的侧面积和表面积的计算方法,会正确地计算圆柱的侧面积和表面积。
3、探索并掌握圆柱的体积计算公式,会运用公式计算圆柱的体积,体会转化的思想方法。
1、口头回答下面的问题。
(1)一个圆形花池,直径是5m,周长是多少?
(2)长方形的面积怎样计算?
2、回顾一下上节课学习过的,圆柱的侧面展开是一个什么图形?
问题:1、圆柱的侧面积与展开后的长方形的面积有什么关系?
2、圆柱的侧面积与底面有什么关系?
知识点1:圆柱的侧面积=底面周长×高,;
知识点2:圆柱的表面积是指圆柱的侧面和两个底面的面积之和;圆柱的表面积=圆柱的侧面积+两个底面的面积,圆柱的侧面积=底面周长×高,。
观察下列图形,说一说下列图形的体积是如何计算的?
提问:
请你说一说如何计算长方体、正方体的体积?
(2)能不能将圆柱转化成我们学过的立体图形,计算出它的体积呢?
4、观察下面圆柱图形的变化,能得到什么结论呢?
我们发现把圆柱切开,再像这样拼起来,得到一个近似的长方体,把圆柱的底面分成许多相等的扇形,分成的扇形越多,拼成的立体图形就越接近于长方体。
知识点3:这个接近于长方体的体积就是圆柱的体积,故可以用长方体的体积计算方法计算圆柱的体积。
例1、填空题。
(1)用一张边长是5dm的正方形纸围成一个最大的空圆柱,圆柱的底面周长是( )dm,高是( )dm,侧面积是( )dm²。
(2)把一个底面积是6.28cm²的圆柱切成两个大小相等的圆柱,表面积增加了( )cm²。
(3)计算做一个圆柱形的烟筒要用多少铁皮,要计算圆柱的( )。
演练、填空题。
做一个没有盖的圆柱形玻璃鱼缸需要多少玻璃是求( );求压力机滚筒滚动一周压路的面积是求滚筒的( )。
(2)一个圆柱形铁皮水桶的底面半径是1.5dm,高是4dm,做10个这样的水桶至少需要( )dm²的铁皮。(得数保留整十数)
(3)一个圆柱体侧面积是1.05m²,高是0.7m,底面周长是( )m。
例2、计算下面圆柱的侧面积。
演练1、求下面圆柱的侧面积。
(1)底面周长是1.6m,高是0.7m。
底面半径是3.2dm,高是5dm。
演练2、一种圆形通风管的底面直径是8dm,长是50dm。制作15节这样的通风管至少需要多少平方米铁皮?
例3、计算下面各圆柱的表面积。
演练、如图是一个圆柱形铁皮油桶(油桶有盖),这个油桶的表面积是多少平方分米?
例4、一顶圆柱形厨师帽,高26cm,帽顶直径20cm,做这样一顶帽子需要用多少面料?(得数保留整十平方厘米)
演练1、一台压路机的前轮是圆柱形的,轮宽2m,直径1.2m。前轮转动一周,压路的面积是多少平方米?
演练2、一个圆柱形茶叶桶的侧面贴着商标纸,圆柱底面半径是5cm,高是20cm。这张商标纸的面积是多少?
例5、小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要多少彩纸?
演练1、油桶的外表面要刷上防锈油漆,每平方米需要用防锈油漆0.2kg,如图,漆这样一个油桶大约需要多少千克防锈油漆?(结果保留两位小数)
演练2、小宁把衣蛾圆柱形的易拉罐的侧面沿高剪开,得到如下图形,这个易拉罐的表面积是多少?
例6、填空题
(1)如图,把一个圆柱形沿半径分割成,若干等份,拼成一个近似的长方体,长方体的长等于圆柱的( ),长方体的宽等于圆柱的( ),长方体的底面积等于圆柱的( ),高等于圆柱的( )。
(2)一个圆柱的底面半径是2dm,高是1.5dm,它的体积是( )dm³。
(3)一根圆柱形木料的底面积是15dm²,高是2.4m,这根木料的体积是( )m³。
演练、填空题。
一个圆柱的底面半径是2cm,高是5cm,它的底面积是( )cm²,表面积是( )cm²,体积是( )cm³。
有一块正方体的石料,棱长是6dm,把这块石料加工成一个最大的圆柱,这个圆柱的体积是( )dm³。
如右图一瓶装满的果汁,小明喝了一些,把瓶盖拧紧后倒置放平,无果汁部分高5cm,内直径是6cm,小明喝了( )ml果汁。
例7、看图计算下面圆柱的体积。
例8、下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的)
演练1、小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量底面直径是8cm,高是15cm。
如果两人游玩期间要喝1L水,带这杯水够喝吗?
演练2、一个圆柱形粮囤,从里面量得底面半径是1.5m,高2m。如果每立方米玉米约重750kg,这个粮囤能
装多少吨玉米?
演练3、学校建了两个同样大小的圆柱形花坛,花坛的底面内直径为3m,高为0.8m。如果里面填土的高度
是0.5m,两个花坛中共需要填土多少立方米?
例9、一根圆柱形木料,底面积为75cm² ,长90cm。它的体积是多少?
演练1、一个圆柱形油桶的底面积是50dm²,高是12dm,桶内装油的高度是桶高的,桶内装油多少升?(桶的厚度不计)
例10、一个圆柱形玻璃容器,底面直径是8cm,里面装有一些水,把一个石块放入水中(完全浸没),水面上升了3cm(水未溢出)。这个石块的体积是多少立方厘米?
演练1、一个长方体玻璃容器,长和宽都是4dm,里面装了一些水,把一个底面半径是1dm,高是3dm的圆柱形铁块放入其中完全浸没,请问水面上升了多高?(结果保留两位小数)
例11、两个完全一样的圆柱能拼成一个高12cm的圆柱,但表面积减少25.12cm²。原来一个圆柱的体积是多少立方厘米?
演练1、将一根长1米圆柱体木条截成三段小圆柱体木条,表面积增加4平方分米,这根圆柱形木条原来的体积是多少立方分米?
演练2、一个圆柱体,底面直径是8厘米,高是10厘米,把它沿着直径垂直锯成两半,表面积增加了多少平方厘米?
演练3、一根底面积是31.4平方厘米的圆柱体,被切割后变成如图所示,请问它被切割后余下的体积是多少?
1、选一选,并填空。
做一个水桶需要多少铁皮 ( )
求圆柱形蓄水池的占地面积 ( )
压路机滚筒一周压路的面积 ( )
油漆大厅柱子的面积是多少 ( )
做一节通风管需多少铁皮 ( )
A、求圆柱的2个底面积与侧面积的和
B、求圆柱的1个底面积与侧面积的和
C、求圆柱的侧面积
D、求圆柱的底面积
2、一个圆柱的底面直径是8分米,高是3分米,它的侧面积是多少平方分米?
3、一个圆柱的底面周长是12.56厘米,高是4厘米,求它的表面积。
4、一个圆柱形蓄水池,底面周长是25.12米,高是4米,将这个蓄水池四周及底部抹上水泥。如果每平方米要用水泥20千克,一共要用多少千克水泥?
5、计算下面各圆柱的表面积和体积。
6、一个酸奶瓶,它的瓶身呈圆柱形(不包括瓶颈),底面半径4厘米,当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余部分高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?
7、一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10厘米,内直径是6厘米。小明喝了多少水?
8、一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸在这个容器的水中的铁块取出后,水面下降2cm,求这块铁块的体积。
9、把一块长31.4cm、宽20cm、高4cm的长方体钢坯熔铸成底面半径是4cm的圆柱,圆柱的高是多少厘米?
10、有一个底面周长为12.56cm的圆柱,从中间斜着截去一半,剩余部分的体积是多少立方厘米?
3.3 圆锥的认识和体积
认识圆锥,掌握它的各部分名称及特征。
认识圆锥的高,掌握测量圆锥的高的方法。
参与实验,从而推导出圆锥体积的计算公式,会运用圆锥的体积公式计算圆锥的体积。
培养初步的空间观念,经历圆锥体积公式的推导过程,体验观察、比较、分析、总结、归纳的学习方法。
1、观察下面图片,看这些物体的形状有什么共同特点?
上面这些物体的形状都是圆锥体,简称圆锥。
2、圆锥有哪些特征呢?
知识点1:圆锥的底面是一个圆,侧面是一个曲面,侧面展开图是一个扇形。
3、圆柱的高。
知识点2:从圆锥的顶点到底面圆心的距离是圆锥的高,圆锥的高只有1条。
圆柱与圆锥的区别。
我们已经会计算圆柱的体积,如何计算圆锥的体积呢?圆柱的底面是圆,圆锥的底面也是圆,圆锥的体积和圆柱的体积有没有关系呢?我们用同底同高的圆柱和圆锥倒水来探究他们的体积关系。
① ② ③
④ ⑤
在空圆锥容器里装满水,然后倒入空圆柱形的容器里,经试验,3次正好将空圆柱形容器装满。
依据上面的实验我们来推到一下圆锥的体积公式:
知识点3:如果用V表示圆锥的体积,S表示圆锥的底面积,h表示高,那么V=Sh;圆锥的体积=圆锥的底面积×高×。
例1、下面图形以左边线为轴快速旋转后会形成什么图形?连一连。
演练1、下面图形以左边线为轴快速旋转后会形成什么图形?连一连。
例2、填空题。
(1)从圆锥的( )到底面( )的距离叫做圆锥的高,圆锥有( )条高。
(2)如右图,以直角三角形的一条直角边为轴旋转一周,可得到一个( ),它的高是( )cm,2cm是它的( )。
(3)右图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子中,能到满( )杯。
(4)一个圆柱的体积是45cm³,与它等底等高的圆锥体积是( )cm³。
(5)等底等高的一个圆柱和一个圆锥的体积和是96cm³,圆柱的体积是( )cm³,圆锥的体积是( )cm³。
演练、填空题。
将底面半径为10cm,高是8cm的圆锥沿着高切开,得到的截面是一个( )三角形,这个三角形的底是( )cm,高是( )cm。
圆锥的底面半径是3cm,高是21cm,它的体积是( )cm³。
一个圆锥的高是4.5dm,体积是90dm³,它的底面面积是( )cm³。
一个圆锥的底面半径是1cm,体积是12.56cm³,这个圆锥的高是( )cm。
例3、一个圆形纸片,它的 半径是8cm,把它剪成4个大小完全相等的扇形,分别做成最大的圆锥,每个圆锥的底面周长是多少厘米?
演练1、一个圆锥形谷堆的底面周长是6.28m,高是2m,这个谷堆的体积是多少?(得数保留两位小数)
例4、一个直角三角形的两条直角边分别是8cm和6cm,分别以两条直角边为轴旋转一周,得到两个圆锥,这两个圆锥的底面积之差是多少?
例5、求下面圆锥的体积。
(1)底面的面积是120cm²,高是15cm。
(2)底面半径是6cm,高是10cm。
演练1、一个圆锥形零件的底面积是75平方厘米,高是8厘米。求这个零件的体积。
演练2、一个圆锥形的零件,底面积是19cm²,高是12cm,这个零件的体积是多少?
例6、工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
演练1、游乐场上有一个圆锥形沙堆,底面积是12.56㎡,高是1.2m。如果用这堆沙在游乐场中铺一条宽5m,厚2cm的小路,能铺多少米?
演练2、一个铜制实心圆锥体,底面直径为8cm,高为4.5cm。每立方厘米铜重8.9g,这个铜锥重多少克?(得数保留整数)
例7、把一根底面直径为6cm,长为40cm的圆柱形铜坯,锻造成一个底面直径为20cm的圆锥形零件,这个圆锥形零件的高是多少厘米?
1、填一填。
(1)圆锥的底面( ),侧面展开图( )。
(2)从圆锥的( )到底面( )的距离是圆锥的高。
(3)圆柱的高有( )条,圆锥的高有( )条。
(4)一个圆柱的体积是28.26立方米,与它等底等高的圆锥的体积是( )立方米。
(5)一个圆锥的体积是47.1立方厘米,与它等底等高的圆柱的体积是( )立方厘米。
2、图① 小旗绕一条直角边快速转动形成的圆锥,底面半径是( )cm,高是( )cm。图②小旗绕一条直角边快速转动形成的圆锥,底面半径是( )cm,高是( )cm。
2cm
4cm 4cm
①
②
2cm
3、下面这些平面图形绕轴旋转一周,会得到什么图形,请你连一连。
有一个底面直径为20cm的圆柱形玻璃杯中装有一些水,水离杯口3cm,若将一个圆锥形的铅锤浸没到水中,水会溢出20毫升,铅锤的体积是多少cm3?
5、计算出下图圆锥的体积。
6、把一个底面半径1厘米,高9厘米的圆柱表木块加工成一个最大的圆锥。圆锥的体积是多少?要削去多少立方厘米的木料?
一个底面半径是6厘米的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9厘米的圆锥体铅锤。当铅锤从水中取出后,水面下降了0.5厘米。这个圆锥体的底面积是多少平方厘米?(π取3.14)
1、如图,一个直角梯形绕轴旋转一周后形成的立体图形的体积是多少?
第一单元 负数
1.1 负数(1)
例1、(1)零下21度,零上37度;(2)正四十三,负5度,12℃,-30℃
演练1、(1)北,负四十;(2)-1;(3)卖出230千克苹果;(4)-800元
-10℃,0℃,15℃
演练1、-10℃,0℃,10℃
例3、正数:7.3 + 87 75 +10.9 0.36 负数:-5.2 -100 -0.8
演练1、-2,8,-7,-0.12,-; 2、-5,-7,0,-3,-2;3、-2,-3,-4,-6,-8
例4、(1)3月8日,爸爸工资收入4200元,记作+4200元;
(2)3月9日,购买实木餐桌支出3000元,记作-3000元;
(3)3月10日,妈妈工资收入5100元,记作+5100元;
(4)3月11日,水电费支出165元,记作-165元。
演练1、-600m
巩固练习
1.负八;正二;五点三七,负十分之七;
正数 负数
+12 5.37
-8 - EQ \F(7,10)
2.+234 -64 0
3.D
4.< > < >
4.(135+138+142+145+150)÷5=142 cm
小东:-4cm 小丽:0 小华:+3cm小昊:+8cm
1.3 在直线上表示正数、0和负数
例1、略
演练1、图略,>3.5>2.5>1.3>﹣0.5>﹣>﹣2.9>﹣3
< < < > >
-4 -3 3 5
演练1、 A1、B-5、C-3、D0、E-1.5
1、 -8 向右移动15米;2、 +3g,-2g;3、 +4,88
1、 800,270;2、 五,一;3、 1470
向北移动3米,2米,图形略
巩固练习:
1.
小 大 小
2.(1)-5 (2)东 6 (3)西 3 (4)-5
3.
+30cm(或30cm)
4.(1)✕(2)√ (3)✕ (4)√
第二单元 百分数(二)
2.1折扣
170 演练1、 300 演练2、 12.9 演练3、 912
7000 演练1、 300 演练2、 600
七五折 演练1、 八折 演练2、八折
250 演练1、 108 演练2、 8.64元
2.5 演练1、8 演练2、400元
巩固练习:
59.6元 2、 3200 3、 八五折 4、 七五折 5、 600元 6、 15.6
2.2成数
45% 100% 55% 95% 演练1、 65% 88% 67% 85%
二成 演练1、 二成 演练2、 二成
2.34万吨 演练1、 6000 600元 演练2、 12500
巩固练习:
1.(1).10 42 (2).132% (3)二成五
2.1000×(1+25%)=1250(元)
3.(33600-28000)÷28000×100%=20%
4.2400÷12%×(1+12%)=22400(台)
2.3税率
例1、 168 演练1、 17600元 演练2、 12 演练3、 21
例2、 5% 演练1、 10% 演练2、 2%
例3、 爸爸235元,妈妈155元 演练1、 7350 演练2、 5000
巩固练习:
1.营业额 应纳税额 营业税
2.30000×5%=1500(元)
3.5÷50=10%
4.300×5%=15(万元) 300-300×5%=285(万元)
4.29%
99.8
4600
2.4 利率
例1、 720 演练1、 637.5 演练2、 7.5 1007.5 演练3、 112.5
例2、 1000元 演练1、 2000元
例3、 4.125% 演练1、 1.8% 演练2、5.76%
巩固练习:
1、22.5
2144
3.84%
4、 7000
5、2000×2.1%×2=84(元) 2000+84=2084(元)
6、20000×1.5%×1=300(元)
7、50000×(1+2.75%×3)=54125(元)
8、(527-500)÷2÷500×100%=2.7%
第三单元 圆柱与圆锥
3.1圆柱的认识
×√×√× 演练1、√×√×× 演练2、√××××√
圆柱形 演练1、×××√
巩固练习:
1.×、√、√、×;
2.略
3.2;
以AC为轴旋转,底面半径是2cm,高是1cm;
以AB旋转,底面半径是1cm,高是2cm
4.B
3.2圆柱的表面积和体积
(1)5,5,25(2)12.56(3)侧面积
演练、(1)侧面积和一个底面积,侧面积;(2) 384.65;(3)1.5
1884 演练1、(1)1.12㎡(2)100.48㎡
103.62 125.6 演练、87.92
1950平方厘米 演练1、 7.536㎡ 演练2、 628平方厘米
376.8平方厘米 演练1、 0.49千克 演练2、 125.6平方厘米
(1)底面周长的一半,底面半径,底面积,高;(2)18.84,(3)0.36
演练、(1)12.56,87.92,62.8(2)169.56(3)141.3
10990立方厘米,4710立方厘米
杯子容积50.24立方厘米,能装下牛奶
演练1、 保温杯容积0.7536升,小于1升,所以带这杯水不够喝。
演练2、10.5975吨 演练3、 7.065立方米
6750立方厘米 演练1、 450升
150.72立方厘米 演练1、 0.59dm
75.36立方厘米 演练1、 10立方分米 演练2、 160平方厘米 演练3、 109.9立方厘米
巩固练习:
1.B D C C C
2.3.14×8×3=75.36(dm2)
3.12.56÷3.14÷2=2(cm),3.14×22×2+12.56×4=75.36(cm2)
4.r=25.12÷3.14÷2=4(m),3.14×42 +25.12×4=150.72(m2),150.72×20=3014.4(kg)
5.(1)401.92平方厘米,376.8立方厘米;(2)314平方分米,392.5立方分米
6.3.14×42×8=401.92(立方厘米)
7.3.14×(6÷2)2×10=282.6(立方厘米)
8.3.14×(10÷2)2×2=157(立方厘米)
9.31.4×20×4÷(3.14×42)=50(厘米)
10.62.8立方厘米。
3.3圆锥的认识和体积
略 演练1、略
(1)顶点,圆心,1;(2)圆锥,3,底面半径;(3)6;(4)15;(5)72,24
演练、(1)等腰,20,8;(2)197.82,(3)56.52,(4)12
12.56厘米; 演练、 2.09
87.92平方厘米
(1)600立方厘米;(2)376.8立方厘米; 演练1、 200立方厘米;演练2、 76立方厘米
9.42吨 演练1、 50.24米 演练2、 671克
10.8厘米
巩固练习:
1.(1)圆 扇形 (2)顶点 圆心 (3)无数条 一条 (4)9.42 (5)141.3
2.2 4 4 2
3.略
4.3.14×(20÷2)2×3+20=962cm3
5. QUOTE ×3.14×22×3=12.56dm3
6. QUOTE ×3.14×12×9=9.42 cm3
QUOTE ×3.14×12×9=18.84cm3
7.3.14×62×0.5÷ QUOTE ÷9=18.84cm2
拓展提升:
1、549.5立方厘米
第四单元 比例
4.1 比例的意义和基本性质
例1、(1)60:10=9:15 (2)5:20=1:4 (3) (4)0.6:0.2=
演练1、(1)不可组成比例 (2)0.2:2.5=4:50 (3) (4)不可组成比例
例2、(1)4,6,10,15,4:6=10:15;(2);(3)8,;(4)3,5,15,1
演练1、(1)3,12,6,24;(2)内;(3)72
演练1、图1不能组成比例;图二能组成比例30:2=120:8;图三不能组成比例;图四能组成比例100:5=200:10
演练2、(1)边长比6:12,周长比24:48,6:12=24:48这两个比能组成比例。(2)36:144,这个比和边长比不能组成比例。
×√√××√
(1)7:8=b:a 8:7=a:b ;(2):1=a:b 1:=b:a 演练1、(1)1.2×9=3×3.6 (2)5b=9a
8,9;;1,3;
巩固练习:
1.(1)不能 因为两个比的比值不相等
(2)
(3) 不能 因为两个比的比值不相等
(4)12:1.2=1:1/10
2.1:4 2:8 1:4=2:8
3.2:3=4:6 0.6:0.8= 3:1.2=0.5:0.2
4.(1)4和9(或1和36) (只要两个数的乘积是36就行)
(2)3 (3)1和24(4和6)
发现:在比例中,两内项之积等于两外项之积.
5.(1)a×d=b×c (2)5a
6.(1)14:21=8:12 (2)A:C=D:B
7.8:32=10:40 8:10=32:40 (答案不唯一)
4.2解比例和正反比例
(1)7,9(2)(3)8:21(4)27(5)单价,数量,增加,减少,比值,正(6)每天看的页数,所用的天数,一定的,故事书的总页数
70,,1.6, 演练1、,2,20,10
32 演练1、 15000ml 演练2、 75元 演练3、 30
演练1、
例5、
每天运的质量和和天数这两种量,它们是相关联的量。
积相等,积表示的是一共运的质量。
每天运的质量×需要的天数=总质量(一定),相关联的两种量成反比例。
演练1、 成反比例,因为每天参加施工的人数×所需天数=工作总量(一定)。
演练2、(1)运货时间和运货的吨数两种量,是相关联的量;(2),他们的比值相等;(3)表示每小时运货的吨数;(4)成正比例关系,因为=每小时运货的吨数(一定)
例6、(1)工作总量和工作时间成正比例关系;(2)4.5小时能生产63吨啤酒;(3)大约需要6小时
演练1、(1)成反比例关系;(2)每小时行30千米。
巩固练习:
1.(1)x= QUOTE (2)x=3
2.(1) (2)
3.(1)成(2)成(3)不成(4)不成(5)成(6)成
4.(1)成(2)成 (3)成 (4)成 (5)不成
5.时间 时间 速度 路程 时间 路程 时间 正比例
6.(1)长 宽;(2)40×3=120 24×5=120;(3) 40×3=24×5;(4)面积;(5)面积 长 宽 反
7.20.5×400=8200(cm)=82(m)
因为c÷a=4所以周长和边长成正比例关系;s÷a=a(不确定)所以面积和边长不成比例。
9.解:设B点的高度为x米
100:60=40: x
x=2400÷100
x=24
拓展训练:
1、
路程(2)反比例关系(3)2.5时
4.3 比例尺与图形的放大与缩小
例1、 1、线段,20,1:2000000;2、 ,200;3、 1:2000000
演练1、 1、数值,,1厘米,100000000厘米;2、 5:1;3、 3;4、 4
2:1,1:2 演练1、 1、 ⑤,3:2;2、 ③,1:2
ACAC
1:5000000 演练1、 4:1 演练2、 1:100 演练3、 4:1
1.2 演练1、长4m宽3m 演练2、 12.5 演练3、 2100m
演练、
演练1、略 演练2、略
巩固练习:
(1)B(2)B
(1)位置,大小,大小,形状;(2)200
128千米 4、3厘米 5、1.2厘米 6、2.5厘米
7、80米=8000厘米 60米=6000厘米 长:8000÷2000=4(厘米) 6000÷2000=3(厘米) (图略)
8、略 9、 1728平方米 10、略 11、略
12、解:设长方形的宽为x
6:3=42:x
X=126÷6
X=21
拓展提升:1、 7.5厘米
4.4比例解决问题和自行车里的数学
35元 演练1、 12吨
速度,正,比值,4.5小时 演练1、 生产飞机的总架数,反,乘积,9天
4.5元 演练1、 20天 演练2、 840块
6千克 演练1、 2.5m 演练2、 3.2米
1、 4;2、 4;3、 7.536
约385厘米 演练1、 6.6米 演练2、 小刚一圈659.4cm,小玲一圈376.8cm,小刚的自行车蹬一圈走得远
0.80米 演练1、 60
演练1、 120天
巩固练习:
(1)时间 路程 (2)速度 (3)路程 时间 正
(1)速度 时间 (2)路程 (3)速度 时间 反
3.75
900
14
60
10
840
拓展提升:
48
第五单元 鸽巢原理
1、 2;2、 3;3、 3
演练1、 1、 3;2、 4;3、 8;4、 4
ACAC 演练1、 BAA
15 演练1、 12 演练2、 9辆 演练3、 图略;1、 2;2、 3;
33把 演练1、 31条 演练2、12 演练3、 9辆
巩固练习
(1)3(2)4,3
(1)C(2)B
3,5
40
6、9÷2=4(本)……1(本) 4+1=5(本)
7、367÷365=1(人)……2(人) 1+1=2(人)
8、15÷6=2(人)……3(人) 2+1=3(人)
拓展提升
25;2、 8
第六单元 综合与实践
6.1 数学思考
例1、 28;演练1、 66,190;演练2、 45
例2、 王阿姨是教师,刘阿姨和李叔叔是工人,丁叔叔是军人
演练1、 甲在踢足球,乙在打排球,丙在看书,丁在做作业;演练2、王涛是教师,李明是工人,孙伟是家长;
6
们; 演练1、 三角形,50个;
1、 12,16;2、 20,26;3、 y=4(x-1);演练、 1、 4,2+2+3+4;2、 2+2+3+4+5+6+7+8=37;
1、 79;2、 36,49;3、 34,55;4、 ,
巩固练习
一、1、 48;2、 6;3、 8;4、 91;
二、1、 5;2、 46;3、 30千米/小时;4、 25
6.2综合与实践
103728000吨;
演练1、15千米,7350千米,1176千克,发现:①妈妈的单位和爸爸的单位一样远;②妈妈坐地铁比爸爸开车快;③小明的交通方式最环保。
演练2、 125棵
4470元;
演练1、 1、 2、 265元
演练2、 1、 2、 买3张团体票和5张人票最省钱,一共花700元。
1、 4;2、 10;3、 3张80分或者2张1.2元;
演练1、 1、 2、 160分钟
演练2、1、78元,70.5元
1、 6g;2、 6g;3、 ; 演练1、 1、 1200;2、 1200,600,400,200;演练2、15分米;演练3、 300g
巩固练习:
(1)步行,自行车,公交车;(2)71.4%;(3)75.4%;(4)(答案不唯一)建议更多的人选择绿色出行方式,既节能环保,又有益健康。
(1)5015元;(2)1671.67元;
(1)1.8L;(2)2.5时;(3)答案不唯一
(1)53.25平方米;(2)买第一种地砖需要1092元,买第二种地砖需要1280元,买第三种地砖需要1440元。
5、寄往外地 1.20×5+2.00×1=8(元);寄往本地 0.80×5+1.20×1=5.2(元)
第一单元过关测试试卷
一、1.4、911 -0.8、-12 0
2.-3 ℃
3.+1864 低于海平面422 m
4.-2
5.< > > > > >
6.20 10 -10
二、1.× 2.× 3.√ 4.× 5.√
三、1.A 2.C 3.A 4.B 5.C
四、略。
五、1.-1 进来30人 出去12人 出去3人 进来35人
30-12-3+35=50(人)
2.-240 -2000 +1500 -1000 -1200
6800+1500-240-2000-1000-1200=3860(元)
3.70×8-480=80(m) 用-80表示
4.(1)-3时表示宇航员要进餐,宇航员-2时穿太空衣。
(2)宇航员两餐之间间隔5小时。
5.(1)莫斯科时间是2016年2月24日凌晨4:30。
(2)北京时间是2016年10月1日上午9:00。
第二单元过关测试试卷
一、1. 85 六五 25 四 2. 162 50
3.200万 4. 32000 5. 60 6. 3380
7.370 8. 225 9. 2660 10. 162
二、1.√ 2.× 3.× 4.× 5.√
三、1.C 2.C 3.D 4.C 5.D
四、1. 1908÷90%=2120(元)
2.6÷(1+20%)=5(t)
3.80×95%×1.5%+80×95%=77.14(万元)
4.8000+8000×3%×5=9200(元)
5.2145÷(1-2.5%)=2200(人)
6.(1)甲商场:3200-100×3=2900(元)
乙商场:3200×90%=2880(元)
(2)乙商场。
7.(100+80)÷(80%-70%)=1800(元)
1800×80%-100=1340(元)
8.800×80%×0.6×50%=192(元)
0.6×(1+50%)=0.9(元)
800×(1-80%)=160(支)
160×(0.9×70%-0.6)=4.8(元)
192+4.8=196.8(元)
第三单元过关测试试卷
一、1. 62.8 87.92 62.8 2. 1
3.0.785 4. 12.6 4.2
5.10.8 6. 12
7.2 25.12
8.50.24
二、1.× 2.× 3.× 4.√ 5.×
三、1.C 2.D 3.B 4.B 5.C
四、V=15×20×30-12×3.14×(10÷2)2×30=7822.5(cm3)
S=(20×15+20×30+15×30)×2-3.14×(10÷2)2+12×3.14×10×30-10×30=2792.5(cm2)
五、1.(1)3.14×(40÷2)2+3.14×40×64=9294.4(cm2)≈93(dm2)
(2)3.14×(40÷2)2×64=80384(cm3)=80.384(L)≈80(L)
2.(18.84÷3.14÷2)2×3.14×1.2×13×1.6=18.0864(t)≈18(t)
3.2 m=200 cm
3.14×10×200=6280(cm2)
4.r:62.8÷2÷3.14÷2=5(cm)
底面积:3.14×52=78.5(cm2)
侧面积:3.14×5×2×(3.14×5×2)=985.96(cm2)
表面积:985.96+78.5×2=1142.96(cm2)
5.20 cm=0.2 m 1分钟=60秒
3.14×0.222×(4×60)
=3.14×0.01×240
=7.536(m3)
6.3.14×(20÷2)2×3=942(cm3)
7.1 m=100 cm
3.14×2022−1022×100×7.8=183690(g)=183.69(kg)
第四单元过关测试试卷
一、1.40 4.8 20
2.1、2、3、4、6、8、12、24 2:4=6:12(组成的比例不唯一)
3.
4.10 9
5.正 6.反
7.1 cm 实际距离50 km 200 km
8.放大 20:1
9.18
10.1:20
二、1.√ 2.× 3.√ 4.√ 5.×
三、1.C 2.C 3.B 4.D 5.C
四、x= x=0.6 x= x=1.65
五、略
六、1.解:设这两地之间的实际距离大约是x cm。
1:15000000=3:x
x=45000000
45000000 cm=450 km
2.解:设张老师身上的血液约重x kg。
1:13=x:65 x=5
3.12×3=36(cm) 5×3=15(cm)
S=36×15=540(cm2)
C=(36+15)×2=102(cm)
4.解:设行完全程还要x小时。
=
x=2
5.解:设需要x块。
×80=•x
x=45
6.解:设实际需x天完成任务。
60×20=(60+20)x
x=15
20-15=5(天)
第五单元过关测试试卷
一、1. 2 2. 2 3. 5 4. 2
5.3 6. 3 10 9
7.4 8. 10 9. 41 10. 3
二、1.× 2.√ 3.√ 4.× 5.×
三、1.D 2.D 3.A 4.D 5.B
四、(1) ×÷
=×÷=××=
(2) ×+0.25÷-25%
=×=1
五、1. 45÷12=3……9 3+1=4(人)
2.抽出3张有如下四种情形:(1)两张偶数一张奇数;(2)两张奇数一张偶数;(3)三张奇数;(4)三张偶数。无论抽到的是上述哪种情形,一定有两个数的和是偶数。
3.3×3+1=10(只)
4.11÷(4+6)=1……1 1+1=2(名)
所以必有两名学生所借的书类型相同。
5.43÷(4+6+4+1)=2……13 2+1=3(人)
6.给小方格涂三种颜色,涂色的情况有:红黄蓝、红蓝黄、黄红蓝、黄蓝红、蓝红黄、蓝黄红,共6种,现在一共密押卷有7列,所以一定有两列的涂法是一样的。
第六单元过关测试试卷
填空
100:1;2、 2625千克,2,40;3、 立方厘米;4、 32千克;5、 反;6、 正;7、 6个,1:2=6:12;8、 36;9、 长方,周长,圆柱的高;10、 圆
判断题 √√××√
选择题 CCBCA
计算
14,,,12,,,,6,1,40
,,1726,3
应用题
64吨;2、 8小时;3、 80个;
选做题
7小时;2、 36厘米;3、 403平方分米;4、 720块
教材过关卷
一、1.3 4 负八(答案不唯一) 2.0
3.多8分 比平均成绩少10分 +5分 -3分
4.21 19 5.-3 13 6.> < = >
二、1.× 2.× 3.× 4.√
三、1.C 2.D 3.B 4.C
四、1.2 3.5 -1 -3.5
2.
+3>eq \f(5,2)>0.5>-1.5>-eq \f(9,2)
3.(1)
(2)-12 ℃
相关试卷
这是一份【精品同步】数学小升初同步培优练习六年级下册期末考试密押卷(知识梳理+含答案),共31页。试卷主要包含了填空题,判断题,选择题,计算题,动手操作,观察思考,解决问题等内容,欢迎下载使用。
这是一份【精品同步】数学小升初同步培优练习六年级下册教材过关卷(知识梳理+含答案),共31页。试卷主要包含了填空题,判断题,选择题,按要求答题,解决问题,1.解等内容,欢迎下载使用。
这是一份【精品同步】数学小升初同步培优练习六年级下册第五单元过关测试试卷(知识梳理+含答案),共30页。试卷主要包含了填空,判断,选择,下列各题,怎样简便就怎样算,解决问题,1.解等内容,欢迎下载使用。










