【精品同步】数学同步培优练习七年级下册第一讲实数及其简单应用（知识梳理+含答案）

这是一份【精品同步】数学同步培优练习七年级下册第一讲实数及其简单应用（知识梳理+含答案），共67页。

 第一讲 实数及其简单应用
实数及其简单应用





研课本 知考向




1.课程目标要求



授课内容
目标层级
1.算术平方根和平方根的概念和计算方法

2.立方根的概念和计算方法

3.无理数及实数的概念

4.实数的性质及运算




2.实时考向



本讲内容比较简单，在中考中常以简单的选择题和填空题为主。在月考中，难度稍大，会结合之前所学内容进行考察。在学习过程中，需要注重培养计算能力，本讲内容是二次根式的基础。











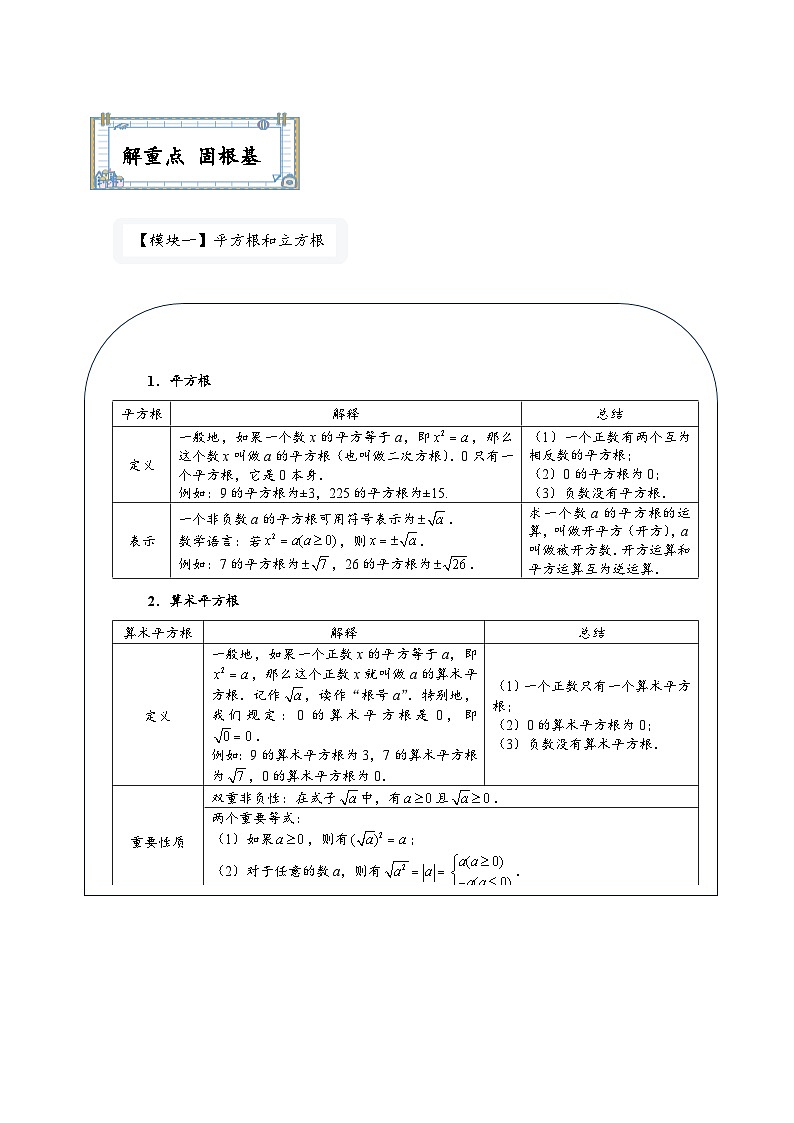
解重点 固根基




基










【模块一】平方根和立方根

就




1．平方根
平方根
解释
总结
定义
一般地，如果一个数x的平方等于a，即，那么这个数x叫做a的平方根（也叫做二次方根）．0只有一个平方根，它是0本身．
例如：9的平方根为±3，225的平方根为±15.
（1）一个正数有两个互为相反数的平方根；
（2）0的平方根为0；
（3）负数没有平方根．
表示
一个非负数a的平方根可用符号表示为．
数学语言：若，则．
例如：7的平方根为，26的平方根为．
求一个数a的平方根的运算，叫做开平方（开方），a叫做被开方数．开方运算和平方运算互为逆运算．
2．算术平方根
算术平方根
解释
总结
定义
一般地，如果一个正数x的平方等于a，即，那么这个正数x就叫做a的算术平方根．记作，读作“根号a”．特别地，我们规定：0的算术平方根是0，即．
例如：9的算术平方根为3，7的算术平方根为，0的算术平方根为0．
（1）一个正数只有一个算术平方根；
（2）0的算术平方根为0；
（3）负数没有算术平方根．
重要性质
双重非负性：在式子中，有且．
两个重要等式：
（1）如果，则有；
（2）对于任意的数a，则有．



































3．立方根
立方根
解释
总结
定义
一般地，如果一个数x的立方等于a，即，那么这个数x叫做a的立方根（也叫做三次方根）．
例如：27的立方根为3，的立方根为，0的立方根为0．
（1）任何实数都只有1个立方根；
（2）正数的立方根为正数，负数的立方根为负数，0的立方根为0．
表示
求一个数a的立方根的运算叫做开立方，a叫做被开方数，可用符号表示为，读作“三次根号a”，中“3”叫做根指数．
数学语言：若，则．
例如：7的立方根为，的立方根为．
求一个数的立方根的运算，叫做开立方，开立方与立方互为逆运算．
重要性质
（1）在式子中，a为任何实数；（2）；．




















题型一 求平方根，算术平方根


例1、 求下列各数的平方根
（1） （2） （3）

例2、（2020长芙七下第一次月考）的平方根为( )
A. B. C. D.
演练1、（2020中雅七下第一次月考）正数的平方根是__________.
演练2、（2020长郡七下期末）3的平方根是( )
A.或 B. C. D.或
例3、（2020师博七下期中）的算术平方根是( )
A. B. C. D.
演练1、（2019雅礼七下期末）9的算术平方根是（ ）
A.
B.3
C.9
D.

演练2、（2020怡雅七下第一次月考）的算术平方根是( )
A. B. C. D.
易错题1、（2020麓山七下第一次月考）的平方根是___________.
易错题2、（2020北雅七下期中）的算术平方根为（ ）
A. B. C. D.
易错题3、（2020长雅七下期中）的算术平方根是_________.

题型二 开平方及相关运算


例4、求下列各式中的值
（1） （2）（3） （4）

演练1、（2020雅实七下期中）若满足：，求的值.

题型三 求立方根，开立方及相关运算


例5、（2020立信七下第一次月考）的立方根是( )
A. B. C. D.
演练1、（2020雅实七下期中）实数等于( )
A. B. C. D.
演练2、（2019广益七下期末）的算术平方根是（ ）
A.2
B.
C.
D.
题型四 平方根和立方根的简单应用


例6、（2019青一七下期末）要使代数式有意义，则的取值范围是（ ）
A.
B.
C.
D.
演练1、（2020长雅七下期中）要使有意义，的取值范围为( )
A. B. C. D.
例7、（2020麓山七下第一次月考）下列各式，正确的是( )
A. B. C. D.
演练1、（2020长芙七下第一次月考）下列说法正确的是( )
A.的平方根是 B. C.的平方根是 D.的算术平方根是
演练2、（2020中雅七下第三次月考）下列计算正确的是( )
A. B. C. D.
例8、（2020青一七下第三次月考）下列各数中，互为相反数的是( )
A.与 B.与 C.与 D.与
演练1、（2020长芙七下第一次月考）计算：________.


【模块二】实数的概念和分类

就


1．无理数：无限不循环小数叫无理数．
2．实数：有理数和无理数统称实数．
3．实数与数轴的关系：每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都表示一个实数．即实数和数轴上的点是一一对应的.
4．实数的分类

5.实数的运算法则：
（1）在实数范围内，加、减、乘、除（除数不为 0）、乘方运算总可以进行，且结果仍然是实数.但开方运算不能无条件进行，只有正数和0才可以开偶次方.
（2）在有理数范围内适用的运算律和运算法则，在实数范围内仍然可以使用。
（3）实数的混合运算顺序：与有理数运算顺序基本相同，先乘方、开方，再乘除，最后算加减，同级运算按从左到右的顺序进行，有括号先算括号里的。





















题型五 实数的概念与分类


例9、（2020立信七下第一次月考）在实数：，，，，，中，无理数有( )
A.个 B.个 C.个 D.个
演练1、（2020麓山七下第一次月考）下列各数中，，……，，，，无理数的个数有( )
A.个 B.个 C.个 D.个
演练2、（2020长芙七下第一次月考）下列各数，，，，，其中有理数有( )
A. 个 B.个 C.个 D.个
演练3、（2020中雅七下第一次月考）在，，…，，，中，无理数有( )
A.个 B.个 C.个 D.个
例10、（2020南雅七下期中）下列说法正确的是( )
A.负数没有立方根 B.
C.无理数包括正无理数、负无理数和零 D.实数和数轴上的点是一一对应的
演练1、（2020麓山七下第一次月考）下列说法：①；②数轴上的点与实数成一一对应关系；③是的平方根；④任何实数不是有理数就是无理数；⑤两个无理数的和还是无理数；⑥无理数都是无限小数，正确的个数有( )
A.个 B.个 C.个 D.个

题型六 实数的计算


例11、（2020青一七下第一次月考）计算：
(1) (2)解方程：

演练1、（2020北雅七下期中）计算：
(1) (2)已知，求的值.


例12、（2019雅礼七下期末）计算：



演练1、（2020麓山七下第一次月考）计算:
(1) (2)


演练2、（2020怡雅七下第一次月考）计算：.



演练3、（2020青一七下期中）计算：


计算没过关，记得来加餐



1、（2020中雅七下第一次月考）计算：


2、（2020中雅七下第三次月考）计算：.

3、（2020师博七下期末）计算：



4、 （2020广益七下期末）计算:.



5、（2020中雅七下期末）



6、（2020广益七下期中）计算


【模块三】实数的估算




1．估算法：
（1）若，则；
（2）若，则；
根据这两个重要的关系，我们通常可以找距离a最近的两个平方数和立方数，来估算和的大小．例如：，则；，则．
常见实数的估算值：，，．










题型七 比较大小，估算


例13、（2019雅礼七下期末）比较大小：__________4.
演练1、（2020广益七下期末）比较大小：________.
例14、（2020青一七下第一次月考）估计的值( )
A.在和之间 B.在和之间 C.在和之间 C.在4和5之间
演练1、（2020怡雅七下第一次月考）估计的值( )
A.在和之间 B.在和之间 C.在和之间 D.在和之间
演练2、（2019广益七下期末）若，为两个连续的正整数，且，则等于（ ）
A. 6
B. 7
C. 8
D. 9


勤练习 促掌握




1、（2020广益七下期末）下列实数，，，，，中无理数有( )
A.个 B.个 C.个 D.个
2、（2020广益七下期中）在实数，，，……，，中，无理数有( )个
A. B. C. D.
3、（2020中雅七下期末）在下列各式中正确的是( )
A. B. C. D.
4、（2020立信七下第一次月考）实数的值在( )
A.和之间 B.和之间
C.和之间 D.和之间
5、（2020中雅七下第一次月考）在，，，四个数中，最大的是( )
A. B. C. D.
6、（2020中雅七下期末）的绝对值是________.
7、（2020广益七下期中）的算术平方根是__________.
8、（2020麓山七下第一次月考）若；则等式中的值为___________.
9、（2020师博七下期中）比较大小：_____(填“>”、“=”或“<”)
10、（2020师博七下期中）化简：_________.
11、（2020立信七下第一次月考）计算：________.



12、（2020南雅七下期中）计算



13、（2020师博七下期中）计算：.




14、（2020雅实七下期中）计算：




15、（2020立信七下第一次月考）计算：







七年级培优教材答案
第一讲 实数及其简单应用
题型一、求平方根、算术平方根
例1、（1） （2） （3）
例2、
演练1、 演练2、
例3、
演练1、 演练2、
易错题1、 易错题2、 易错题3、
题型二、开平方及相关运算
例4、 （1） （2） （3） （4）或
演练1、 或
题型三、求立方根、开立方及相关运算
例5、
演练1、 演练2、
题型四、平方根和立方根的简单应用
例6、
演练1、
例7、
演练1、 演练2、
例8、
演练1、
题型五、实数的概念与分类
例9、
演练1、 演练2、 演练3、
例10、
演练2、
题型六、实数的计算
例11、 （1） （2）或
演练1、（1） （2）或
例12、
演练1、（1） （2） 演练2、 演练3、
加餐练习、
1. 2. 3. 4. 5. 6.
题型七、实数的估算
例13、
演练1、
例14、
演练1、 演练2、
勤练习 促掌握
1. 2. 3. 4. 5. 6. 7. 8. 或
9. 10. 11. 12. 13. 14. 15.

第二讲 实数的综合应用
题型一、利用实数性质解题
例1、
演练1、 演练2、 演练3、
例2、
例3、
演练1、 演练2、 演练3、
例4、
演练1、 演练2、 演练3、
例5、
演练1、（1） （2）
例6、
演练1、
题型二、实数与化简
例7、
演练1、 演练2、（1） （2）
题型三、实数中其他应用
例8、 ① ② ③ ④
演练1、
例9、
例10、
题型四、实数中的新定义
例11、
演练1、
例12、 （1） （2）
例13、
演练1、 演练2、
例14、
演练1、（1） （2） （3）
勤学习 促掌握
1. 2. 3. 4. 5. 6. 7.
8. （1） （2） 9. 10.

第三讲 实数的综合应用
题型一、平面直角坐标系与点的坐标
例1、
例2、
演练1、 一
例3、
演练1、 演练2、 演练3、
例4、
演练1、 演练2、
例5、
演练1、 演练2、 演练3、
例6、
例7、
题型二、坐标系中的平移
例8、
演练1、 演练2、
例9、
例10、
演练1、
例11、
演练1、 演练2、 演练3、
题型三、坐标系中的对称、位置
例12、
演练1、（1） （2），为任意实数 （3）
例13、
演练1、
题型四、坐标系的面积
例14、 （1） （2） （3）或
例15、 （1），， （2）
（3） 或
演练1、（1），, （2）略
（3）
演练2、 （1），， （2）
勤学习 促掌握
1. 2. 3. 4. 5. 6.
7. 8. 9. ，
10. （1），， （2）.
11. （1）略 （2），，
第四讲 坐标系中的规律探究与新定义
题型一 一般规律问题
例题 1. 2. 3.
演练 1. 2.
例题 4.
演练 1.
题型二 正方形中的规律问题
例题 5.
演练 1. 2.
例题 6.
演练 1.
题型三 旋转类规律问题
例题 7.
演练 1.
例题 8.
题型四 坐标系中的新定义
例题 9. 10.（1）①，；②；（2）“识别距离”最小值为，
11. （1）；（2）；（3）
12. （1）；（2）；（3），
勤练习，促掌握
1. 2. 3. 4. 5. 6.（1）；（2）；（3）等腰三角形，理由如下：根据题意可求出
第五讲 坐标系中的综合应用
题型一、坐标与面积
例1、 （1） （2）
（3）设

， 或
例2、①
②
③当在线段上时,当在点左侧时
题型二、坐标与角度、面积的结合
例3、（1）
（2）的平分线和的平分线交于点



设,则
作，则
又





（3）存在某一时刻，使的面积等于长方形面积的，
作 轴于，，


例4、 (1)∵且
∴，
又∵点关于轴对称点为点
∴点的坐标
(2)∵为中点，为中点
∴为重心
∴
又∵
∴
(3)由题意可得：
∴
又∵
∴
又∵
∴
题型三、坐标与平行、面积的结合
例5、 (1)由题意得：，，
∴，，
∴点、、的坐标为：，，
(2)不变，
如图2，过点做
∵，
∴
∴，
∵，∴
∵，∴
∴
∵、分别平分，
∴，
∴
(3)设点
①若点位于轴正半轴上且，过点作轴，则
，，


由题意得：，即，解得.此时点
②若点位于轴负半轴上，则，




由题意：，即，解得，此时
③若点位于轴正半轴上且，此时显然不成立
综上所述：存在或使的面积等于的面积的

例6、 (1)∵
∴，
∴，
∴，
∴
(2)存在点或使，证明如下：
设坐标为，在

∴，
∴坐标为或
(3) (过点作轴平行线即可)

例7、 （1）


(2)




或
（3）设旋转t s后OA与CN平行
①当时








②当时




同理可得

（舍）
③时，如图2


同理可得：


综上所述或
题型四、坐标系中的定值问题
例8、 (1)
（2）


（3） 定值为3
例9、 （1）


又

（2） 当入射角为时，反射光线与平行
（3）
题型五、坐标系中的动态问题分析
例10、 （1）
（2）根据平移性质得： ,
∴ ，解得：AC=6，
（3）∵AC∥x轴，AC=6,∴C的坐标为（6，3），根据平移性质得D(4,7),
，
∴,∵B点横坐标为2，
又∵ ,
∴当P点在M,N点时等式成立，
满足条件的时间t如下：
1） 开始到第一次掉头时， ；
2） 第一次掉头到第二次掉头时， ；
3） 第二次掉头到第三次掉头时， ；
4） 第三次掉头到第四次掉头时， ；
5） 第四次掉头到第五次掉头时，（不符合题意），
∴符合的时间有：0s，18s，27s，33s，37.5s
例11、 （1）
（2） ① ② ③
（3） 或
勤练习 促掌握
1. （1） （2） （3）
2. (1)
(2) 或
(3)
3. (1)，
(2)的大小不变
延长、交于点
∵直线与直线垂直相交于
∴
∴
∴
∵、分别是和的角平分线
∴，
∴
∴
∴
∴
∵、分别是和的角平分线
∴
∴
(3)∵与的角平分线相交于
∴，
∴
∵、分别是和的角平分线
∴
在中
∵有一个角是另一个角的倍，故有：
①，，
②，，(舍)
③，，
④，，(舍)
∴为或
4. （1）
（2） （提示：方程解题）
（3） ①当时，;当时，
②

第六讲 二元一次方程（组）及其解法和应用
题型一 二元一次方程（组）的定义
例题 1.
演练 1. 2.
例题 2. 3.
演练 1.
例题 4.
演练 1.
题型二 二元一次方程（组）的解的概念
例题 5.
演练 1. 2. 3.
题型三 二元一次方程（组）的解法
例题 7.
演练 1. 2.
例题 8.
演练 1. 2.
例题 9.（1）；（2）
演练 1.（1）；（2） 2.（1）；（2）
3.（1）；（2）
例题 10.
演练 1. 2. 3.
例题 11.（1）；（2）
演练 1.（1）；（2）
题型四 二元一次方程组一般应用
例题 12. 13. 14.
题型五 古文中的二元一次方程组
例题 15.
演练 1.
题型六 图形中的二元一次方程组
例题 16.
演练 1. 2.设加工竖式纸盒个，横式纸盒个。依题意，得
解得
题型七 二元一次方程组综合应用
例题 17.（1）设排球单价元，实心球单价元。依题意，得解得；（2）（元）
演练 1.（1）设购进甲型口罩个，乙型口罩个。依题意，得
解得；（2）设每袋乙型口罩打折。，，四折。
2.（1）购进黑色文化衫件，白色文化衫件。依题意，得解得；
（2）（元）
3.（1）设型车进价为元，型车进价为元。依题意，得解得；
（2）方案①型车：2辆，型车：15辆；方案②型车：4辆，型车：10辆；
方案③型车：6辆，型车：5辆。（3）方案①利润最大，最大利润是元。
勤练习，促掌握
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.（1）；（2） 13.（1）；（2）
14.设长方形地砖的长为，宽为。依题意，得解得。
15.（1）设茄子的种植面积为公顷，西红柿的种植面积为公顷。依题意，得解得；（2）（万元）
第七讲 含参二元一次方程（组）的解法
题型一、特殊方程组的解法
例1、
演练1、
例2、 、、
演练1、
例3、 、、
演练1、 、、
演练2、 （1） （2）、、、
例4、
演练1、
例5、
题型二、已知解求参数
例6、
演练1、 演练2、
题型三、已知解的关系求参数
例7、
演练1、 演练2、 演练3、 演练4、略
题型四、同解问题与错解问题
例8、
演练1、
例9、
演练1、（1）、 （2）、
题型五、整数解问题
例10、
例11、 （1）、 （2）
题型六、二元一次方程组中的新定义
例12、 （1） （2）
（3） ①当，时，不存在解坐标
②当，时，存在无数个解坐标
演练1、（1） （2） （3）
勤练习 促掌握
1. 2. 3.
4. （1） （2）
5. 6. 、、原式
7. （1）①不是②的“中雅方程组”
（2）或或
（3）
第八讲 一元一次不等式与不等式组
题型一、不等式的概念和性质
例1、
例2、
演练1、 演练2、 演练3、 演练4、
题型二、一元一次不等式的概念和解法
例3、
例4、
演练1、
例13、
演练1、
例5、
演练1、
例6、
例7、
演练1、 演练2、
例8、
题型三、一元一次不等式组的概念和解法
例9、 （1） （2）
演练1、 演练2、 演练3、
例10、
演练1、 演练2、 演练3、 整数解为、、
例11、
例12、
演练1、
勤练习 促掌握
1. 2. 3. 4. 5. 6.
7. 8. 9.
10. （1） （2） 11.
12. （1） （2） 13. （1） （2）
14. 非整数解的和为 15.
第九讲 一元一次不等式组的实际应用
题型一、实际应用
例1、
演练1、（1）奖品每件元，奖品每件元
（2）奖品最多购买件
题型二、方案选择
例2、 （1）甲种客车载客量为人，乙种客车载客量为人
（2）两种租车方案①甲车辆，乙车辆②甲车辆，乙车辆，第①种方案最省钱
演练1、 （1）老师有人，学生有人；
（2）辆
（3）种，元
例3、 （1）大型渣土车每次运土方吨，小型渣土车每次运土方吨
（2） ①大型渣土车辆，小型渣土车辆，总费用为元
②大型渣土车辆，小型渣土车辆，总费用为元
③大型渣土车辆，小型渣土车辆，总费用为元
④大型渣土车辆，小型渣土车辆，总费用为元
最少需要花费元。
演练1、（1）类货车每辆补贴油费元，类货车每辆补贴油费元
（2）最少为元。
演练2、（1）甲货车每次满载能运输吨物资，乙货车每次满载能运输吨物资
（2）安排甲货车辆，乙货车辆最节省费用，最少为元
例4、 （1）型号的扫地车每周可以处理吨，型号的扫地车每周可以处理吨。
（2）一共有三种方案：
①购买型扫地车辆，型扫地车辆
②购买型扫地车辆，型扫地车辆
③购买型扫地车辆，型扫地车辆
方案①所需资金最少，最少为万元。
例5、 （1）改造个甲种型号大棚需要万元，改造个乙种型号大棚需要万元
（2）一共有三种方案：
①改造个甲种型号大棚，个乙种型号大棚
②改造个甲种型号大棚，个乙种型号大棚
③改造个甲种型号大棚，个乙种型号大棚
方案③所需资金最少，最少为万元。
例6、 （1）甲种笔每支元，乙种笔每支元
（2）共有种进货方案。
演练1、（1）甲种文具每件元，乙种文具每件元
（2）一共有三种方案：
①购买甲种文具件，乙种文具件
②购买甲种文具件，乙种文具件
③购买甲种文具件，乙种文具件
演练2、（1）每件甲产品的成本价为元，每件乙产品的成本价为元
（2）一共有三种方案：
①购进件甲产品，件乙产品
②购进件甲产品，件乙产品
③购进件甲产品，件乙产品
方案③利润最大，最大利润为万元。
例7、 （1）每本数学文化的价格为元，每本文学名著的价格为元
（2）一共有三种方案：
①购进数学文化本，文学名著本
②购进数学文化本，文学名著本
③购进数学文化本，文学名著本
演练1、（1）甲种奖品的单价为元，乙种奖品的单价为元
（2）一共有三种方案：
①购买甲种奖品个，乙种奖品个
②购买甲种奖品个，乙种奖品个
③购买甲种奖品个，乙种奖品个
方案①最省钱
例8、 （1）购买种树每颗需要元，购买种树每颗需要元
（2）一共有三种方案：
①购买种树棵，购买种树棵
②购买种树棵，购买种树棵
③购买种树棵，购买种树棵
演练1、（1）购买种树苗每颗需要元，购买种树苗每颗需要元
（2）一共有三种方案：
①购进种树苗棵，购进种树苗棵
②购进种树苗棵，购进种树苗棵
③购进种树苗棵，购进种树苗棵
方案①最省钱，最少工钱为元
例9、 （1） （2） （3），为或
例10、 （1）①③ （2） （3）
勤练习 促掌握
1. （1）奖品的单价为元，shshan商品的单价为元
（2）至少购买zh种商品个
2. （1）一件文化衫元，一套明信片元
（2）购买文化衫件，购买明信片套
3. （1）帐篷有个，食品包有个
（2）方案一：安排辆乙种货车；方案二：安排辆甲种货车，辆乙种货车；方案三：安排辆甲种货车，辆乙种货车；方案四：安排辆甲种货车，辆乙种货车；方案五：安排辆甲种货车，辆乙种货车；
（3）选用方案运费最少，最少是元。
4. （1）甲商品件，乙商品件
（2）乙商品最低售价为每件元

第十讲 不等式组的综合应用
题型一、已知范围求解
例1、
演练1、
演练2、 演练3、
演练4、 （1） （2） （3） 为
演练5、（1） （2） （3）
题型二、整数解问题
例2、
例3、
演练1、 演练2、
题型三、不等式中的新定义
例4、 （1）① ② （2） （3） （4）或
演练1、（1） （2） （3）或
演练2、（1）① ② （2） （3）或
例5、 （1） （2）① ② ③
例6、 （1）① ② （2）或 （3）
例7、 （1） （2） （3）
例8、 （1） （2）或 （3）
例9、 （1）②是 （2）或 （3）
例10、 （1） 是 （2） （3）
例11、 （1）存在“雅含”关系，是的“子式”
（2） （3）
勤练习 促掌握
1. 2. 3. 4.
5. （1） （2） 6.（1） （2）
7.（1） （2） （3）或
8. （1） （2） （3）

第十一讲 调查统计和直方图
题型一、统计相关的概念
例1、 每名考生的数学成绩
演练1、
例2、
例3、
演练1、 演练2、 演练3、③
例4、
例5、
例6、
演练1、 演练2、 演练3、
例7、
题型二、数据的描述
例8、
演练1、 演练2、
例9、 （1）人 （2） （3） 名
演练1、（1）名 （2） （3）名
演练2、（1）名 （2） （3）名
演练3、（1）踢毽子人数为名 （2） （3）人
演练4、（1） （2）略 （3）万人
演练5、（1）吨 （2） （3）吨

勤练习 促掌握
1. 2. 3.
4. （1）名 （2） （3）万户
5. （1） （2）略 （3）名
6.（1）， （2）略 （3）人
第十二讲 三角形及其简单应用
题型一、三角形的稳定性
例1、
演练1、
例2、
题型二、三角形的边
例3、
演练1、 演练2、 演练3、 演练4、
例4、
演练1、 演练2、
例5、
演练1、 演练2、 演练3、 演练4、
题型三、三角形的角
例6、
例7、
演练1、 演练2、
例8、
例9、
演练1、 八边形 演练2、
例10、
演练1、 十二 演练2、 演练3、
例11、
例12、 （1） （2）
演练1、 （1） （2）
题型四、两大模型的应用
例13、 （1） （2） （3）
例14、 （1）在和中



（2） 由（1）得


例15、 （1）
（2）
例16、 （1）、、
（2）
（3）
例17、
演练1、 演练2、
勤练习 促掌握
1. 2. 3. 4. 5. 6.
7. 8.三角形得稳定性 9. 10.
11. 12. 13.（1） （2）
14.
15.（1）
（2）
（3）



第十三讲 全等三角形
题型一 全等三角形的性质
例题 1.
演练 1. 2.
例题 2. 3.
演练 1.
例题 4.
演练 1.（1）先求证即可证明；（2）由（1）可得，所以
例题 5.
演练 1.（1）∵∴；（2）∵是等腰直角三角形，∴垂直平分
2.（1）∵∴；（2）由（1）可知∴是等腰三角形，
例题 6.（1）∵∴；（2）设点到的距离为，，
演练 1.（1）∵∴；（2）
例题 7.（1）∵∴；（2），∵∴，
演练 1.（1）∵平分，∴
又，
∴，
∵，度，∴度
又度，∴度，度
（2）由题知，∴
∵度，∴，∴度，∴度
又平分，∴
又，∴，∴
2. （1）∵∴；（2）且，
由（1）可知,；
（3） .
例题 8.①②③ 9. 10.
11.
演练 1.（1）1；（2）过点作，∵∴，∴
2.方法一：过点作，∵∴，
方法二：过点作，过点作,∵∴，∴，
方法三：过点作交的延长线于点，∴，
例题 12.延长至点，使，∵
∴，在中，﹤,﹥
∴﹤﹤
演练 1. 2.②③④
例题 13.截长：












补短：延长至点使，∵∴，∵,，∴，
演练 1.延长到点，使，连接



例题 14.













15.














16. ③⑤⑥
勤练习，促掌握
1. 2. 3. 4. 5. 6.（1）由题可知,所以；（2）
7.（1）；（2）；（3）当，当。
8.






9.【证明】∵
∴，(两直线平行，内错角相等)
∵
∴
又∵
∴
∴
∴，(等式的性质)
∴
10.【证明】(1)由题意可知，
∴，
又
在和中
，，
∴，∴
∵，
∴，∴，即
(2)∵，∴ ①
∵，∴
∵，
∴ ②
∴由①、②得：，
11.










12.











13.





























第十三讲 全等三角形中的模型
题型一 一线三垂直
例题 1.


















2.（1）∵,,，∴，；（2）连接，,∴，∵，∴
3.过点，分别作，先求证可知；再求证可知；∴，∴，是的中线
4.（1）①，；②，求证；
（2）
题型二 角平分线模型
例题 5.










6.














7.



















演练 1.









2. 3. 4. 5.（1）；（2）；
（3）在上截取，连
在和中

∴
∴，
又，
∴
∴
∴
题型三 手拉手模型
例题 8.















演练 1.①②③④
例题 9.








10.














11.（1）∵∴,
（2）∵∴，
题型四 半角模型
例题 12.










13.














演练 1.（1）①；②相等，；（2）①
2. （1）；（2）
勤练习，促掌握
1.
2.










3.【解析】(1)证明：∵，
∴
在和中

∴
∴
则，，
∴平分
(2)由(1)知，又
∴


4.

















5.











6. （1）；（2），求证
7.



























8.





























第十四讲 全等三角形综合
题型一 全等中的新定义
例题1.(1)∵四边形是互补等对边四边形
∴
在和中

∴
(2)∵四边形是互补等对边四边形
∴
又由(1)
∴
∴
∵
∴
∴
(3)证明：如图③所示：过点、分别作的延长线与的垂线，垂足分别为、
∵四边形是互补等对边四边形，
∴，
又
∴
又∵，
∴
在和中

∴
∴
在和中

∴
∴
∵
∴
∴
∵
∴
∵，
∵















例题2.





























例题3.


题型二 全等三角形中的大综合
例题4.（1）证明：如图，设
则，
在中，∵
∴
∴
∴
∴平分
（2）证明：如图，过点作于点，过点作交的延长线于点
∵
∴
∴，
∴
在和中，

∴
∴
在和中，

∴
∴
（3）解：如图，连接
在和中

∴
∴
∵
∴
∴
∵
∴
∵
∴
∴















例题5.





























例题6.





























例题7.(1)、、
(2)∵，；又
∴或
当在线段上时，如图①.连接、，则
∵
∴，.又为中点
∴，且
又
∴
又
∴
∴，
∵
∴
即轴
∴.
当在线段的延长线上时，如备用图
∴
由①得，
∴
又
∴
∴，
∵
∴
即轴
∴
综上所述：点的坐标为或
(3)设，.过点作直线轴.
∵
∴
又，
∴
∴，且
∵
∴
∴轴
∴.
∴当从点沿轴负方向运动时，点从点沿直线向下运动
∵为中点
∴
又
∴
∴
∴
∵
∴，且
∴
∴
∴
∴点从运动至.路径长为

例题8.




















勤练习，促掌握
1.①③④
2.(1)证明：证明即可
(2)解：①当时，点在线段上，点在线段上
，
∴
∴(不合题意，舍去)
②当时，点在线段上，点在线段上
，
∴
∴
综上，
综上所述当时，与全等
(3)解：∵
∴
∵
∴
∵
∴
∴
∵，
∴



3.





























4.





















（3）