

所属成套资源:(2023年专用)2021+2022年山东省小升初数学真题题型汇编(通用版)(含解析)
- 题型一 选择题57题(二)——(2023专用)2021+2022年山东省各地区小升初真题题型汇编(通用版)(含解析) 试卷 1 次下载
- 题型三 填空题58题(一)——(2023专用)2021+2022年山东省各地区小升初真题题型汇编(通用版)(含解析) 试卷 1 次下载
- 题型三 填空题63题(二)——(2023专用)2021+2022年山东省各地区小升初真题题型汇编(通用版)(含解析) 试卷 1 次下载
- 题型二 判断题76题(一)——(2023专用)2021+2022年山东省各地区小升初真题题型汇编(通用版)(含解析) 试卷 1 次下载
- 题型五 解答题54题(一)——(2023专用)2021+2022年山东省各地区小升初真题题型汇编(通用版)(含解析) 试卷 2 次下载
题型三 填空题59题(三)——(2023专用)2021+2022年山东省各地区小升初真题题型汇编(通用版)(含解析)
展开
这是一份题型三 填空题59题(三)——(2023专用)2021+2022年山东省各地区小升初真题题型汇编(通用版)(含解析),共15页。试卷主要包含了填空题等内容,欢迎下载使用。
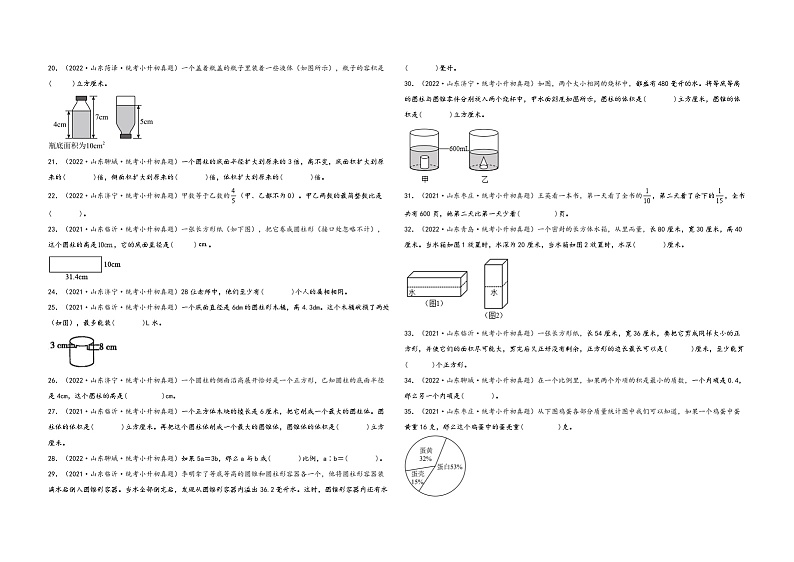
小升初真题练:题型三 填空题59题(三)(2023年专用)山东省近两年小升初真题题型汇编亲爱的同学们,小升初的复习已经开始,特为大家准备了近两年山东省各地区的小升初考试真题,尤其以常考易错真题为主,大家可以进行题型专项训练,提高成绩,做到举一反三!题型数量大,大家不用一次性做完,可以分批次进行,预祝大家成绩步步高升!一、填空题1.(2022·山东临沂·统考小升初真题)4.5平方米=________平方分米 5.02升=________升________毫升5立方分米6立方厘米=________立方分米 公顷=________平方米2.(2022·山东菏泽·统考小升初真题)一个圆锥的底面积是12平方厘米,高是3厘米,则它的体积是( )立方厘米。3.(2022·山东青岛·统考小升初真题)用圆规画一个周长31.4厘米的圆,圆规两脚尖之间的距离是( )厘米。如果这个圆的半径扩大到原来的2倍,那么它的周长扩大到原来的( )倍,面积扩大到原来的( )倍。4.(2022·山东菏泽·统考小升初真题)一个圆柱和圆锥等底等高,体积相差8dm3,这个圆锥的体积是( )dm3,圆柱的体积是( )dm3。5.(2021·山东济宁·统考小升初真题)王伯伯把20000元存入银行,定期3年,年利率是2.75%,到期时他共取回( )元。6.(2021·山东临沂·统考小升初真题)一个圆锥的体积是48立方厘米,高是8厘米,底面积是( )平方厘米。7.(2021·山东济宁·统考小升初真题)30米比( )米多20%;( )比64少30%。8.(2022·山东青岛·统考小升初真题)一个等腰三角形,其中两个内角和是130°,它的顶角可能是( )或( )。9.(2022·山东青岛·统考小升初真题)运动员进行跑步练习,同样的距离小明用时1分半,小强用时100秒,小明与小强速度的最简整数比是( )。10.(2022·山东菏泽·统考小升初真题)如果y=,则x与y成( )比例;如果y=,则x与y成( )比例。11.(2022·山东聊城·统考小升初真题)鸡兔同笼,共有35个头,94只脚,兔子有( )只。12.(2022·山东济宁·统考小升初真题)在一幅比例尺是8∶1的精密零件图纸上,量得图纸上零件长40m,这个零件实际长( )mm。13.(2021·山东济宁·统考小升初真题)两个等高的圆柱和圆锥,如果圆柱与圆锥的底面半径这比是2:1,那么圆柱和圆锥的体积最简比是________:________.14.(2022·山东菏泽·统考小升初真题)观察如图,找规律。第7幅图中有( )个○,有( )个△。15.(2021·山东济宁·统考小升初真题)一个漏水的水龙头每天要白白地流掉约10千克水。照这样计算,这个漏水的水龙头2021年第一季度要白白流掉( )千克水。16.(2022·山东青岛·统考小升初真题)一个精密零件的长是3毫米,画在图纸上长是9厘米,这张图纸的比例尺是( )。17.(2021·山东济宁·统考小升初真题)把线段比例尺改写成数值比例尺是 。18.(2021·山东菏泽·统考小升初真题)如图,已知长方体的长是15.7cm,高是8cm,圆柱底面半径是( )cm,长方体的表面积比圆柱的表面积增加( )cm2,圆柱的体积是( )cm3。19.(2021·山东济宁·统考小升初真题)如图,一张三角形纸片被撕去了一个角,撕去的这个角是( )度,原来这张纸片的形状是( )三角形,也是( )三角形。20.(2022·山东菏泽·统考小升初真题)一个盖着瓶盖的瓶子里装着一些液体(如图所示),瓶子的容积是( )立方厘米。21.(2022·山东聊城·统考小升初真题)一个圆柱的底面半径扩大到原来的3倍,高不变,底面积扩大到原来的( )倍,侧面积扩大到原来的( )倍,体积扩大到原来的( )倍。22.(2022·山东济宁·统考小升初真题)甲数等于乙数的(甲、乙都不为0)。甲乙两数的最简整数比是( )。23.(2021·山东临沂·统考小升初真题)一张长方形纸(如下图),把它卷成圆柱形(接口处忽略不计),这个圆柱的高是,它的底面直径是( )。24.(2021·山东济宁·统考小升初真题)28位老师中,他们至少有( )个人的属相相同。25.(2021·山东临沂·统考小升初真题)一个底面直径是6dm的圆柱形木桶,高4.3dm。这个木桶破损了两处(如图),最多能装( )L水。26.(2022·山东济宁·统考小升初真题)一个圆柱的侧面沿高展开恰好是一个正方形,已知圆柱的底面半径是4cm,这个圆柱的高是( )cm。27.(2021·山东临沂·统考小升初真题)一个正方体木块的棱长是6厘米,把它削成一个最大的圆柱体。圆柱体的体积是( )立方厘米。再把这个圆柱体削成一个最大的圆锥体,圆锥体的体积是( )立方厘米。28.(2022·山东聊城·统考小升初真题)如果5a=3b,那么a与b成( )比例,a∶b=( )。29.(2021·山东临沂·统考小升初真题)李明拿了等底等高的圆锥和圆柱形容器各一个,他将圆柱形容器装满水后倒入圆锥形容器。当水全部倒完后,发现从圆锥形容器内溢出36.2毫升水。这时,圆锥形容器内还有水( )毫升。30.(2022·山东济宁·统考小升初真题)如图,两个大小相同的烧杯中,都盛有480毫升的水。将等底等高的圆柱与圆锥零件分别放入两个烧杯中,甲水面刻度如图所示,圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。31.(2021·山东枣庄·统考小升初真题)王英看一本书,第一天看了全书的,第二天看了余下的,全书共有600页,她第二天比第一天少看( )页。32.(2022·山东青岛·统考小升初真题)一个密封的长方体水箱,从里而量,长80厘米,宽30厘米,高40厘米。当水箱如图1放置时,水深为20厘米,当水箱如图2放置时,水深( )厘米。33.(2021·山东临沂·统考小升初真题)一张长方形纸,长54厘米,宽36厘米,要把它剪成同样大小的正方形,并使它们的面积尽可能大,剪完后又正好没有剩余,正方形的边长最长可以是( )厘米,至少能剪( )个正方形。34.(2022·山东聊城·统考小升初真题)在一个比例里,如果两个外项的积是最小的质数,一个内项是0.4,那么另一个内项是( )。35.(2021·山东枣庄·统考小升初真题)从下图鸡蛋各部分质量统计图中我们可以知道,如果一个鸡蛋中蛋黄重16克,那么这个鸡蛋中的蛋壳重( )克。36.(2022·山东青岛·统考小升初真题)一杯糖水中含糖10克,水90克,若使糖水的浓度不变。续添2克糖后,应再添( )克水。37.(2021·山东临沂·统考小升初真题)把一个圆柱体木料横切成两个圆柱(图1),表面积增加了25.12cm2,纵切成两个半圆柱(图2),则表面积增加了48cm2,原来这个圆柱的体积是( )cm3。38.(2022·山东聊城·统考小升初真题)一个长方体,一个圆柱和一个圆锥,它们的底面积和体积分别相等,如果长方体的高是9厘米,圆柱的高是__________厘米,圆锥的高是__________厘米。39.(2022·山东枣庄·统考小升初真题)“众志成城,抗击疫情”,4月3日17点山东省援沪医疗队在济南集结,乘坐“复兴号”列车奔赴上海支援疫情防控工作,1.5小时行了全程的。照这样的速度,列车约( )点到达终点站。40.(2021·山东菏泽·统考小升初真题)用小棒按照如下的方式摆图形,摆一个六边形需要6根小棒,摆4个需要________根小棒,摆n个需要________根小棒。41.(2022·山东菏泽·统考小升初真题)如图,把圆柱切开拼成一个近似的长方体,已知长方体的长是6.28m,高是3m。这个圆柱的底面半径是( )m,侧面积是( )m2。42.(2021·山东临沂·统考小升初真题)观察下列图形,找规律再填空。照这样摆下去,第6个图中有( )个黑色方块,第n个图中黑色方块有 ( )个。43.(2022·山东枣庄·统考小升初真题)一个圆柱和圆锥的底面积和高分别相等,已知圆柱体积比圆锥的体积多12cm3,圆柱的体积是( )cm3,圆锥的体积是( )cm3。44.(2022·山东枣庄·统考小升初真题)枣庄市全员核酸检测的时候,“大白天使”张丽和李华共同为某小学全体师生做核酸检测,张丽完成了40%,李华比张丽多做了80个,李华做了( )个核酸检测。45.(2022·山东济南·小升初真题)做一批零件,师傅需要用8小时完成,徒弟需要用12小时才能完成,师傅合作,( )小时能完成。46.(2022·山东枣庄·统考小升初真题)袋子里装有红、黄、蓝、绿四种颜色的小球各10个(小球除颜色外完全相同),每次取一个,若保证取出的球中必须有三个同色的,至少要取出( )次.47.(2022·山东济南·小升初真题)观察如图,想一想。第7幅图有( )个点子,第n幅图的点子总数是( )个。48.(2022·山东枣庄·统考小升初真题)x和y是两种相关联的量,如果,则x和y成( )比例关系;如果8x=7y,那么x和y成( )比例关系。49.(2022·山东济南·统考小升初真题)把11个苹果全部分给4个小朋友,总有一个小朋友至少分到( )个苹果。50.(2022·山东青岛·统考小升初真题)一个停车场停有四轮小汽车和三轮电动车共24辆。如果这些车共有86个轮子,那么停车场里有( )辆小汽车和( )辆电动车。51.(2022·山东济南·小升初真题)一个平行四边形和一个三角形等底等高,已知平行四边形的面积是42dm2,三角形的面积是( )dm2。52.(2022·山东济南·统考小升初真题)某商场的所有商品一律打八五折销售,妈妈准备为苗苗买一双标价240元的凉鞋,她需要付( )元,如果她买了一件折后价为170元的连衣裙,这件连衣裙的标价是( )元。53.(2022·山东济南·统考小升初真题)如图所示,把底面半径是2厘米、高10厘米的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的底面积是( )平方厘米,体积是( )立方厘米。54.(2022·山东临沂·统考小升初真题)一条环形小路,外圆半径是18米,内圆半径是16米,这条环形小路的面积是________平方米。要在这条小路的外围栽树,两棵树之间的距离是1.57米,要栽________棵树。55.(2022·山东菏泽·统考小升初真题)公园挖了一个直径是60m的圆形池塘,池塘的周长是( )m,沿池塘的周围每隔6.28m种一棵树,共可种( )棵树。56.(2022·山东临沂·统考小升初真题)一个圆锥的体积是76立方厘米,底面积是19平方厘米,这个圆锥的高是( )厘米。57.(2022·山东菏泽·统考小升初真题)一个长3cm,宽2cm的长方形,按3∶1放大,得到的图形的面积是( )cm2,周长是( )cm。58.(2021·山东济宁·统考小升初真题)在比例尺是20∶1的图纸上量得一个零件的直径是6厘米,这个零件直径的实际长度是( )毫米。59.(2021·山东枣庄·统考小升初真题)有两个圆,它们的面积之差是2平方厘米,已知小圆周长是大圆周长的90%,小圆的面积是( )平方厘米。 参考答案1. 450 5 20 5.006 6000【分析】高级单位平方米化低级单位平方分米乘进率100;5.02升看作5升与0.02升之和,把0.02升乘进率1000化成20毫升;把6立方厘米除以进率1000化成0.006立方分米,再加5立方分米;高级单位公顷化低级单位平方米乘进率10000。【详解】4.5平方米=4.5×100平方分米=450平方分米 5.02升=5升+0.02×1000毫升=5升+20毫升=5升20毫升5立方分米6立方厘米=5立方分米+6÷1000立方分米=5立方分米+0.006立方分米=5.006立方分米 公顷=×10000平方米=6000平方米【点睛】单位换算能够沟通不同单位间的联系,不同属性的单位之间的进率不同,需要加以熟记。2.12【分析】根据圆锥的体积公式,直接将数据代入公式,求出它的体积即可。【详解】×12×3=12(立方厘米)所以,它的体积是12立方厘米。【点睛】本题考查了圆锥的体积,圆锥的体积=×底面积×高。3. 5 2 4【分析】半径决定圆的大小,根据圆的周长公式:C=2,那么r=C÷÷2,据此求出半径,因为圆周率一定,所以圆的周长与半径成正比例,圆的半径扩大到原来的几倍,圆的周长就扩大到原来的几倍;圆的面积的比等于半径平方的比。据此解答。【详解】31.4÷3.14÷2=10÷2=5(厘米)根据分析得,如果这个圆的半径扩大到原来的2倍,那么它的周长扩大到原来的2倍,面积扩大到原来的2×2=4倍。【点睛】此题主要考查圆的周长公式、面积公式的灵活运用,关键是熟记公式。4. 4 12【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积差相当于圆锥体积的(3-1)倍,由此可以求出圆锥的体积,进而求出圆柱的体积,据此解答。【详解】8÷(3-1)=8÷2=4(dm3)4×3=12(dm3)【点睛】此题主要考查等底等高的圆柱与圆锥体积之间关系的灵活运用。5.21650【分析】本金是20000元,存期是3年,年利率是2.75%,通过利息的计算公式:利息=本金×利率×存期,求出利息,再加上本金,即可得解。【详解】20000+20000×2.75%×3=20000+550×3=20000+1650=21650(元)到期时他共取回21650元。【点睛】此题的解题关键是利用计算利息的公式来求解,注意到期时他共取回的钱指的是本金和利息。6.18【详解】略7. 25 44.8【分析】把要求的这个米数看作单位“1”,单位“1”未知,要求的这个米数的(1+20%)是30米,根据分数除法的意义,用30除以(1+20%),计算后即可得解;求的这个数相当于64的(1-30%),求一个数的百分之几是多少,用乘法,列式:64×(1-30%),计算后即可得解。【详解】30÷(1+20%)=30÷120%=25(米)64×(1-30%)=64×70%=44.8【点睛】此题的解题关键是掌握已知比一个数少百分之几的数是多少,求这个数和求比一个数少百分之几的数是多少的计算方法。8. 50° 80°【分析】三角形的内角和是180°,当两个底角的和是130°时,则顶角为180°-130°=50°;当顶角和一个底角的和是130°时,则底角为180°-130°=50°,顶角为130°-50°=80°,据此解答即可。【详解】一个等腰三角形,其中两个内角和是130°,它的顶角可能是50°或80°。【点睛】本题主要考查了三角形的内角和以及等腰三角形的特征,解答时要分情况考虑。9.10∶9【分析】1分半=90秒,小明和小强所用的时间比为90∶100=9∶10。再根据路程一定时,速度比和时间比相反,可知小明和小强的速度比为10∶9,据此解答即可。【详解】运动员进行跑步练习,同样的距离小明用时1分半,小强用时100秒,小明与小强速度的最简整数比是10∶9。【点睛】明确路程一定时,速度比和时间比相反是解答本题的关键。10. 正 反【分析】依据正、反比例的意义,即若两个量的比值一定,则这两个量成正比例;若两个量的乘积一定,则这两个量成反比例,从而可以判断x和y成什么比例。【详解】如果y=,则=6,比值一定,x和y成正比例关系;如果y=,则xy=6,乘积一定,x和y成反比例关系。【点睛】解答此题的主要依据是正、反比例的意义。11.12【分析】假设都是兔,根据脚的只数与实际只数的差,除以每只鸡与兔的腿数的差,再求鸡的只数,进而求出兔的只数,据此解答。【详解】假设都是兔,则鸡有:(35×4-94)÷(4-2)=(140-94)÷2=46÷2=23(只)兔有:35-23=12(只)【点睛】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。12.5000【分析】根据“实际距离=图上距离∶比例尺”代入数值求出实际距离。【详解】40∶=5(m)5m=5000mm【点睛】此题主要考查比例尺、图上距离、实际距离三者的关系式:比例尺=图上距离∶实际距离,灵活变形列式解决问题。13. 12 1【分析】由圆柱的体积公式和圆锥的体积公式根据公式推算得出.【详解】由题意,假设圆柱和圆锥的体积分别是V1、V2,r1:r2=2,所以.14. 13 36【分析】观察图形可知,○的个数位:序号数减1的差乘2,然后再加上1即可;△的个数位:序号数减1的差的平方。据此填空即可。【详解】第7幅图中○的个数有:(7-1)×2+1=6×2+1=12+1=13(个)第7幅图中△的个数有:(7-1)2=62=36(个)【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。15.900【分析】第一季度包括1月、2月和3月,2021年是平年,2月有28天,1月和3月都有31天,据此可求出第一季度共有多少天,再用第一季度的天数乘每天流掉的水的重量即可。【详解】(31×2+28)×10=90×10=900(千克)则2021年第一季度要白白流掉900千克水。【点睛】本题考查平年和闰年,明确平年的2月有28天是解题的关键。16.30∶1##【分析】依据比例尺的意义,图上距离与实际距离的比即为比例尺,即可求解。【详解】9厘米∶3毫米=90毫米∶3毫米=90∶3=30∶1这幅图的比例尺是30∶1。【点睛】此题主要考查比例尺的意义,解答时要注意单位的换算。17.1∶5000000【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。【详解】50千米=5000000厘米比例尺是1∶5000000。【点睛】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。18. 5 80 628【分析】观察图可知:长方体的长是圆柱底面周长的一半,长方体的高就是圆柱的高,根据圆的周长公式,先用周长的一半乘2求出底面周长,再除以3.14求出圆柱的底面直径,再除以2,即可求出圆柱的底面半径;拼成的近似的长方体的面积比原来圆柱体面积增加了两个侧面面积(半径纵切面),每个侧面的长是圆柱的高,宽是圆柱的底面半径,再根据长方形的面积公式求解即可;然后根据圆柱的体积公式:V=Sh,代入数据求解即可。【详解】15.7×2÷3.14÷2=15.7÷3.14=5(cm)8×5×2=40×2=80(cm2)3.14×52×8=3.14×25×8=628(cm3)【点睛】解决本题关键是明确拼成的长方体与圆柱之间的关系,找出增加的表面积是以底面半径和高为边长的两个长方形的面的面积。19. 67 锐角 等腰【分析】三角形的内角和为180°,因此用180°减去67°后,再减去46°即可,最后根据三个角的度数将三角形分类即可。【详解】180°-67°=113°113°-46°=67°90°>67°=67°>46°因此原来这张纸片的形状是锐角三角形,也是等腰三角形。【点睛】此题考查的是三角形的内角和,以及三角形的分类,应熟练掌握。20.60【分析】由图可知:图2空白圆柱的高为7-5=2(厘米),瓶子的容积=高为4厘米的圆柱的体积+高为2厘米的圆柱的体积,再根据圆柱的体积公式V=Sh计算,可据此解答。【详解】10×4+10×(7-5)=40+10×2=40+20=60(立方厘米)【点睛】利用体积不变的特性,把不规则图形转化成规则图形来计算,是解此题的关键。21. 9 3 9【分析】假设出原来圆柱的底面半径和高,根据圆的面积公式S=πr2,圆柱的侧面积公式S=2πrh,圆柱的体积公式V=πr2h,求出圆柱的底面积、侧面积、体积的变化情况。【详解】假设原来圆柱的底面半径为3,现在圆柱的底面半径为9,圆柱的高为h。底面积:(92π)÷(32π)=81π÷9π=9侧面积:(2π×9×h)÷(2π×3×h)=18πh÷6πh=3体积:(92π×h)÷(32π×h)=81πh÷9πh=9所以,一个圆柱的底面半径扩大到原来的3倍,高不变,底面积扩大到原来的9倍,侧面积扩大到原来的3倍,体积扩大到原来的9倍。【点睛】掌握圆柱的侧面积和体积计算公式是解答题目的关键。22.4∶5【分析】根据甲数等于乙数的(甲、乙都不为0),可写出等量关系式为:甲数=乙数×(甲、乙两数均不为0),根据比例的性质改写成比例的形式,再化简即可解答。【详解】甲数=乙数×(甲、乙两数均不为0)甲数∶乙数=∶1=(×5)∶(1×5)=4∶5【点睛】解答此题应根据比例基本性质的逆运算进行解答。23.10【分析】长方形的长是圆柱底面周长,用底面周长÷π=底面直径。【详解】31.4÷3.14=10(厘米)【点睛】关键是熟悉圆的特征,理解长方形和圆柱之间的关系。24.3【分析】把12属相看作12个“抽屉”,把28人“看作物体的个数”,根据抽屉原理可得:28÷12=2(人)…4(人),从最极端情况分析:如果每种属相都有2人,则还有4人,则至少有2+1=3人的属相相同。【详解】由分析可知:2+1=3(人)则28位老师中,他们至少有3个人的属相相同。【点睛】此题属于典型的抽屉原理习题,解答此类题的关键是找出把谁看作“抽屉个数”,把谁看作“物体个数”,然后根据抽屉原理解答即可。25.98.91【分析】通过观察图形可知,这个木桶破损处距离桶口最深8cm,即0.8dm,那么最多盛水的高为(4.3-0.8)dm;根据圆柱的体积公式:V=πr2h,代入数据计算即可。注意单位的换算:1dm=10cm,1dm3=1L。【详解】8cm=0.8dm3.14×(6÷2)2×(4.3-0.8)=3.14×9×3.5=28.26×3.5=98.91(dm3)98.91 dm3=98.91L【点睛】明确木桶最多能装水的高度是到木桶的最高破损点,掌握圆柱的体积公式以及体积、容积单位之间的换算是解题的关键。26.25.12【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形(或正方形),这个长方形的长等于圆柱的底面周长,宽等于圆柱的高;当圆柱的侧面沿高展开是一个正方形时,这个圆柱的底面周长和高相等;根据圆的周长公式C=2πr,代入数据计算即可。【详解】2×3.14×4=6.28×4=25.12(cm)【点睛】本题考查圆柱侧面展开图的特征、圆的周长公式,关键是知道圆柱的侧面展开恰好是一个正方形时,这个圆柱的底周长和高相等。27. 169.56 56.52【分析】由题意知,削成的最大圆柱体的底面直径是6厘米,高也是6厘米,可利用V=Sh求出它的体积,再把圆柱削成最大的圆锥体,则圆锥是与圆柱等底等高的,圆锥的体积就是圆柱体积的,要求圆锥的体积可用圆柱的体积乘即可。【详解】3.14×(6÷2)2×6=3.14×9×6=169.56(立方厘米)169.56×=56.52(立方厘米)圆柱体的体积是169.56立方厘米;圆锥体的体积是56.52立方厘米。【点睛】此题是考查圆柱、圆锥的体积计算,在求圆锥体积时不要忘了乘。28. 正 3∶5【分析】将等积式化成比例式,求出比值,再判定a与b成正比例还是成反比例。【详解】因为5a=3b,所以a∶b=3∶5=(一定)。a与b的比值一定,a与b成正比例。【点睛】本题考查了比例的基本性质和正比例、反比例的辨识,属于基础知识,需熟练掌握。29.18.1【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积差相当于圆锥体积的(3-1)倍,根据已知一个数的几倍是多少,求这个数,用除法解答。【详解】36.2÷(3-1)=36.2÷2=18.1(毫升)【点睛】此题考查的目的是理解掌握等底等高的圆柱和圆锥体积之间的关系及应用。30. 120 40【分析】根据题意可知,把圆柱放入烧杯中,上升部分水的体积就等于这个圆柱的体积,再根据等底等高的圆锥的体积是圆柱体积的,据此求出圆锥的体积。【详解】600-480=120(毫升)120毫升=120立方厘米120×=40(立方厘米)【点睛】此题考查的目的是理解掌握利用“排水”法求物体体积的方法及应用,等底等高的圆柱与圆锥体积之间的关系及应用。31.24【分析】找准数量关系,分别算出第二天和第一天看的数量,再用第一天看的数量减去第二天看的数量,即可计算解答。【详解】第一天:600×=60(页)第二天:(600-60)×=540×=36(页)60-36=24(页)【点睛】找准数量关系,掌握求一个数的几分之几的计算方法,是解决此题的关键。32.40【分析】图一长方体底面长是80厘米、宽是30厘米,此时水位高20厘米,根据长方体体积公式,求出水的体积。由于不论是怎样放置,水的体积不变,所以图二中水的体积和图一水的体积相等。图二底面长40厘米、宽30厘米,用水的体积除以底面积,求出此时水深多少厘米。【详解】80×30×20÷(30×40)=48000÷1200=40(厘米)所以,当水箱如图2放置时,水深40厘米。【点睛】本题考查了长方体的体积,长方体体积=底面积×高,那么高=体积÷底面积。33. 18 6【详解】54=2×3×3×336=2×2×3×3所以54和36的最大公因数是2×3×3=18,故正方形边长最长可以是18厘米;(54÷18)×(36÷18)=3×2=6(个)34.5【分析】最小的质数是2,在一个比例里,如果两个外项的积是2,则两个内项的积也是2,用2除以0.4即可求出另一个内项。【详解】2÷0.4=5【点睛】本题考查了比例的基本性质:两个外项的积等于两个内项的积。35.【分析】从扇形统计图可以看出来,一个鸡蛋中蛋黄的质量占32%,已知蛋黄重16克,已知部分求整体,蛋壳的质量占15%。根据一个数乘分数的意义用乘法解答即可。【详解】16÷32%×15%=50×15%=7.5(克)【点睛】本题考查扇形统计图、百分数有关的计算,注意已知部分求整体用除法,已知整体求部分用乘法。36.30【分析】用糖的质量10克除以糖水的质量10+90=100(克),再乘100%,先求出原来糖水的浓度。要保持糖水浓度不变,添2克糖后糖有12克,用12克除以浓度,求出此时水有多少克,再将这个水的克数减去原有的90克,求出应添水多少克。【详解】10÷(10+90)×100%=10÷100×100%=10%(2+10)÷10%=12÷10%=120(克)120-90=30(克)所以,若使糖水的浓度不变。续添2克糖后,应再添30克水。【点睛】本题考查了百分率,糖的浓度=糖的质量÷糖水质量×100%。37.75.36【分析】根据图1的方式切成两个圆柱,表面积就会增加25.12cm2,表面积增加的是两个切面的面积,每个切面的面积与原来圆柱的底面积相等,据此可以求出圆柱的底面半径,进而求出圆柱的高,再根据圆柱的体积公式解答;图2沿直径方向切成两个半圆柱,切面是两个长方形,长等于圆柱的高,宽等于圆柱的底面直径,表面积增加的48平方厘米,是两个切面的面积,由此可以求出一个切面的面积。【详解】圆柱的底面积:25.12÷2=12.56(cm2)底面半径的平方:12.56÷3.14=4因为2的平方是4,所以圆柱的底面半径是2cm圆柱的高:48÷2÷(2×2)=24÷4=6(cm)体积:3.14×22×6=3.14×4×6=75.36(cm3)【点睛】此题解答关键是根据纵切、横切,求出圆柱的底面半径和高,再利用圆柱的体积公式解答。38. 9 27【详解】解:(1)长方体和圆柱的体积都是V=sh,当V和S分别相等时,高也是相等的,即圆柱的高是9厘米;(2)圆柱的体积是V=sh,圆锥的体积是V=sh,当V和S分别相等时,高是不等的,圆锥的高是圆柱高的3倍;圆锥的高是:9×3=27(厘米)。39.20【分析】已知列车1.5小时行了全程的,根据已知一个数的几分之几是多少,求这个数,用除法求出行完全程一共需要多少小时,再根据时间的推算方法,求出几点达到终点。【详解】1.5÷=3(小时)17+3=20(点)列车约20点到达终点站。【点睛】本题主要考查了分数除法应用题,明确已知一个数的几分之几是多少,求这个数,用除法求解。40. 21 5n+1【分析】摆一个六边形需要6根小棒,以后每增加一个六边形,就增加5根小棒,所以摆成n个六边形就需要:6+5(n-1)=5n+1根小棒,据此即可解答.【详解】摆一个六边形需要6根小棒,以后每增加一个六边形,就增加5根小棒,所以摆成n个六边形就需要5n+1根小棒;摆4个需要5×4+1=21(根)即摆4个需要21根小棒,摆n个需要5n+1根小棒。故答案为:21;5n+141. 2 37.68【分析】根据题意,把圆柱切开,再拼成一个近似的长方体,这个长方体的长等于圆柱体的底面周长的一半,长方体的高等于圆柱的高,长方体的宽等于圆柱体的半径,已知长方体的长是6.28m,那么乘以2即可得出圆柱的底面周长,根据底面周长公式:C=2πr,即可得出底面半径,然后再根据圆柱侧面积公式:S侧=Ch,以此解答。【详解】6.28×2=12.56(m)12.56÷3.14÷2=4÷2=2(m)12.56×3=37.68(m2)【点睛】此题的关键是理解把圆柱切开,再拼成一个近似的长方体,这个长方体的长等于圆柱体的底面周长的一半,长方体的高等于圆柱的高。42. 14 2(n+1)【分析】根据图形的变化规律:图1是4个黑方块,图2比图1多两个黑方块,图3比图1多(3-1)×2个黑方块,那么第6个图中黑色方块比第1个图多(6-1)×2个,第n个图中黑色方块比第1个图多(n-1)×2个,据此解答即可。【详解】第6个图中黑色方块有:4+(6-1)×2=4+5×2=4+10=14(个)第n个图中黑色方块有:4+(n-1)×2=4+2n-2=2n+2=2(n+1)(个)故答案为:14;2(n+1)【点睛】此题考查的是图形的变化规律,主要培养学生的观察力和总结能力。43. 18 6【分析】圆柱和圆锥等底等高,则圆锥的体积是圆柱的。已知圆柱体积比圆锥体积多12cm3,那么12cm3占圆柱体积的,用除法即可求出圆柱体积;圆柱体积×即可求出圆锥体积。【详解】==18(cm3)18×=6(cm3)【点睛】本题考查了圆柱和圆锥的体积关系,即圆锥的体积等于与它等底等高圆柱体积的。44.240【分析】根据题意,把全体师生看作单位“1”,张丽完成了40%,李华完成了(1-40%),李华比张丽多做了80个对应的分率是(1-40%-40%),用除法求出全体师生人数,再乘上李华完成的百分数,解答即可。【详解】1-40%-40%=60%-40%=20%80÷20%×(1-40%)=80÷20%×60%=400×60%=240(个)【点睛】此题主要考查了百分数乘除法的意义的应用,要熟练掌握,解答此题的关键是找准单位“1”。45.【分析】把这批零件的总数看作单位“1”,根据工作效率=工作总量÷工作时间,计算师徒二人的工作效率,再用工作总量除以二人工作效率的和,求工作时间。【详解】1÷(1÷8+1÷12)=1÷(+)=1÷=(小时)【点睛】本题主要考查简单的工程问题,关键是利用工作总量、工作时间和工作效率的关系做题。46.9【分析】利用的知识点是抽屉原理.【详解】每次取出一个,取8次时4种颜色的球至少各有两个,要想保证有三个同色的至少要再取一次,也即是8+1=9.47. 49 n2【分析】由题可知,1×1=1,2×2=4,3×3=9,4×4=16……规律:第几幅图点子数就是几的平方;据此解答即可。【详解】7×7=49(个)第n幅图的点子总数是n2个。【点睛】解答本题关键是找到变化规律。48. 反 正【分析】两种相关联的量,若其比值一定,两种量成正比例关系;若其乘积一定,两种量成反比例关系,据此解答。【详解】如果,则xy=56,x与y的乘积一定,x与y成反比例关系。如果8x=7y,则,x与y的比值一定,x与y成正比例关系。【点睛】根据正比例意义以及辨别,反比例意义以及辨别进行解答。49.3【分析】把11个苹果分给4个小朋友,即将这4个小朋友当作4个抽屉,将这11个苹果放入这四个抽屉,利用抽屉原理最差情况:要使每个人分到的苹果最少,只要使每个抽屉的元素数尽量平均分即可。【详解】11÷4=2(个)……3(个)2+1=3(个)所以总有一个小朋友至少分到3个苹果。【点睛】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑。50. 14 10【分析】设停车场共有x辆小汽车,则有(24-x)辆电动车,每辆汽车有4个轮子,每辆三轮电动车有3个轮子,根据题意有关系式:每辆汽车的轮子个数×汽车车辆数+每辆电动车的轮子个数×电动车车辆数=86,列方程求解即可。【详解】解:设停车场共有x辆小汽车,则有(24-x)辆电动车。4x+(24-x)×3=864x+72-3x=86x=86-72x=1424-14=10(辆)即停车场里有14辆小汽车和10辆电动车。【点睛】本题主要考查用方程解决鸡兔同笼问题,关键根据车的辆数设未知数,根据轮子个数列方程。51.21【分析】三角形的面积是与其等底等高的平行四边形面积的一半,用42除以2,即可求出三角形的面积,据此解答。【详解】42÷2=21(dm2)【点睛】此题考查的目的是理解掌握等底等高的三角形和平行四边形面积之间的关系及应用。52. 204 200【详解】240×85%=204(元)170÷85%=200(元)53. 12.56 125.6【分析】(1)这个长方体的底面积其实就是圆柱体的底面积,因此求出圆柱体的底面积即可。(2)长方体的体积与圆柱体的体积相等,只是形状发生了变化,但体积是相等的。【详解】(1)3.14×22=12.56(平方厘米)(2)3.14×22×10=12.56×10=125.6(立方厘米)答:这个长方体的底面积是12.56平方厘米,体积是1256立方厘米。故答案为:12.56,125.6【点睛】本题考查了学生的转化思想,转化后的图形与原图形密不可分,同时考查了圆柱体的体积公式及表面积公式的运用情况。54. 213.52 72【分析】根据圆环的面积计算公式(R2-r2)×π即可解答;在封闭线路上植树,棵数与段数相等,即:棵数=间隔数,先计算小路外围的周长:3.14×2×18=113.04(米),然后计算间隔数即植树棵数:113.04÷1.57=72(棵)。【详解】(182-162)×3.14=68×3.14=213.52(平方米)3.14×2×18÷1.57=113.04÷1.57=72(棵)【点睛】将圆环的面积与植树问题相结合,如能画示意图,则可以辅助理解;注意题干里的字眼:在这条小路的“外围栽树”,指的是在外圆的一周上植树。55. 188.4 30【分析】根据圆的周长公式:C=πd,据此求出池塘的周长;在封闭的圆形池塘周围植树,植树的棵树=间隔数,根据间隔数=圆的周长÷间隔长度,据此解答即可。【详解】3.14×60=188.4(m)188.4÷6.28=30(棵)【点睛】本题考查圆的周长,熟记公式是解题的关键。56.12【分析】题目中知道圆锥的体积和底面积,根据体积公式V锥=Sh代入数据求解即可。【详解】3×76÷19=12(厘米)一个圆锥的体积是76立方厘米,底面积是19平方厘米,这个圆锥的高是12厘米。【点睛】此题考查了圆锥的体积公式的灵活应用。57. 54 30【分析】把图形按照3∶1放大,就是将图形的每一条边放大到原来的3倍,放大后图形与原图形对应边长的比是3∶1,用原长方形的长和宽乘扩大的倍数,求出扩大后的长和宽,再根据长方形周长公式:(长+宽)×2和面积公式:长×宽,代入数据计算即可。【详解】3×3=9(cm)2×3=6(cm)(9+6)×2=15×2=30(cm)9×6=54(cm2)【点睛】本题考查了图形的放大与缩小,图形放大或缩小的倍数是指对应边放大或缩小的倍数。58.30【分析】根据图上距离∶实际距离=比例尺,已知图上距离和比例尺,可求出实际距离=图上距离∶比例尺,据此代入数值进行计算即可。【详解】6÷20=0.3(厘米)=30(毫米)这个零件直径的实际长度是30毫米。【点睛】本题考查比例尺,明确图上距离∶实际距离=比例尺是解题的关键。59.【分析】小圆周长是大圆周长的90%,则小圆的半径是大圆半径的90%,确定小圆与大圆半径比,再根据半径比平方以后的比是面积比,确定两圆面积比,面积差÷对应份数,求出一份数,再乘小圆面积对应份数即可。【详解】根据小圆的半径是大圆半径的90%,小圆半径∶大圆半径=9∶10,小圆面积∶大圆面积=9²∶10²=81∶100。2÷(100-81)×81=2÷19×81=(平方厘米)【点睛】关键是理解比的意义,掌握圆的面积公式。
相关试卷
这是一份题型二 填空题65题(三)——(2023专用)2021+2022年陕西省各地区小升初真题题型汇编(通用版)(含解析),共18页。试卷主要包含了填空题等内容,欢迎下载使用。
这是一份题型二 填空题60题(二)——(2023专用)2021+2022年陕西省各地区小升初真题题型汇编(通用版)(含解析),共15页。试卷主要包含了填空题等内容,欢迎下载使用。
这是一份题型二 填空题60题(一)——(2023专用)2021+2022年陕西省各地区小升初真题题型汇编(通用版)(含解析),共13页。试卷主要包含了填空题等内容,欢迎下载使用。









