
2023年江苏省连云港市灌南县小升初数学模拟测试卷
展开2023年江苏省连云港市灌南县小升初数学模拟试卷
一、理解与填空。(每空1分,10分)
1.光每秒传播299792千米,约是 万千米。(保留整数)
2.
500ml= L | 0.85平方千米= 公顷 |
3.把24个桃子平均分给8只小猴,每只小猴分到这些桃子的,每只小猴分到 个桃子。
4.李大爷家有鹅45只,鹅的只数是鸭的3倍,鸡比鸭多8只,鸡有 只.
5.从3根7厘米的小棒和3根8厘米的小棒中选出4根围成一个平行四边形,这个平行四边形的周长是 厘米。
6.小明忘记存包箱密码,但他回忆出密码可能是55500000,50050005,50000505,50000550这四个数中的一个,并确信密码这个数只读一个“零”,这个密码是 。
7.如果xy+5=7.5,x和y成 比例.
8.做一个生日蛋糕需要用0.56千克白色奶油、0.25千克彩色奶油和0.26千克面粉,假设有足够的面粉和彩色奶油,用8千克白色奶油,最多可以做 个这种生日蛋糕。
二、优化与选择。(每小题1分,20分)
9.如图的大正方形表示“1”,其中阴影部分表示的是 ( )
A.0.05 B.0.50 C.5 D.50
10.一个三角形中三个角度数的比是1:2:3,这是( )三角形。
A.锐角 B.直角 C.钝角 D.无法确定
11.数a,b在数轴上的位置如图所示,下列式子结果最大的是( )
A.a÷b B.a+b C. D.a×(a+b)
12.下列图形中,不是轴对称图形的是( )
A.平行四边形 B.正三角形 C.圆 D.等腰梯形
13.某地白天最高温度是零上8℃,记作+8℃,夜间的最低温度比白天最高温度下降了10℃,夜间最低温度记作( )℃
A.﹣10 B.﹣2 C.﹣8 D.﹣18
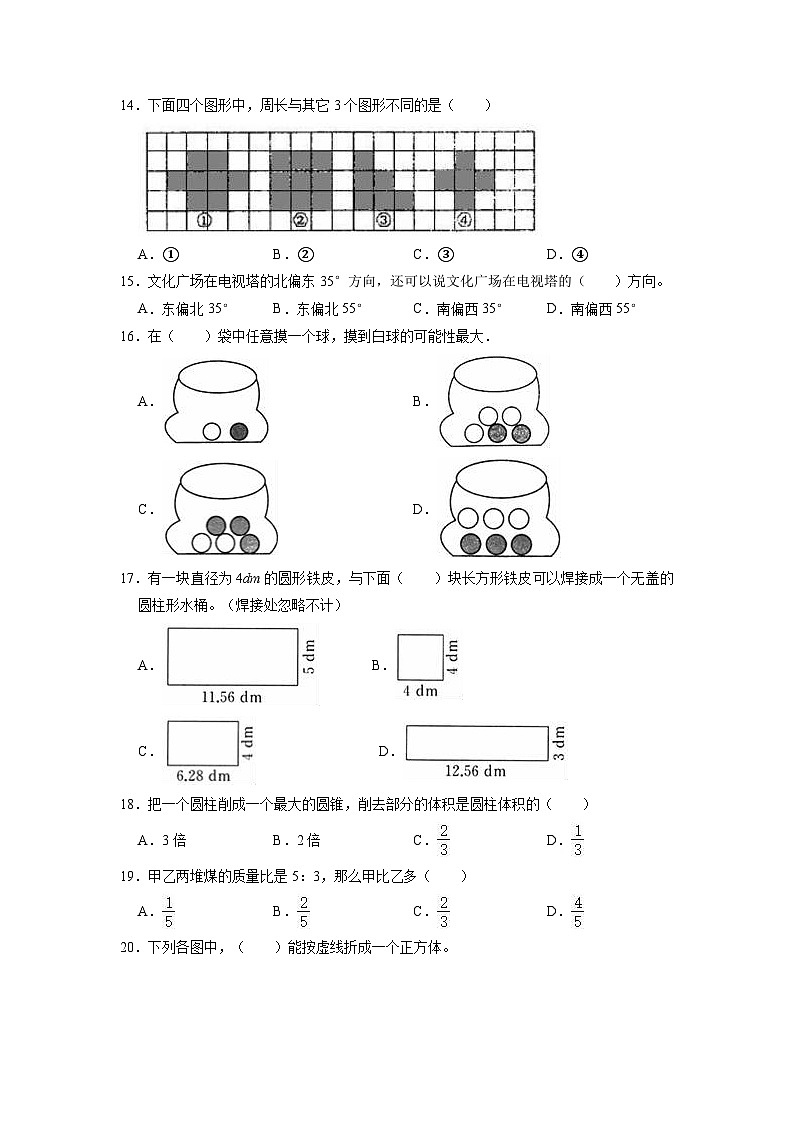
14.下面四个图形中,周长与其它3个图形不同的是( )
A.① B.② C.③ D.④
15.文化广场在电视塔的北偏东35°方向,还可以说文化广场在电视塔的( )方向。
A.东偏北35° B.东偏北55° C.南偏西35° D.南偏西55°
16.在( )袋中任意摸一个球,摸到白球的可能性最大.
A. B.
C. D.
17.有一块直径为4dm的圆形铁皮,与下面( )块长方形铁皮可以焊接成一个无盖的圆柱形水桶。(焊接处忽略不计)
A. B.
C. D.
18.把一个圆柱削成一个最大的圆锥,削去部分的体积是圆柱体积的( )
A.3倍 B.2倍 C. D.
19.甲乙两堆煤的质量比是5:3,那么甲比乙多( )
A. B. C. D.
20.下列各图中,( )能按虚线折成一个正方体。
A. B.
C. D.
21.王老师今年42岁了,下面( )接近王老师今年的年龄。
A.500分 B.500时 C.500周 D.500月
22.甲数÷0.99=乙数×0.99(甲、乙两数均不为0),那么( )
A.甲数>乙数 B.甲数<乙数 C.甲数=乙数 D.无法确定
23.把一个圆柱形木块切削成一个和它等底等高的圆锥模型。圆锥的体积是圆柱体积的( )
A. B. C.3倍 D.9倍
24.用可以表示以下两个图形之间的关系( )
A.平行四边形和长方形 B.梯形和三角形
C.平行四边形和梯形 D.正方形和梯形
25.两根彩带,甲剪去全长的,乙剪去米,两根彩带都剩下米。原来的两根彩带,( )
A.甲长 B.乙长 C.一样长 D.无法确定
26.如图是一只停泊在平静水面上的小船,它的“倒影”应是图中的( )
A. B. C. D.
27.把10克糖溶在100克水中,糖占糖水的( )
A. B. C. D.
28.在对折好的纸上剪两个洞,打开后的图形是( )
A. B. C. D.
三、运算与求值。(33分)
29.(9分)解方程。
12.5%x+10=18 | x=13 |
30.(9分)仔细算一算,怎样简便就怎样计算。
4.9×6.4+15.1×6.4 | (826﹣370)÷38×6 | 19÷[(+)÷] |
31.(9分)递等式计算。
×× | ×÷ | ÷14÷ |
32.(6分)估算.
896+309≈
723÷89≈
四、调查与统计。(6分)
33.(6分)2005年,我国对523个城市的空气质量状况进行了监测,结果如下表.
空气质量情况 | 城市个数 | 占监测城市的百分之几(百分号前保留一位小数) |
达到二级(含二级)标准以上 | 344 | 65.8% |
达到三级标准 |
| 25.4% |
未达到三级标准 | 46 |
|
该情况选用 统计图表示比较合适.请你完成统计图和统计表.
五、判断与说理。(8分)
34.(4分)乐久小学对本校学生参加爱心捐款活动情况进行了统计,并绘制了如图的扇形统计图。
(1)已知该校学生共捐款4万元,求四年级学生捐款多少元?
(2)从这幅图中能否得出“五年级学生捐款数最多”的结论吗?为什么?
35.(4分)一块长方形地里种了三种蔬菜,白菜地占整块地的一半,萝卜地和菠菜地同样大(如图),白菜地的面积是多少平方米?萝卜地的面积是多少平方米?
六、情境与应用。(23分)
36.(4分)汽车每小时行驶多少千米?
37.(4分)探索梯形时,将梯形转化为学过的图形,通过比较转化前后图形的面积得到梯形的面积。若将梯形转化为学过的三角形(如图),怎么得出梯形的面积公式呢?请写出你的思考过程。
38.(4分)爸爸杀好鱼后,妈妈开始烧鱼.她有条理地洗鱼、切鱼、切姜片、洗锅、把锅烧热、把油烧热、煎烧,直到鱼烧熟共花了17分钟(见图).
你能不能设计一个巧妙合理的新顺序,使妈妈少花些时间?请用方框图表示出来.
39.(4分)学校劳技社团制作了一个水箱,相关数据如图1所示;打开水龙头,给这个水箱注水,注水时间和水位高度如图2所示,其中B点的水位高度是A点水位高度的2倍。
(1)由图可知, 秒后水箱注满了水,此时应该关闭水龙头。
(2)以0.1升/秒的速度往水箱里注水,可求得这个水箱的容积是 升。
(3)通过计算求出这个水箱的高度h。(单位:分米)
40.(7分)为了更加了解学生的体质健康状况,2021年4月份芜湖市各小学开展了体质健康测试活动,如表是李平同学的部分信息,请根据信息完成下面各题。
姓名 | 身高(cm) | 年龄(岁) | 体重(kg) |
李平 | 150 | 12 | 60 |
(1)标准体重是反映和衡量一个人健康状况的重要标志之一。世界卫生组织提出男生的标准体重计算方法是:标准体重kg=(身高cm﹣80)×70%。请你计算一下李平同学的标准体重应该是多少?
(2)如表是人的不同体重状况的参考标准,请帮李平同学算出他的体重状况。
体重状况 | 参考标准 |
正常体重 | 不超出标准体重10% |
超重 | 超出标准体重10%~20% |
轻度肥胖 | 超出标准体重20%~30% |
中度肥胖 | 超出标准体重30%~50% |
重度肥胖 | 超出标准体重50%以上 |
(3)根据李平同学的情况,你想对他说什么?
参考答案与试题解析
一、理解与填空。
1.【分析】省略“万”后面的尾数就是四舍五入到万位,即把万位后面的千位上的数进行四舍五入,再在数的后面写上“万”字。
【解答】解:299792≈30万
故答案为:30。
【点评】本题主要考查整数求近似数,注意求近似数时要带计数单位。
2.【分析】低级单位毫升化高级单位升除以进率1000;
高级单位平方千米化低级单位公顷乘进率100。
【解答】解:
500ml=0.5L | 0.85平方千米=85公顷 |
故答案为:0.5,85。
【点评】本题是考查体积(容积)的单位换算、面积的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
3.【分析】把这些桃子的个数看作一个整体,把它平均分成8份,每只小猴子分得1,每分是这些桃子的;求每份是几个,用总个数除以8。
【解答】解:把24个桃子平均分给8只小猴,每只小猴分到这些桃子的
24÷8=3(个)
每只小猴分到3个桃子。
故答案为:,3。
【点评】此题是考查分数的意义。把一个整体平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数。求平均每小猴子分得的个数,根据整数除法即可解答。
4.【分析】有鹅45只,鹅的只数是鸭的3倍,用45除以3即可求出鸭的只数,又根据鸡比鸭多8只,用鸭的只数加上8即可求解.
【解答】解:45÷3+8
=15+8
=23(只)
答:鸡有 23只.
故答案为:23.
【点评】解答本题的关键是根据整数除法的意义求出鸭的只数,然后再进一步解答即可.
5.【分析】根据平行四边形的对边相等,所以需要选2根7厘米的小棒和2根8厘米的小棒,据此解答即可。
【解答】解:7×2+8×2
=14+16
=30(厘米)
答:这个平行四边形的周长是30厘米。
故答案为:30。
【点评】熟练掌握平行四边形的特征,是解答此题的关键。
6.【分析】根据整数中“零”的读法,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零,分别读出各数再作选择。
【解答】解:5550 0000读作:五千五百五十万;
5005 0005读作:五千零五万零五;
5000 0505读作:五千万零五百零五;
5000 0550读作:五千万零五百五十。
故答案为:50000550。
【点评】本题主要是考查整数的读法,分级读或借助数位顺序表读能较好的避免读错0的情况。
7.【分析】判断x和y成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例.
【解答】解:因为xy+5=7.5,所以xy=2.5(一定),是x、y的乘积一定,所以x、y成反比例,
故答案为:反.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
8.【分析】有足够的面粉和彩色奶油,要求最多可以做多少个这样的生日蛋糕,根据题意,也就是求8千克里面有几个0.56千克,用除法计算,计算结果要用去尾法取值。
【解答】解:8÷0.56≈14(个)
答:最多可以做14个这种生日蛋糕。
故答案为:14。
【点评】此题主要考查了有余数除法的应用,解答此题的关键是当剩下的白色奶油不够做一个蛋糕时,要舍去,而不能用四舍五入法判断。
二、优化与选择。
9.【分析】“1”平均分成100份,每份表示0.01,因此涂色50个小正方形表示0.50。
【解答】解:阴影部分表示的是0.50。
故选:B。
【点评】此题考查小数的意义和表示方法,要熟练掌握。
10.【分析】根据三角形的内角和为180°,先按照比例分配的方法求出最大角(即3份所对应的角)的度数,再根据最大角的度数即可判断是什么三角形。
【解答】解:180°×=90°
根据直角三角形的含义可知:该三角形是直角三角形。
故选:B。
【点评】依据按比例分配方法,求出最大角的度数,是解答本题的关键。
11.【分析】根据a和b在数轴上的位置可知:a<0,b>0,且a 的绝对值小于b的绝对值。再依次判定四个选项的计算结果情况即可。
【解答】解:根据a和b在数轴上的位置可知:a<0,b>0,且a 的绝对值小于b的绝对值。则:
选项A:a÷b<0。
选项B:a+b>0。
选项C:<0.
选项D:a×(a+b)<0。
故选:B。
【点评】本题考查有理数的运算,根据数轴确定a<0,b>0,且a 的绝对值小于b的绝对值是关键。
12.【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可。
【解答】解:平行四边形不是轴对称图形,正三角形、圆、等腰梯形都是轴对称图形。
故选:A。
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合。
13.【分析】温度高于0℃记作正,则低于0℃就记作负。
【解答】解:某地白天最高温度是零上8℃,记作+8℃,夜间的最低温度比白天最高温度下降了10℃,夜间最低温度记作﹣2℃。
故选:B。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
14.【分析】根据周长是封闭图形一周的长度,数出四个图形的周长为多少格即可解答。
【解答】解:图形①的周长14格,图形②的周长是12格,图形③的周长是12格,图形④的周长是12格。
所以图形①的周长与其它3个图形的周长不同。
故选:A。
【点评】此题主要考查周长的定义,数图形周长为多少格时,是要数图形边线一周的格数。
15.【分析】因为北与东之间的夹角是90°,所以北偏东35°方向,还可以说成东偏北55°;据此选择即可。
【解答】解:北与东之间的夹角是90°,90°﹣35°=55°,
所以文化广场在电视塔的北偏东35°方向,还可以说文化广场在电视塔的东偏北55°方向。
故选:B。
【点评】本题主要考查了方向,解题的关键是明确北与东之间的夹角是90°。
16.【分析】可以直接根据球的数量的多少来判断,数量多的摸到的可能性就大,数量少的摸到的可能性就小.
【解答】解:A和D摸到白球的可能性一样大;
C摸出黑球的可能性最大;
B摸到白球的可能性最大;
故选:B.
【点评】解决此题关键是如果不需要准确地计算可能性的大小时,可以根据各种球个数的多少,直接判断可能性的大小.
17.【分析】圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长等于圆柱底面的周长,宽等于圆柱的高,据此圆柱的底面直径利用周长公式计算出底面周长。
【解答】解:3.14×4=12.56(分米)
圆柱的底面周长是12.56分米,那么长方形的长也是12.56分米。
故选:D。
【点评】此题考查圆柱的侧面展开图,要明确:沿高线剪开,圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高。
18.【分析】等底等高的圆锥的体积是圆柱体积的,把一个圆柱削成一个最大的圆锥,即圆柱和圆锥等底等高,那么削去部分的体积相当于圆柱体积的(1﹣),据此判断。
【解答】解:因为等底等高的圆锥的体积是圆柱体积的,所以削去部分的体积相当于圆柱体积的1﹣=。
故选:C。
【点评】此题解答关键是明确:等底等高的圆锥的体积是圆柱体积的。
19.【分析】根据“甲乙两堆煤的重量比是5:3”把甲堆煤的质量看作5份,乙堆煤的质量看作3份,甲堆的质量比乙堆多(5﹣3)÷3,据此解答即可.
【解答】解:(5﹣3)÷3
=2÷3
=
答:甲比乙多.
故选:C.
【点评】解决此题关键是把比转化为份数,再根据求一个数是另一个数的几分之几的方法进行解答.
20.【分析】根据正方体展开图的11种特征,图A、图B和图C都不属于正方体展开图,不能按虚线折成一个正方体;图D属于正方体展开图的“2﹣2﹣2”结构,能按虚线折成一个正方体。
【解答】解:能按虚线折成一个正方体。
故选:D。
【点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
21.【分析】500分=6时20分。
每天24小时,500小时≈21(天)。
一年约52周,500周≈10年。
每年12个月,500月≈42年,和王老师的年龄相差太多。
【解答】解:王老师今年42岁了,上面500月接近王老师今年的年龄。
故选:D。
【点评】解答此题的关键是把小时数、天数、周数、月数都估算成年数,然后再根据王老师的年龄进行选择。
22.【分析】此题通过分析已知条件,设若甲数÷0.99=乙数×0.99=1,得出甲、乙两个具体的数,就很好比较了.
【解答】解:设甲数÷0.99=乙数×0.99=1,
那么甲数=0.99×1=0.99,
乙数=1÷0.99≈1.01,
因为0.99<1.01,所甲数<乙数;
故选:B.
【点评】此题考查了学生对小数大小比较方法的掌握情况,以及分析能力.
23.【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,把一个圆柱形木块切削成一个和它等底等高的圆锥模型。圆锥的体积是圆柱体积的。据此解答。
【解答】解:把一个圆柱形木块切削成一个和它等底等高的圆锥模型。圆锥的体积是圆柱体积的。
故选:A。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
24.【分析】根据平行四边形、长方形、正方形的特征,平行四边形的对边平行且相等,长方形的对边相等;正方形的4条边的长度都相等,所以长方形和正方形是特殊的平行四边形.据此解答即可.
【解答】解:平行四边形包括长方形和正方形,
所以
故选:A.
【点评】此题考查的目的是理解掌握平行四边形、长方形、正方形的特征以及它们之间的关系.
25.【分析】先用剩下的米数除以剩下米数占甲全长的几分之几,求出甲的全长,用剩下的米数加上乙剪去的米数求出乙的全长,再比较。
【解答】解:÷(1﹣)
=÷
=(米)
+=(米)
米<米
答:原来的两根彩带,乙比甲长。
故选:B。
【点评】此题主要考查分率与数量的区别,解答时需要掌握分数问题中求标准量的方法。
26.【分析】根据镜面对称的特征,镜中的景物与实际景物上下前后方向一致,左右方向相反,大小不变,且关于镜面对称。
【解答】解:它的“倒影”应是。
故选:D。
【点评】此题主要明白镜面对称的特点是:上下前后方向一致,左右方向相反,镜中与实际景物大小不变。
27.【分析】先求出糖水的克数,再用糖的克数除以糖水的克数即可求解。
【解答】解:10÷(10+100)
=10÷110
=
答:糖占糖水的。
故选:B。
【点评】解题的关键是明确糖水的克数=糖的克数+水的克数。
28.【分析】在对折好的纸上剪1个□,打开后会有2个□,以折线成对称图形。一个在左上角,一个在右上角。剪半个☆,展开后就是一个☆,据此逐项分析即可解答。
【解答】解:在对折好的纸上剪两个洞,打开后的图形是。
故选:D。
【点评】本题考查轴对称图形的辨识,结合题意分析解答即可。
三、运算与求值。
29.【分析】根据等式的性质,方程两边同时减去10,然后再同时除以12.5%求解;
先化简,然后再根据等式的性质,方程两边同时除以求解;
根据等式的性质,方程两边同时加上,然后再同时除以求解。
【解答】解:12.5%x+10=18
12.5%x+10﹣10=18﹣10
12.5%x=8
12.5%x÷12.5%=8÷12.5%
x=64
x=13
x=13
x÷=13÷
x=21
x﹣+=+
x=
x÷=÷
x=
【点评】此题考查了运用等式的性质解方程,即等式两边同加上或同减去、同乘上或同除以一个数(0除外),两边仍相等,同时注意“=”上下要对齐。
30.【分析】(1)根据乘法分配律简算;
(2)先算小括号里面的减法,再算括号外的除法,最后算括号外的乘法;
(3)先算小括号里面的加法,再算中括号里面的除法,最后算括号外的除法。
【解答】解:(1)4.9×6.4+15.1×6.4
=(4.9+15.1)×6.4
=20×6.4
=128
(2)(826﹣370)÷38×6
=456÷38×6
=12×6
=72
(3)19÷[(+)÷]
=19÷[÷]
=19÷
=10
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
31.【分析】(1)按照从左到右的顺序计算;
(2)(3)先把除法变成乘法,然后约分求解。
【解答】解:(1)××
=×
=
(2)×÷
=××
=
(3)÷14÷
=××
=
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
32.【分析】估算,一般要根据“四舍五入”法把数看作是整十、整百、整千…的数来进行计算,据此解答.
【解答】解:896+309≈900+300=1200
723÷89≈720÷90=8
【点评】此题考查了加法和除法估算方法的运用.
四、调查与统计。
33.【分析】根据统计表可知各种级别的城市占占监测城市的百分之几,所以用扇形统计图比较合适;
(1)先根据达到二级(含二级)标准以上占城市总数的65.8%,它对应的数量是344个,由此用除法求出监测城市的总数,然后用监测城市的总数乘25.4%即可求出达到三级标准以上的城市数;再用1减去65.8%,再减去25.4%即可求出未到三级标准的城市数占的百分数.
(2)比较三种类型城市占的百分数,百分数大的扇形的面积就大,由此补充完整扇形统计图.
【解答】解:该情况选用 扇形统计图表示比较合适.
344÷65.8%≈523(个)
523﹣344﹣46=133(个)
1﹣65.8%﹣25.4%
=34.2%﹣25.4%
=8.8%
所以统计表如下:
空气质量情况 | 城市个数 | 占监测城市的百分之几(百分号前保留一位小数) |
达到二级(含二级)标准以上 | 344 | 65.8% |
达到三级标准 | 133 | 25.4% |
未达到三级标准 | 46 | 8.8% |
扇形统计图如下:
【点评】找清楚单位“1”,抓住扇形统计图的绘制特点,是解决本题的关键.
五、判断与说理。
34.【分析】(1)把捐款总数看作单位“1”,根据求一个数的百分之几是多少,用乘法解答。
(2)从这幅图中不能得出“五年级学生捐款数最多”的结论,理由是一、二年级共捐款占全校捐款总数的35%,这里一年级或二年级捐款数量可能比五年级多。
【解答】解:(1)4万=40000
40000×15%=6000 (元)
答:四年级学生捐款6000元。
(2)不能,理由是一、二年级共捐款占全校捐款总数的35%,这里一年级或二年级捐款数量可能比五年级多。
【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
35.【分析】根据长方形的面积=长×宽,把数据代入公式求出整块菜地面积再除以2就是白菜地的面积,用整块菜地面积的一半除以2就是萝卜地的面积。据此解答。
【解答】解:32×15=480(平方米)
480÷2=240(平方米)
240÷2=120(平方米)
答:白菜地的面积是240平方米,萝卜地的面积是120平方米。
【点评】此题主要考查长方形面积公式的灵活应用,关键是熟记公式。
六、情境与应用。
36.【分析】先推算出火车行驶的时间,再计算出速度差,最后根据速度=路程÷时间,就可以计算出汽车每小时行驶多少千米。
【解答】解:9时﹣7时=2时
(500﹣300)÷2
=200÷2
=100(千米)
答:汽车每小时行驶100千米。
【点评】本题考查行程问题的解题方法,解题关键是先推算出火车行驶的时间,再根据行程问题的数量关系,利用速度=路程÷时间,列式计算。
37.【分析】由图知:将梯形分成底a和底b、高为h的两个三角形,通过“旋转”或“割补”法,把两个三角形拼成一个大三角形,这个大三角形的底是(a+b),高是h,拼成的大三角形的底等于梯形的上下底之和,拼成的三角形的高等于梯形的高,虽然形状变了。但是面积不变,根据三角形的面积公式:S=ah÷2,推导出梯形的面积公式。据此解答。
【解答】解:把这个梯形分成底a和底b、高为h的两个三角形,通过“旋转”或“割补”法,把两个三角形拼成一个大三角形,这个大三角形的底是(a+b),高是h,拼成的大三角形的底等于梯形的上下底之和,拼成的三角形的高等于梯形的高,虽然形状变了。但是面积不变,根据三角形的面积公式:S=ah÷2,推导出梯形的面积公式:S=(a+b)h÷2。
【点评】此题考查的目的是理解掌握梯形面积公式的推导过程及应用,掌握三角形面积计算方法,把梯形转化为两个三角形,进而推导出梯形面积公式。
38.【分析】要想节省时间,能同时做的事尽量同时去做,把锅烧热需要2分钟,在等锅热的时间可以同时洗鱼;把油烧热需要3分钟,在等油烧热的时间可以同时切鱼、切姜片.
【解答】解:根据分析可知:
设计一个巧妙合理的新顺序如图:
【点评】此题属于合理安排时间问题,要奔着既节约时间又不使每道工序相矛盾进行解答.
39.【分析】(1)通过观察图形可知,60秒后水箱注满了水,此时应该关闭水龙头。
(2)根据乘法的意义,用每秒注水的体积乘注水的时间即可。
(3)通过观察统计图可知,当注水高度达到A点时用了45秒,求出45秒注水的体积,根据长方体的体积公式:V=Sh,那么h=V÷S,把数据代入公式求出45秒注水的高度,45秒注水的高度是水箱高度的一半,据此可以求出水箱的高。
【解答】解:(1)由图可知,60秒后水箱注满了水,此时应该关闭水龙头。
(2)0.1×60=6(升)
答:这个水箱的容积是6升。
(3)0.1×45=4.5(升)
4.5升=4.5立方分米
4.5÷(3×2)×2
=4.5÷6×2
=0.75×2
=1.5(分米)
答:这个水箱的高度是1.5分米。
故答案为:60;6。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,长方体的体积(容积)公式及应用,关键是熟记公式。
40.【分析】(1)根据公式,标准体重计算方法是:标准体重kg=(身高cm﹣80)×70%,代入数值进行计算即可;
(2)用李平的体重与标准体重相减的差除以标准体重再乘100%,就可知道李平的体重在哪个范围之内;
(3)根据李平的体重在哪个范围之内,找出合理的建议即可。(答案不唯一)
【解答】解:(1)(150﹣80)×70%
=70×70%
=49(kg)
答:李平同学的标准体重应该是49kg。
(2)(60﹣49)÷49×100%
=11÷49×100%
≈0.224×100%
=22.4%
答:22.4%在超出标准题中20%~30%的范围内,属于轻度肥胖。
(3)李平的体重属于轻度肥胖,我建议平时要加强锻炼,饮食要均衡,不能暴饮暴食,争取达到标准体重。(答案不唯一)
【点评】本题考查了百分数的实际应用,根据题中所给的数量关系,先求出李平的标准体重,再进一步解答即可。
2023年江苏省连云港市灌南县小升初数学试卷: 这是一份2023年江苏省连云港市灌南县小升初数学试卷,共24页。试卷主要包含了理解与填空,优化与选择,运算与求值,情境与运用等内容,欢迎下载使用。
2022年江苏省连云港市灌南县小升初数学试卷: 这是一份2022年江苏省连云港市灌南县小升初数学试卷,共22页。
2022年江苏省连云港市灌南县小升初数学试卷: 这是一份2022年江苏省连云港市灌南县小升初数学试卷,共22页。













