专题09《比的认识》 ——2022-2023学年小学数学六年级下册小升初全国通用版专题复习讲义（原卷版+解析版）

这是一份专题09《比的认识》 ——2022-2023学年小学数学六年级下册小升初全国通用版专题复习讲义（原卷版+解析版），文件包含专题09《比的认识》2022-2023学年小学数学六年级下册小升初全国通用版专题复习讲义解析版docx、专题09《比的认识》2022-2023学年小学数学六年级下册小升初全国通用版专题复习讲义原卷版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。
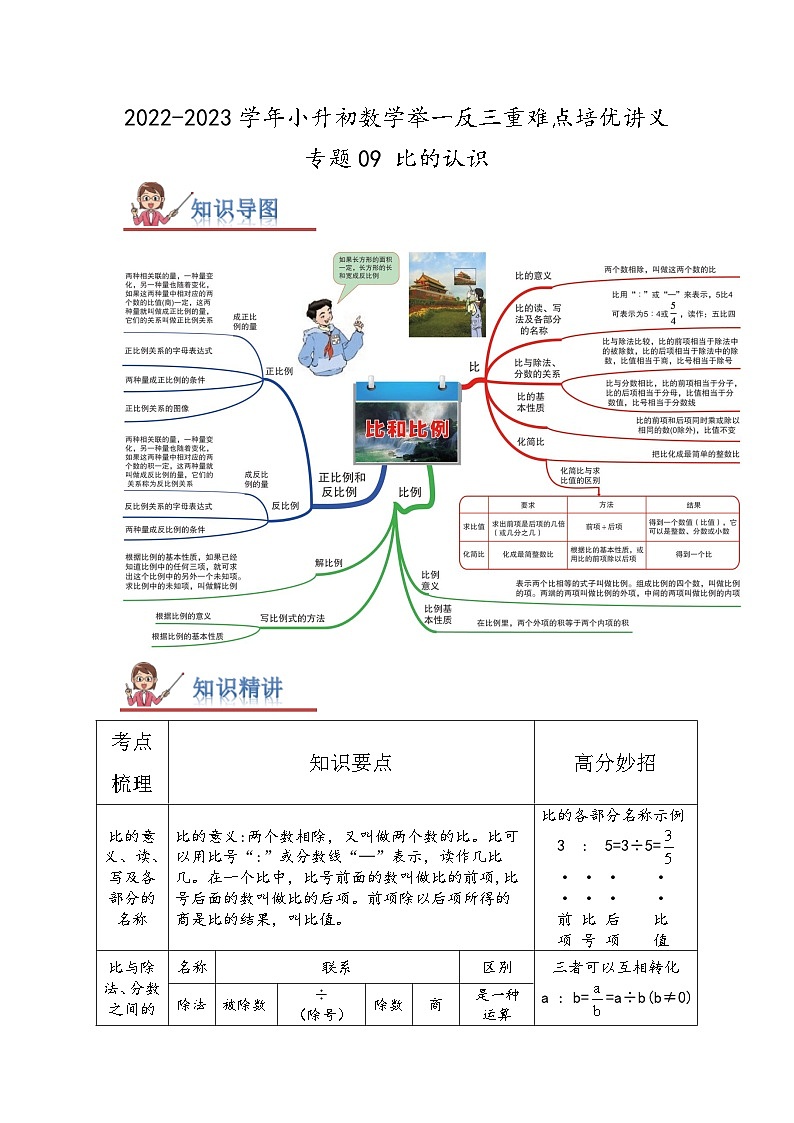
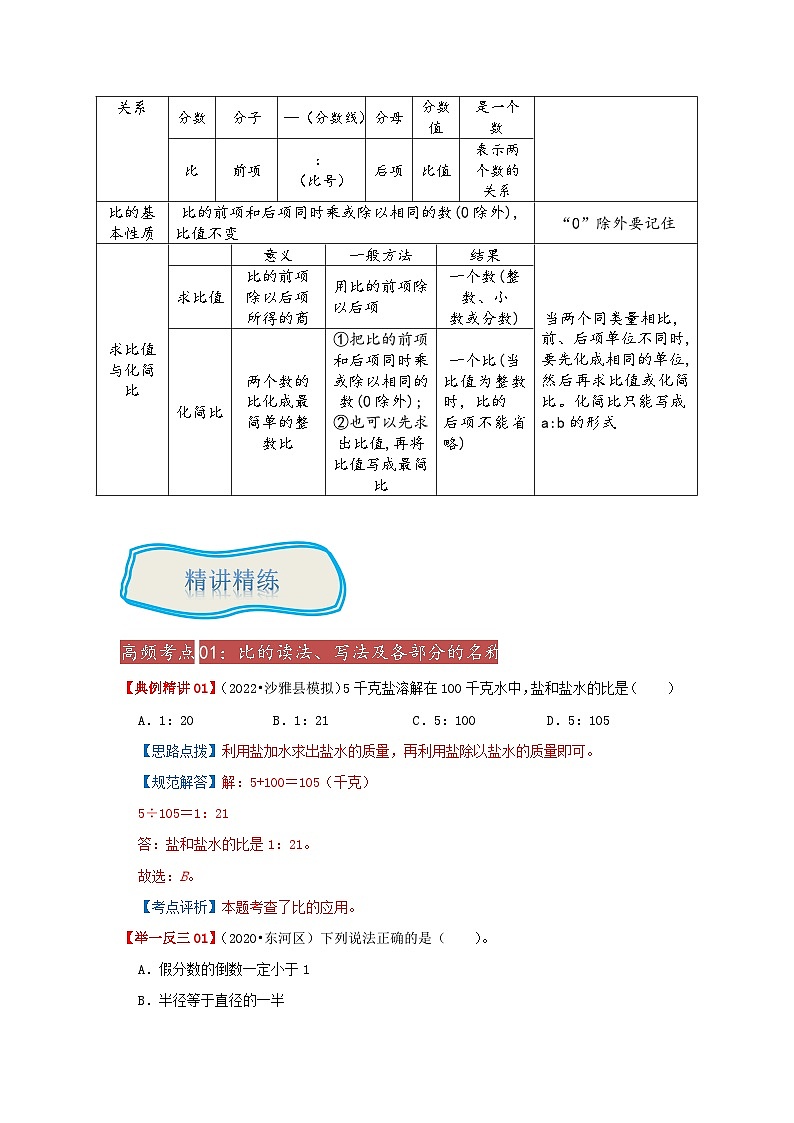
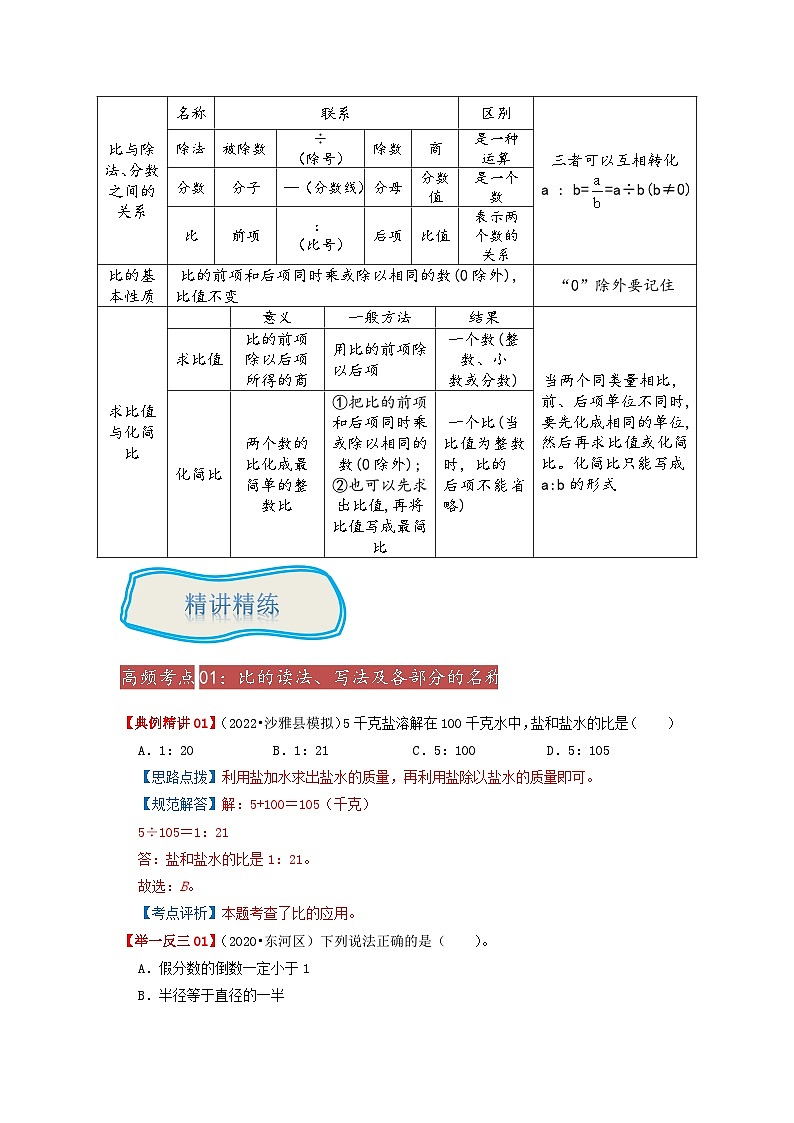
2022-2023学年小升初数学举一反三重难点培优讲义专题09 比的认识考点梳理知识要点高分妙招比的意义、读、写及各部分的名称比的意义:两个数相除，又叫做两个数的比。比可以用比号“:”或分数线“—”表示，读作几比几。在一个比中，比号前面的数叫做比的前项,比号后面的数叫做比的后项。前项除以后项所得的商是比的结果，叫比值。比的各部分名称示例3  :  5=3÷5=· · ·    ·· · ·    ·前 比 后    比项 号 项    值比与除法、分数之间的关系名称联系区别三者可以互相转化a : b==a÷b(b≠0)除法被除数÷（除号）除数商是一种运算分数分子—（分数线）分母分数值是一个数比前项：（比号）后项比值表示两个数的关系比的基本性质比的前项和后项同时乘或除以相同的数(0除外),比值不变“0”除外要记住求比值与化简比 意义一般方法结果当两个同类量相比，前、后项单位不同时,要先化成相同的单位,然后再求比值或化简比。化简比只能写成a:b的形式求比值比的前项除以后项所得的商用比的前项除以后项一个数(整数、小数或分数)化简比两个数的比化成最简单的整数比①把比的前项和后项同时乘或除以相同的数(0除外);②也可以先求出比值,再将比值写成最简比一个比(当比值为整数时，比的后项不能省略) 高频考点01：比的读法、写法及各部分的名称【典例精讲01】（2022•沙雅县模拟）5千克盐溶解在100千克水中，盐和盐水的比是（　　）A．1：20 B．1：21 C．5：100 D．5：105【思路点拨】利用盐加水求出盐水的质量，再利用盐除以盐水的质量即可。【规范解答】解：5+100＝105（千克）5÷105＝1：21答：盐和盐水的比是1：21。故选：B。【考点评析】本题考查了比的应用。【举一反三01】（2020•东河区）下列说法正确的是（　　）。A．假分数的倒数一定小于1 B．半径等于直径的一半 C．半径的长短决定圆的大小 D．校篮球队决赛比分是1：0，所以比的后项可以是0【思路点拨】A：假分数：是指分子大于或等于分母的分数；再根据乘积是1的两个数互为倒数，用1除以一个假分数就得一个真分数或得1，这个分数是小于或等于1；所以本选项说法错误；B：在同一个圆或等圆内，直径的长度都是半径长度的2倍，半径的长度是直径的一半，所以半径等于直径的一半，所以本选项说法错误；C：连接圆心和圆上任意一点的线段叫半径．根据圆心决定圆的位置，半径决定圆的大小；所以本选项说法正确；D：比的意义是：两个数相除，又叫做两个数的比，比的后项不能为零；某次比赛甲队和乙队的比分是1：0，这里表示两个队比赛的情况，0表示没有，它不是数学中的比，所以某次比赛甲队和乙队的比分是1：0，所以比的后项可以是0，所以本选项说法错误。【规范解答】解：根据分析可得：说法正确的是：半径的长短决定圆的大小。故选：C。【考点评析】此题考查的知识点较多，仔细审题是解题的关键。【举一反三02】（2019•长沙模拟）一个比的比值是1，后项是2.5，前项是（　　）A．2.5 B．1.5 C．2【思路点拨】因为，前项÷后项＝比值，根据乘法与除法之间的联系，比的前项相当于除法中的被除数，后项相当于除数，比值相当于商，因为被除数＝除数×商，所以前项＝后项×比值，据此解答．【规范解答】解：2.5×1＝2.5，答：前项是2.5．故选：A．【考点评析】此题考查的目的是理解掌握比的意义，比与除法之间的联系及应用．【举一反三03】（2021•锡山区）　16　÷20＝4：5＝＝　80　%【思路点拨】根据比与分数的关系4：5＝＝，再根据商不变的性质被除数、除数都4就是16÷20，化成百分数就是80%，由此填空即可。【规范解答】解：16÷20＝4：5＝＝80%故答案为：16，15，80。【考点评析】此题主要是考查除法、小数、分数、比之间的关系及转化．利用它们之间的关系和性质进行转化即可。高频考点02：比与分数、除法的关系【典例精讲02】（2023•铁山区模拟）9÷　12　＝　15　：20＝　3　÷　4　＝0.75＝　75　%。【思路点拨】把0.75化成分数并化简是，根据分数与除法的关系，＝3÷4；再根据商不变的性质被除数、除数都乘3就是9÷12；根据比与分数的关系，＝3：4，再根据比的基本性质比的前、后项都乘5就是15：20；把0.75的小数点向右移动两位添上百分号就是75%。【规范解答】解：9÷12＝15：20＝3÷4＝0.75＝75%。故答案为：12，15，3，4，75。【考点评析】此题主要是考查除法、小数、分数、百分数、比之间的关系及转化。利用它们之间的关系和性质进行转化即可。【举一反三04】（2022秋•蕉岭县期末）12÷　60　＝0.2＝　1　：　5　＝＝　20　%【思路点拨】解决此题关键在于0.2，0.2可化成分数，的分子和分母同时乘2可化成；的分子和分母也可以同时除以2可化成最简分数，用分子1做被除数，分母5做除数可转化成除法算式1÷5，1÷5的被除数和除数同时乘上12可化成12÷60；也可用分子1做比的前项，分母5做比的后项转化成比1：5；0.2的小数点向右移动两位，同时添上百分号可化成20%；由此进行转化并填空．【规范解答】解：12÷60＝0.2＝1：5＝＝20%；故答案为：60，1，5，4，20．【考点评析】此题考查小数、分数、百分数、比和除法之间的转化，利用它们之间的关系和性质进行转化．【举一反三05】（2022•建华区）＝16：　20　＝　80　%＝　100　÷125＝　0.8　（填小数）。【思路点拨】根据比与分数的关系＝4：5，再根据比的基本性质比的前、后项都乘4就是16：20；根据分数与除法的关系＝4÷5，再根据商不变的性质被除数、除数都乘25就是100÷125；4÷5＝0.8；把0.8的小数点向右移动两位，添上百分号就是80%。【规范解答】解：＝16：20＝80%＝100÷125＝0.8故答案为：20，80，100，0.8。【考点评析】此题主要是考查小数、分数、除法、比、百分数之间的关系及转化。利用它们之间的关系和性质进行转化即可。【举一反三06】（2023•硚口区模拟）6÷　8　＝　9　：12＝＝　75　%＝0.75【思路点拨】把0.75化成分数并化简是，根据分数与除法的关系＝3÷4，再根据商不变的性质被除数、除数都乘2就是6÷8；根据比与分数的关系＝3：4，再根据比的基本性质比的前、后项都乘3就是9：12；根据分数的基本性质的分子、分母都乘5就是；把0.75的小数点向右移动两位添上百分号就是75%。【规范解答】解：6÷8＝9：12＝＝75%＝0.75故答案为：8，9，15，75。【考点评析】此题主要是考查小数、分数、除法、比、百分数之间的关系及转化。利用它们之间的关系和性质进行转化即可。高频考点03：比的性质【典例精讲03】（2021•隆阳区）把5：3的后项加上9，要使比值不变，前项应（　　）A．加上9 B．扩 大到原来的4倍 C．扩大到原来的9倍【思路点拨】比的前项和后项同时乘或除以相同的数（0除外），比值不变。【规范解答】解：把5：3的后项加上9，即3+9＝12，12÷3＝4，相当于后项扩大到原来的4倍，要使比值不变，前项也扩大到原来的4倍。故选：B。【考点评析】熟练掌握比的基本性质是解题的关键。【举一反三07】（2021•汝城县）把3：5的后项加上15，要使这个比的比值不变，前项要乘 　4　。【思路点拨】根据比的基本性质，比的前项和后项同时乘或除以相同的数（0除外），比值不变。首先观察后项的变化，后项5+15＝20，也就是后项乘4，要使比值不变，前项要乘4。据此解答。【规范解答】解：5+15＝18，20＝5×4要使比值不变，前项要乘4。即3×4＝12答：前项要乘4。故答案为：4。【考点评析】此题考查的目的是理解掌握比的基本性质及应用。【举一反三08】（2019•长沙模拟）比的前项扩大3倍，后项扩大2倍，比值则扩大6倍．　×　．（判断对错）【思路点拨】根据比的性质，可知比的前项扩大3倍，后项扩大2倍，比值则扩大倍；可以通过举例子进行验证．【规范解答】解：例如：4：1，比值是：4：1＝4÷1＝4，比的前项扩大3倍，由4变成12，后项扩大2倍，由1变成2，比变成12：2，比值是：12：2＝12÷2＝6，比值由4变成6，是扩大了：6÷4＝．故判断为：错误．【考点评析】此题考查比的性质的运用：比的前项扩大3倍，后项扩大2倍，比值则扩大倍．【举一反三09】（2022秋•铁门关市期末）把一个比的前项扩大到原来的3倍，后项缩小到原来的，它的比值不变． 　×　（判断对错）【思路点拨】依据比的性质，即比的前项和后同时乘或除以一个不等于零的数，比的大小不变，若比的前项扩大3倍，后项缩小3倍，就相当于比值扩大了（3×3）倍，据此即可做出判断．【规范解答】解：若比的前项扩大3倍，后项缩小3倍，比值扩大3×3＝9倍；例如：，的前项扩大3倍，后项缩小3倍，比值为，÷＝9；故答案为：×．【考点评析】解答此题的主要依据是：比的基本性质，解答时可以举例说明．高频考点04：求比值和化简比【典例精讲04】（2023•樊城区模拟）把0.4cm：m化简成最简整数比是 　1：50　；如果把它的前项加9，那么后项 　乘10　，才使它的比值不变。【思路点拨】先统一单位，再根据比的基本性质，即比的前项和后项同时乘或除以一个相同的数（0除外）比值不变，进而把比化成最简比；把化简后的前项加9，根据比的基本性质得出前项相当于乘几，要使比值不变，后项也得乘几。【规范解答】解：0.4cm：m＝0.4cm：20cm＝0.4：20＝（0.4÷0.4）：（20÷0.4）＝1：501：50前项加9，前项变为1+9＝10，前项相当于乘10，要使比值不变，后项也得乘10。故答案为：1：50；乘10。【考点评析】本题主要考查了比的性质及化简比，要注意化简比的结果仍然是一个比，它的前项和后项都是整数，并且互质。【举一反三10】（2022•交口县）吨：25千克＝　20　（比值）1.25：2＝　5：8　（化简比）24分＝　　时4升50毫升＝　4050　毫升【思路点拨】先统一单位单位，再根据比的基本性质，即比的前项和后项同时乘一个数或除以一个数（0除外）比值不变；根据求比值的方法，用比的前项除以后项即可。【规范解答】解：吨：25千克＝500千克÷25千克＝20 1.25：2＝（1.25×4）：（2×4）＝5：8 24分＝时4升50毫升＝4050毫升吨：25千克＝20（比值）1.25：2＝5：8（化简比）24分＝时4升50毫升＝4050毫升故答案为：20；5：8；；4050。【考点评析】本题主要考查了求比值和化简比、单位换算的应用。【举一反三11】（2022•平桥区）如图，四个相同的直角三角形围成一个正方形，已知a＝3b，则阴影部分与整个图形的面积关系分别用最简比、百分数表示是 　5　：　8　＝　62.5　%。【思路点拨】分别求出大正方形和阴影部分的面积，再求两个面积比，最后将比值化成百分数。【规范解答】解：由a＝3b大正方形的面积：（a+b）2＝（3b+b）2＝16b24个三角形的面积和：4×ab＝4×（×3b×b）＝6b2阴影部分面积：16b2﹣6b2＝10b2所以阴影部分与整个图形的面积比为：10b2：16b2＝5：85：8＝5÷8＝0.625＝62.5%故答案为：5，8，62.5。【考点评析】本题考查了比的化简和用字母表示数，关键是如何用字母b表示大正方形及阴影部分的面积。【举一反三12】（2023•滨州模拟）最简比的前项和后项一定是互质数。　√　（判断对错）【思路点拨】化简比利用比的性质进行，最简比的前项和后项只有公约数1，则最简比的前项和后项一定是互质数。【规范解答】解：经分析可知：最简比的前项和后项一定是互质数。故题干说法正确。故答案为：√。【考点评析】本题考查求比值和化简比。高频考点05：比的应用【典例精讲05】（2022•红安县）人们的肚脐是人体总长的黄金分割点（由脚底至肚脐的长度与身高之比为0.618），则肚脐到脚底的距离/身高＝0.618才是最完美的身材比例。近代有很多女性喜欢穿高跟鞋以增加下身长度，使自己的身材显得婀娜，那么如何利用黄金分割计算赵女士所需要的高跟鞋高度；赵女士身高165，肚脐到脚底长度是100cm；请利用黄金分割计算赵女士所需要的高跟鞋高度约是（　　）cm较好。A．6 B．8 C．10 D．12【思路点拨】根据“当人体的躯干与身高的比例是0.618：1时，这个人的身材比例就越完美，”即要使人的身材最优美，人体的躯干与身高的比值是一定的，由此列出比例，解决问题。【规范解答】解：她应选择x厘米的高跟鞋。（100+x）：（165+x）＝0.618：1       （165+x）×0.618＝100+x            101.97+0.618x＝100+x                        0.382x＝1.97                              x≈6答：她应选6厘米的高跟鞋。故选：A。【考点评析】解答此题的关键是，穿上高跟鞋时，身高和下肢的长度都发生变化，由此得出对应的下肢的长度与身高，再根据下肢与身高的比值一定，列出比例解决问题。【举一反三13】（2022•源汇区）一种药水是用药粉和水按1：200配制成的，现有药粉12千克，需要加水 　2400　千克，配制成了药水是 　2412　千克。【思路点拨】药粉和水的比是1：200，即水的质量是药粉的200倍，所以用药粉乘200求出需要加的水，再用水+药粉就等于药水。【规范解答】解：12×200＝2400（千克）2400+12＝2412（千克）答：需要加水2400千克，配制成了药水是2412千克。故答案为：2400，2412。【考点评析】本题考查了比的问题，关键是根据比的意义先求出水。【举一反三14】（2022•鄞州区）一个等腰三角形的底与高长度之比是10：3，如果沿这个三角形的对称轴剪开，可以拼成一个周长是48cm的长方形。原来这个三角形的面积是 　135　cm2【思路点拨】因为沿这个等腰三角形的对称轴剪开，可以拼成一个周长是48cm的长方形，这个时候长方形的周长就是原来等腰三角形的底加两条高的长度；而底与高长度之比是10：3，那么底与两条高的长度之比是10：（2×3）＝10：6＝5：3，然后根据按比例分配的方法求出底和两条高的长度，从而求出高，最后求出三角形的面积。【规范解答】解：10：（2×3）＝10：6＝5：3  48÷（5+3）＝48÷8＝6（cm）底：6×5＝30（cm）高：6×3÷2＝9（cm）面积：30×9÷2＝135（cm2）故答案为：135。【考点评析】此题需要学生熟悉等腰三角形的特点，并掌握三角形的面积公式，还需会用按比分配的方法解决问题。【举一反三15】．（2023•硚口区模拟）你能根据明明和芳芳的对话求出三种果树的面积分别是多少平方米吗？【思路点拨】将果园面积看作单位“1”，先用4000乘37.5%，求出栽苹果树的面积；然后用4000平方米减去栽苹果树的面积，求出剩下的面积；最后根据按比例分配的方法求出栽桃树和梨树的面积即可。【规范解答】解：4000×37.5%＝1500（平方米）4000﹣1500＝2500（平方米）2500×＝500（平方米）2500×＝2000（平方米）答：栽苹果树的面积为1500平方米，栽桃树的面积为500平方米，栽梨树的面积为2000平方米。【考点评析】本题考查了利用百分数乘法和按比例分配解决问题，需准确分析题目中的数量关系。一．选择题1．（2022•未央区）一个圆柱和一个圆锥底面半径的比是2：3，圆锥的高是圆柱的2倍，则圆柱和圆锥的体积比是（　　）A．2：3 B．3：2 C．4：3【思路点拨】设圆柱的底面半径为2，圆锥的底面半径为3，圆柱的高是1，圆锥的高是2，利用赋值法解答。【规范解答】解：设圆柱的底面半径为2，圆锥的底面半径为3，圆柱的高是1，圆锥的高是2。π×22×1＝4π×π×32×2＝6π4π：6π＝2：3故选：A。【考点评析】解答此类问题用赋值法比较简便。2．（2022•北辰区）一项工程，甲单独做需要小时，乙单独做需要0.25小时，甲、乙两人的工作效率的比是（　　）A．16：5 B．5：16 C．5：1 D．1：5【思路点拨】根据工作量÷工作时间＝工作效率，分别求出二人的工作效率，再求工作效率比。【规范解答】解：1÷＝1÷0.25＝4：4＝（×4）：（4×4）＝5：16故选：B。【考点评析】解答本题需熟练掌握工作量、工作时间和工作效率的关系，并能利用比的基本性质化简比。3．（2022•房山区模拟）一项工程，甲队单独做要8天完成，乙队单独做要10天完成。甲乙两队工作效率的最简比是（　　）A．： B．： C．5：4 D．4：5【思路点拨】把工作总量看成是单位“1”，然后分别求出甲、乙的工作效率，然后写出效率比并化简。【规范解答】解：甲的效率：1÷8＝；乙的效率：1÷10＝；甲乙两队工作效率比为：：＝（×40）：（×40）＝5：4。故选：C。【考点评析】本题考查了比的意义和化简，时间分之一可以看作效率。4．（2022•黄岩区）走同一条路，小刚用了小时，小明用了小时，则小明与小刚的平均速度之比是（　　）A．5：6 B．6：5 C． D．【思路点拨】把这条路的路程看作单位“1”，根据平均速度＝路程÷时间，写出小明与小刚的平均速度之比，再化简即可。【规范解答】解：（1÷）：（1÷）＝：3＝（×2）：（3×2）＝5：6答：小明与小刚的平均速度之比是5：6。故选：A。【考点评析】本题主要考查了比的意义及简单的行程问题，解题的关键是掌握平均速度＝路程÷时间。二．填空题（5．（2023•硚口区模拟）某小学本学期参加延时服务的同学比不参加延时服务的同学多25%，参加延时服务的同学与全校同学的比是 　5：9　。【思路点拨】把不参加延时服务的同学人数看作单位“1”，则参加延时服务的同学人数为（1+25%），全校同学人数为（1+1+25%），然后求出参加延时服务的同学人数与全校同学人数的比即可。【规范解答】解：（1+25%）：（1+1+25%）＝1.25：2.25＝5：9答：参加延时服务的同学与全校同学的比是5：9。故答案为：5：9。【考点评析】此题的解题关键是找准题目中的单位“1”，用百分数表示出两个部分的人数占比，即可得出结果。6．（2022秋•菏泽期末）两个圆的半径比是3：4，它们的周长比是　3：4　，面积比是　16：9　．【思路点拨】设大圆的半径为R，小圆的半径为r，根据“圆的周长＝2πr”分别求出大圆和小圆的周长，进而求比即可；根据“圆的面积＝πr2”分别求出大圆的面积和小圆的面积，进而根据题意求比即可．【规范解答】解：设大圆的半径为R，小圆的半径为r，2πR：2πr＝（2πR÷2π）：（2πr÷2π）＝R：r＝4：3； πR2：πr2＝（πR2÷π）：（πr2÷π）＝R2：r2＝42：32＝16：9；答：大圆周长和小圆周长的比是4：3，大圆和小圆的面积比是16：9．故答案为：3：4，9：16．【考点评析】解答此题应明确：两个圆的半径比，即周长的比，面积比是半径的平方的比；用到的知识点：（1）比的意义；（2）圆的周长计算方法；（3）圆的面积计算方法．7．（2022•樊城区）0.5：4.5的比值是 　　，如果前项加上1.5，要使比值不变，后项应该加上 　13.5　。【思路点拨】用比的前项除以后项即可求出比值；如果前项加上1.5，扩大到原来的4倍，后项也要扩大到原来的4倍。据此解答。【规范解答】解：0.5：4.5＝0.5÷4.5＝（0.5+1.5）÷0.5＝44.5×4﹣4.5＝13.5故答案为：，13.5。【考点评析】此题考查了求比值份方法及比的基本性质的运用，比的前项和后项同时乘或除以相同的数（0除外），比值不变。8．（2022•房山区模拟）在德国心理学家费希纳做的“长方形选美”实验中，发现当宽与长的比值约是0.618时，这个长方形最美。因此，比值是0.618的比被称作“黄金比”。请举一个符合黄金比的生活实例 　电视屏幕　。【思路点拨】根据黄金比的了解和生活经验填空即可。【规范解答】解：符合黄金比的生活实例有电视屏幕、写字台面、书籍、衣服、门窗等。故答案为：电视屏幕。（答案不唯一）【考点评析】本题考查了比，两数相除又叫两个数的比。9．（2022•邓州市）如图（单位：cm），在长方形中，甲、乙、丙三个图形面积的比是 　1：5：4　。【思路点拨】三个图形的高相等，依据各自的面积公式即可推出结果．【规范解答】解：设甲、乙、丙的高为h，三角形的面积：2×h÷2＝h平行四边形的面积：5×h＝5h梯形的面积：[3+（3+5+2﹣5）]×h÷2＝[3+5]×h÷2＝4h由此可以得出它们的面积比是：h：5h：4h＝1：5：4。故答案为：1：5：4。【考点评析】此题主要考查等高的图形面积大小，利用公式即可以推算。10．（2018•海门市校级模拟）把10千克盐溶入190千克水中，盐和水的质量比是　1：19　，这被盐水的含盐率是　5%　．【思路点拨】依据比的意义，用盐的质量比水的质量，即可求出盐和水的比；用盐的质量除以盐水的质量，再乘上100%，就是含盐率，据此解答即可．【规范解答】解：10：190＝1：19； 10÷（10+190）×100%＝10÷200×100%＝5%；答：盐和水的质量比是1：19，盐水的含盐率是5%．故答案为：1：19；5%．【考点评析】此题主要考查比的意义的灵活应用，以及含盐率的计算方法．三．判断题11．（2022•丹棱县）把甲班人数的调入乙班后，两班人数相等，原来甲、乙两班人数的比是3：2．　√　．（判断对错）【思路点拨】把甲班人数的调入乙班后，两班人数相等，说明甲班人数比乙班人数多甲班人数的（×2），把甲班人数看作单位“1”，则乙班人数是甲班人数的（1﹣×2），进而根据题意，进行比即可．【规范解答】解：1：（1﹣×2）＝1：＝（1×3）：（×3）＝3：2；答：原来甲、乙两班人数比是3：2．故答案为：√．【考点评析】解答此题的关键：判断出单位“1”，转化为同一单位“1”下进行比，然后化为最简整数比即可．12．（2022•鹤城区）打同一篇稿件，小强用了10分钟，小玲用了12分钟，小强和小玲的打字速度之比是6：5．　√　．（判断对错）【思路点拨】小强与小玲打字的速度比，即工作效率的比，把工作总量看作单位“1”，根据“工作总量÷工作时间＝工作效率”分别求出小强和小玲的工作效率，进而根据题意，进行比即可．【规范解答】解：（1÷10）：（1÷12）＝＝6：5故答案为：√．【考点评析】解答此题用到的知识点：（1）比的意义；（2）工作总量、工作效率和工作时间三者之间的关系．13．（2021•瑞金市）百米赛跑，小强用时18秒，小飞用时15秒，小强与小飞的速度比是6：5。 　×　（判断对错）【思路点拨】根据速度＝路程÷时间分别求出二人的速度，再求速度比并化成最简整数比。【规范解答】解：100÷18＝100÷15＝：＝15：18＝5：6原题说法错误。故答案为：×。【考点评析】解答本题还可以将100米看做单位“1”，分别求出二人的速度，再求速度比并化成最简整数比。四．计算题14．（2019•翔安区）化简比．8：360.25：0.5：．【思路点拨】根据比的基本性质，即比的前项和后项同时乘或除以一个相同的数（0除外）比值不变，进而把比化成最简比．【规范解答】解：（1）8：36＝（8÷4）：（36÷4）＝2：9 （2）0.25：0.5＝（0.25×4）：（0.5×4）＝1：2 （3）：＝（×4）：（×4）＝1：3【考点评析】此题主要考查了化简比的方法，另外还要注意化简比的结果是一个比，它的前项和后项都是整数，并且是互质数；而求比值的结果是一个商，可以是整数、小数或分数．15．求比值．14：0.72：13：27：0.2412.6：0.4：1【思路点拨】求比值是根据比的意义（两个数相除又叫两个数的比），用比的前项除以比的后项．【规范解答】解：：0.72＝14.4÷0.72＝20：＝÷＝：＝÷＝÷＝：0.24＝7.2÷0.24＝3012.6：0.4＝12.6÷0.4＝31.5：＝÷＝【考点评析】求比值是用比的前项除以后项，分数化成小数进行计算，结果可以是分数，小数和整数．五．应用题16．（2023•滨州模拟）图书室原来女生人数占总人数的40%，后来又进来8名女生，这时女生人数和总人数的比是6：13。图书室有多少名男生？【思路点拨】原来女生人数占男生人数的40%÷（1﹣40%），又进来8名女生后，女生人数占男生人数的÷（1﹣）。男生人数没变，看作单位“1”，根据分数除法的意义，用又进来的女生人数除以女生人数先后所占男生人数分率之差，就是图书室男生人数。【规范解答】解：8÷[÷（1﹣）﹣40%÷（1﹣40%）]＝8÷[÷﹣40%÷60%]＝8÷[﹣]＝8÷＝42（名）答：图书室有42名男生。【考点评析】解答此题的关键是抓住男生人数没变，看作单位“1”，分别求出女生人数先、后各占男生人数的几分之几（这也是难点），进而求出分率差，然后再根据分数除法的意义解答。17．（2022•兴平市）实验小学要对学校的餐具进行消毒，用84消毒液与水按1：9的质量比配制，一瓶1.2千克的消毒液需要加水多少千克？【思路点拨】1：9是消毒液与水的比。设一瓶1.2千克的消毒液需要加水x千克，所以1.2千克的消毒液：x＝1：9，据此列出比例计算即可。【规范解答】解：设一瓶1.2千克的消毒液需要加水x千克。1.2：x＝1：9       x＝1.2×9       x＝10.8答：一瓶1.2千克的消毒液需要加水10.8千克。【考点评析】本题考查了比的意义，关键是理解用消毒液：x＝1：9。18．（2021•阳谷县）山东凤祥集团是国家重点龙头企业。春节期间，华联、大润发、家乐福三家超市共购进凤祥五更炉熏鸡2400箱，其中华联超市购进的和其他两家的比是5：11，大润发购进的和其他两家的比是7：17。家乐福购进五更炉熏鸡多少箱？【思路点拨】总箱数看作单位“1”，则华联超市购进的箱数占，大润发购进的占总箱数的，家乐福购进了总箱数的（1﹣﹣），根据盆数乘法的意义，用总箱数乘（1﹣﹣）就是家乐福购进的箱数。【规范解答】解：2400×（1﹣﹣）＝2400×（1﹣﹣）＝2400×＝950（箱）答：家乐福购进五更炉熏鸡950箱。【考点评析】此题考查了比的应用。关键是把比转化成分数，进而求出家乐福购进的箱数所占的分率，然后根据分数乘法的意义解答。19．（2021•岚皋县）花店的李叔叔给某广场运了三天的盆花，第一天运了300盆，第一天与第二天运的盆花的盆数之比是5：4，第三天运了总盆数的25%，李叔叔这三天一共运了多少盆花？【思路点拨】先把第一天运的盆数看作单位“1”，则第二天运的盆数相当于第一天的，根据分数乘法的意义，用第一天运的盆数乘就是第二天运的盆数。再把三天运的总盆数看作单位“1”，前两天运的盆数之和正好占总盆数的（1﹣25%），根据百盆数除法的意义，用前两天运的盆数之和除以（1﹣25%）就是三运的总盆数。【规范解答】解：（300+300×）÷（1﹣25%）＝（300+240）÷75%＝540÷75%＝720（盆）答：李叔叔这三天一共运了720盆花。【考点评析】关键是把比转化成盆数，根据盆数乘法的意义求出第二天运的盆数，进而求出前两天运的盆数，然后再根据百分数除法的意义解答。20．（2022•德江县）慧慧家有一根长720厘米的铁条和一些铁皮，准备用这根铁条焊接成一个长方体框架并加工成养花盆。家里在讨论时，爸爸说：按长宽高的比为3：2：1焊接框架好看，慧慧说：按长宽高的比为3：2：2焊接框架好看，妈妈说：不能浪费铁条，而且为了不让花盆氧化需要在里外都刷上油漆，慧慧说：我想在花盆里放一个最大的圆柱玻璃鱼缸养鱼。你觉得她们家的花盆要刷多少面积的铁皮？最多还能装多少泥土？【思路点拨】首先求出长方体框架长、宽、高的和，再确定按哪种比分配能使长、宽、高都是整数；花盆在里外都刷上油漆，就是求长方体四个侧面与一个底面的面积和的2倍；用长方体花盆的体积减去以长方形的宽为直径且与长方体等高的圆柱的体积。【规范解答】解：720÷4＝180（厘米）若按长、宽、高的比为3：2：1，则将180厘米平均分成6份，180是6的倍数，长、宽、高都是整数。若按长、宽、高的比为3：2：2，则将180厘米平均分成7份，180不是7的倍数，长、宽、高都不是整数。所以应该按长、宽、高的比为3：2：1确定长、宽、高。长：180×＝90（厘米）宽：180×＝60（厘米）高：180×＝30（厘米）长方体框架包铁皮的面积：90×60+90×30×2+60×30×2＝14400（平方厘米）刷油漆的面积：14400×2＝28800（平方厘米）长方体花盆的体积：90×60×30＝162000（立方厘米）圆柱玻璃鱼缸的体积：3.14×（60÷2）2×30＝84780（立方厘米）能装泥土的面积：162000﹣84780＝77220（立方厘米）答：花盆要刷28800平方厘米的铁皮，最多还能装77220立方厘米的泥土。【考点评析】本题考查了按比例分配、长方体的棱长和、长方体的表面积、长方体的体积、圆柱体的体积，综合性强，需认真分析和解答。21．（2021•西安）在5月22日青海、云南发生地震后，某伞厂为支援地震灾区赶产一批帐篷，第一天生产了总帐篷数的20%，第一天与第二天生产的帐篷顶数比是5：7，还剩78顶帐篷没有生产，这批帐篷一共有多少顶？【思路点拨】把第一天生产的帐篷顶数看作5份，已知第一天生产了总帐篷数的20%，用20%÷5，求出一份占总帐篷数的百分之几，再用一份占总帐篷数的百分之几乘7，求出第二天生产了总帐篷数的百分之几，再用单位“1”分别减去第一天、第二天占的百分数，求出剩下的78顶占总帐篷数的百分之几，然后用78除以78顶占总帐篷数的百分数即可解答。【规范解答】解：20%÷5×7＝4%×7＝28%78÷（1﹣20%﹣28%）＝78÷52%＝150（顶）答：这批帐篷一共有150顶。【考点评析】本题考查了比较复杂的百分数问题和比的问题。关键是求出剩下的78顶占总帐篷数的百分之几。22．（2021•周至县）某校买来一些盆花布置校园，这些盆花的布置花坛，其余的按5：3布置教学楼和食堂，已知布置教学楼的有150盆花，学校一共买了多少盆花？【思路点拨】因为布置教学楼的有150盆花，布置教学楼和食堂的盆数比为5：3，则布置教学楼占布置教学楼和食堂的总盆数的，所以用布置教学楼的盆数除以求出布置教学楼和食堂的总盆数，又知道布置教学楼和食堂的总盆数占学校买来盆数的（1﹣），所以用布置教学楼和食堂的总盆数除以（1﹣）即可得学校一共买了多少盆花。【规范解答】解：150÷÷（1﹣）＝30×8÷＝640（盆）答：学校一共买了640盆花。【考点评析】本题主要考查了百分数的实际应用，已知一个数的百分之几是多少，求这个数，用除法计算。23．（2021•陈仓区）一块长方形耕地，长和宽的比是5：3，又知宽比长少40米，这块耕地的面积是多少平方米？【思路点拨】根据“长和宽的比是5：3”可知：长是5份，宽占3份，则宽比长少5﹣3＝2份，是40米，用40除以2即可求出每一份的长度，进而用每一份的长度乘各自所占的份数求出长与宽的长度，再根据长方形面积＝长×宽即可计算出面积．【规范解答】解：40÷（5﹣3）＝40÷2＝20（米）（20×5）×（20×3）＝100×60＝6000（平方米）．答：这块耕地的面积是6000平方米．【考点评析】解题关键是根据比的意义计算出多出的40米所占的份数，用除法求出每一份的长度，进而求出长与宽．24．（2021•敦化市）学校买来15箱彩笔，每箱12盒，按2：3分给五、六年级学生使用，每个年级各分到多少盒？【思路点拨】首先求出买来彩笔的总盒数，再求五、六年级分到的盒数分别占总盒数的几分之几，最后求出每个年级分到的盒数，列式解答即可．【规范解答】解：2+3＝512×15＝180（盒）180×＝72（盒）180×＝108（盒）答：五年级分到72盒，六年级分到108盒．【考点评析】此题主要考查按比例分配应用题的特点：已知两个数的比（三个数的比），两个数的和（三个数的和），求这两个数（三个数），用按比例分配解答．25．（2021•沂水县）水是由氢和氧按1：8的质量比化合而成的，540kg水含氢和氧各多少？【思路点拨】已知水是由氢和氧按1：8的质量比化合而成的，由此可知：氢占水质量的，氧占水质量的，把水的质量看作单位“1”，根据一个数乘分数的意义，用乘法解答．【规范解答】解：540×＝＝60（千克） 540×＝＝480（千克）答：540千克水含氢60千克、含氧480千克．【考点评析】此题考查的目的是理解掌握比的意义及应用，以及按比例分配的实际应用．26．（2020•大邑县）甲、乙两个水果店，乙水果店原有水果800千克．当甲水果店销售掉，乙水果店销售掉80%后，乙店剩下的水果重量与甲、乙两个店剩下水果的重量总数之比为2：7，甲店原有水果多少千克？（解答题，写出主要解答步骤）【思路点拨】首先把乙水果店有水果的质量看作单位“1”，乙水果店销售掉80%后，乙还剩下总数的（1﹣80%），根据一个数乘百分数的意义，用乘法求出乙水果店还剩下水果多少千克．当甲水果店销售掉，乙店剩下的水果重量与甲、乙两个店剩下水果的重量总数之比为2：7，也就是乙水果店剩下水果的质量占甲、乙两个店剩下水果的重量总数，再根据已知一个数的几分之几是多少，求这个数，用除法求出甲、乙两个店剩下水果的重量总数，进而求出甲水果店原有水果多少千克．【规范解答】解：800×（1﹣80%）÷×÷（1）＝800×0.2÷＝＝400×＝1400（千克），答：甲店原有水果1400千克．【考点评析】此题考查的目的是理解掌握比的意义，比与分数之间的联系及应用，关键是确定单位“1”．